
- •II. Число (число Эйлера, число Непера)
- •Необходимое условие сходимости ряда.
- •Достаточные признаки сходимости знакоположительного ряда.
- •Первый, второй и третий признаки сравнения.
- •Признак Даламбера.
- •Радикальный признак Коши.
- •Интегральный признак Коши.
- •Признак Раабе.
- •Исследование знакопеременных рядов на абсолютную сходимость.
- •Следствие
Определения модуля, интервала, отрезка, окрестности, открытого и закрытого множества
Модуль (абсолютная величина) действительного числа Х – само число Х, если Х неотрицательно, и противоположное число –Х, если оно отрицательно.
Интервал (геометрия) — множество точек прямой, заключённых между точками А и В, причём сами точки А и В не причисляются к интервалу, иначе говорят об отрезке;
Интервал числовой оси — множество чисел, заключённых в некоторых границах (возможно, бесконечных).
Окре́стность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней. Множество значений, удаленных от Х не более чем на некое значение эпсилон.
Открытое/закрытое множество - Откры́тое мно́жество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии. За́мкнутые мно́жества в общей топологии, функциональном анализе и математическом анализе — это дополнения к открытым множествам. Замкнутое множество содержит все свои точки прикосновения.
Ограниченные множества. Понятия супремума и инфинума.
Ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общих топологических пространствах, без метрики.
Множество А называептся ограниченным сверху, если существует число Бэ, которое более всех чисел-элементов множества А. В этом случае Бэ – верхняя граница. А Точная Верхняя Граница множества А – это наименьшая из верхних границ, которая обозначается супремум А.
Точная Нижняя Граница – наибольшая из нижних границ. Это инфинум А.
Уравнения прямой на плоскости
Y = kx +b
K = (y – b)/x – угловой коэффициент прямой, равный tgA
Уравнение прямой, проходящей через данную точку в данном направлении:
(прямая проходит через точку М(х1, у1), угол с осью Ох не равен 90градусов)
У-у1=к(х-х1)
Если прямая проходит через точку М, и имеет произвольные коэффициент к, то мы говорим о пучке прямых.
Уравнение прямой, проходящей через две точки М1(х1, у1) и М2(х2, у2):
К = (у2-у1)/(х2-х1)
(у-у1)/(у2-у1) = (х-х1)/(х2-х1)
Уравнение прямой в отрезках:
х/а + у/б = 1, где а и б – заданные отрезки, не равные нулю.
Парабола и ее график
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Квадратное уравнение
ах-кв + бх +с = 0 при а не равном нулю также
представляет собой параболу и графически
изображается той же параболой, что и у
= ах-кв , но в отличие от последней имеет
вершину не в начале координат, а в
некоторой точке , координаты которой
вычисляются по формулам:
![]()
где
![]() — дискриминант
— дискриминант
Ось её симметрии проходит через вершину параллельно оси ординат, при a>0 (a<0) фокус лежит на этой оси над (под) вершиной на расстоянии a/4, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение может быть представлено в виде , а в случае переноса начала координат в точку каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим.
ГРАФИКИ ФУНКЦИЙ (ЭЛЕМЕНТАРНЫХ; ВСЕХ)
Степенная
функция, ее график и свойства.
![]()
Показательная
функция, свойства, график.
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]()
Логарифмическая
функция, ее свойства, графическая
иллюстрация.
![]() ,
где
,
и
,
где
,
и
![]()
Свойства
и графики тригонометрических функций.
![]()
Обратные
тригонометрические функции (аркфункции),
их свойства и графики.
![]()
Степенная функция.
ЗАМЕЧАНИЯ:
к основным элементарным степенным функциям относят лишь степенную функцию С ЦЕЛЫМ ПОКАЗАТЕЛЕМ, однако мы рассмотрим все возможные действительные значения показателя степени для общего представления;
некоторые авторы при рассмотрении степенной функции ограничивают область определения интервалом . Мы же не будем придерживаться этого ограничения. Рекомендем уточнить отношение Вашего преподавателя к этому вопросу во избежании недоразумений. В любом случае все изложенное будет верно (если при области определения рассматривать только этот интервал и отбрасывать все оставшиеся).
Рассмотрим вид и свойства степенной функции в зависимости от значения показателя степени (17 вариантов показателя степени: четный положительный, четный отрицательный, нечетный положительный, нечетный отрицательный, иррациональный, масса вариантов дробно рационального показателя).
Степенная функция с нечетным положительным показателем.
Рассмотрим степенную функцию при нечетном положительном показателе степени, то есть, а = 1, 3, 5, ….
На рисунке ниже
приведены графики степенных фнукций
![]() –
черная линия,
–
черная линия,
![]() –
синяя линия,
–
синяя линия,
![]() –
красная линия,
–
красная линия,
![]() –
зеленая линия. При а = 1 имеем
линейную функцию y = x -
частный случай степенной.
–
зеленая линия. При а = 1 имеем
линейную функцию y = x -
частный случай степенной.

Свойства степенной функции с нечетным положительным показателем.
Область определения: .
Область
значений:
![]() .
.
Функция
нечетная, так как
![]() .
.
Функция возрастает при .
Функция
выпуклая при
![]() и
вогнутая при
и
вогнутая при
![]() (кроме
линейной функции).
(кроме
линейной функции).
Точка (0;0) является точкой перегиба (кроме линейной функции).
Асимптот нет.
Функция проходит через точки (-1;-1), (0;0), (1;1).
К началу страницы
Степенная функция с нечетным отрицательным показателем.
Посмотрите на графики степенной функции при нечетных отрицательных значениях показателя степени, то есть, при а = -1, -3, -5, …
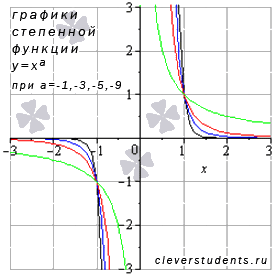
На рисунке в качестве
примеров показаны графики степенных
функций
![]() –
черная линия,
–
черная линия,
![]() –
синяя линия,
–
синяя линия,
![]() –
красная линия,
–
красная линия,
![]() –
зеленая линия. При а = -1 имеем
обратную пропорциональность
(гиперболу) - частный случай степенной
функции.
–
зеленая линия. При а = -1 имеем
обратную пропорциональность
(гиперболу) - частный случай степенной
функции.
Свойства степенной функции с нечетным отрицательным показателем.
Область
определения:
![]() .
При
x = 0
имеем разрыв второго рода, так как
.
При
x = 0
имеем разрыв второго рода, так как
![]() при
а = -1, -3, -5, ….
Следовательно, прямая x
= 0 является вертикальной
асимптотой.
при
а = -1, -3, -5, ….
Следовательно, прямая x
= 0 является вертикальной
асимптотой.
Область
значений:
![]() .
.
Функция нечетная, так как .
Функция убывает при .
Функция
выпуклая при
![]() и
вогнутая при
.
и
вогнутая при
.
Точек перегиба нет.
Горизонтальной
асимптотой является прямая y
= 0, так как
 при
а = -1, -3, -5, ….
при
а = -1, -3, -5, ….
Функция проходит через точки (-1;-1), (1;1).
К началу страницы
Степенная функция с четным положительным показателем.
Рассмотрим степенную функцию с четным положительным показателем степени, то есть, при а = 2, 4, 6, ….
В качестве примера
приведем графики степенных функций
![]() –
черная линия,
–
черная линия,
![]() –
синяя линия,
–
синяя линия,
![]() –
красная линия. При а = 2 имеем
квадратичную функцию – квадратичную
параболу – частный случай степенной
функции.
–
красная линия. При а = 2 имеем
квадратичную функцию – квадратичную
параболу – частный случай степенной
функции.
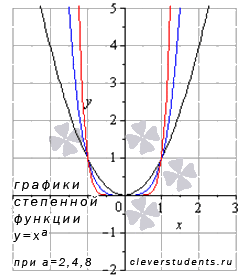
Свойства степенной функции с четным положительным показателем.
Область определения: .
Область
значений:
![]() .
.
Функция
четная, так как
![]() .
.
Функция возрастает при , убывает при .
Функция вогнутая при .
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (-1;1), (0;0), (1;1).
К началу страницы
Степенная функция с четным отрицательным показателем.
Перейдем к степенной функции при а = -2, -4, -6, …

На рисунке изображены
графики степенных функций
![]() –
черная линия,
–
черная линия,
![]() –
синяя линия,
–
синяя линия,
![]() –
красная линия.
–
красная линия.
Свойства степенной функции с четным отрицательным показателем.
Область
определения:
.
При
x = 0
имеем разрыв второго рода, так как
![]() при
а = -2, -4, -6, ….
Следовательно, прямая x = 0
является вертикальной асимптотой.
при
а = -2, -4, -6, ….
Следовательно, прямая x = 0
является вертикальной асимптотой.
Область
значений:
![]() .
.
Функция четная, так как .
Функция возрастает при , убывает при .
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0, так как при а=-2, -4, -6, ….
Функция проходит через точки (-1;1), (1;1).
К началу страницы
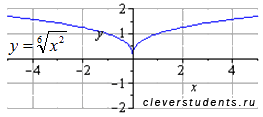
Степенная функция с рациональным показателем.
Рассмотрим графики
степенной функции
,
если
![]() и
а – несократимая рациональная дробь
с четным знаменателем (например, а = 1/4
или 3/8). (Про важность несократимости
рациональной дроби написано в замечании
к этому пункту).
и
а – несократимая рациональная дробь
с четным знаменателем (например, а = 1/4
или 3/8). (Про важность несократимости
рациональной дроби написано в замечании
к этому пункту).

На рисунке в качестве
примера показаны графики степенных
функций
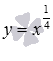 –
черная линия,
–
черная линия,
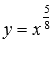 –
синяя линия,
–
синяя линия,
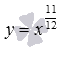 –
красная линия.
–
красная линия.
Свойства степенной функции с положительным рациональным показателем меньшим единицы.
Область определения: .
Область значений: .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при .
Функция выпуклая при .
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (0;0), (1;1).
Замечание.
Если
и
а – иррациональное число (например,
![]() ),
то вид графика степенной функции
аналогичен виду графиков, изображенных
в этом пункте, свойства степенной функции
с иррациональным показателем абсолютно
схожи.
),
то вид графика степенной функции
аналогичен виду графиков, изображенных
в этом пункте, свойства степенной функции
с иррациональным показателем абсолютно
схожи.
Замечание о важности несократимости рациональной дроби в показателе степени.
Не поймите нас
неправильно. Здесь мы проводим тонкую
грань. Она заключается в том, что графики
функций
 и
и
 не
совпадают, если не оговорен момент о
несократимости показателя степени.
Этим мы НЕ ХОТИМ сказать, что
не
совпадают, если не оговорен момент о
несократимости показателя степени.
Этим мы НЕ ХОТИМ сказать, что
![]() ,
но графики функций
,
но графики функций
 и
и
![]() не
соответствуют графику степенной функции
.
не
соответствуют графику степенной функции
.
Вот тому графическая иллюстрация:

В дальнейшем
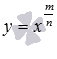 будем
рассматривать как
будем
рассматривать как
![]()
К началу страницы
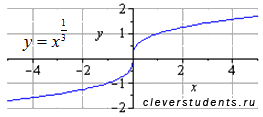
Рассмотрим степенную функцию когда , а также числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, причем сама дробь несократима (например, 1/3 или 5/7).
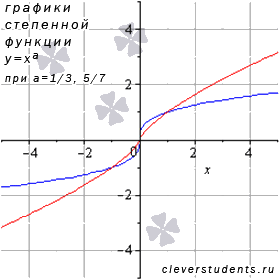
На рисунке представлены
графики степенных функций
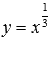 –
синяя линия,
–
синяя линия,
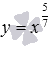 –
красная линия.
–
красная линия.
Свойства степенной функции с положительным рациональным показателем меньшим единицы.
Область определения: .
Область значений: .
Функция нечетная, так как .
Функция возрастает при .
Функция вогнутая при и выпуклая при .
Точка (0;0) является точкой перегиба.
Асимптот нет.
Функция проходит через точки (-1;-1), (0;0), (1;1).
К началу страницы
Сейчас остановимся на степенной функции , у которой и числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число и сама дробь несократима (например, 2/3 или 6/7).
Графики степенной
функции
при
а = 2/5 и а = 6/7 имеют вид
(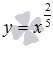 – синяя линия,
– синяя линия,
 –
красная линия):
–
красная линия):
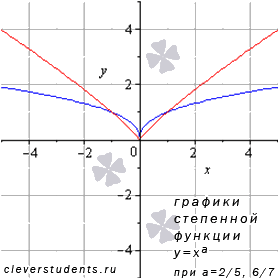
Свойства степенной функции для этого случая.
Область определения: .
Область значений: .
Функция четная, так как .
Функция возрастает при , убывает при .
Функция выпуклая при .
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (-1;1), (0;0), (1;1).
К началу страницы
Рассмотрим степенную
функцию
,
когда
![]() и
а – несократимая рациональная дробь
с четным знаменателем (например, а = 7/4
или 11/8).
и
а – несократимая рациональная дробь
с четным знаменателем (например, а = 7/4
или 11/8).

В качестве примера
на рисунке изображены графики степенных
функций
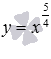 –
черная линия,
–
черная линия,
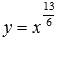 –
красная линия,
–
красная линия,
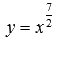 –
синяя линия.
–
синяя линия.
Свойства степенной функции с положительным рациональным показателем большим единицы.
Область определения: .
Область значений: .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при .
Функция
вогнутая при
,
если
![]() ;
при
,
если
;
при
,
если
![]() .
.
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (0;0), (1;1).
Замечание.
Если и а – иррациональное число (например, корень четвертой степени из 19,23), то вид графика степенной функции с иррациональным показателем аналогичен виду графиков, показанных в этом пункте, свойства абсолютно схожи.
К началу страницы
Перейдем к степенной функции, когда , а числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, причем сама дробь несократима (например, 7/3 или 25/7).
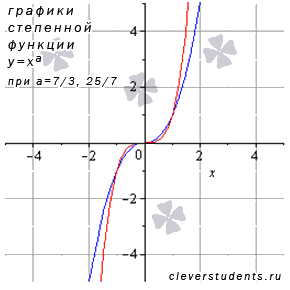
В качестве примера
приведены графики степенных функций
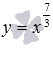 –
синяя линия,
–
синяя линия,
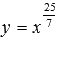 –
красная линия.
–
красная линия.
Свойства степенной функции с положительным рациональным показателем большим единицы.
Область определения: .
Область значений: .
Функция нечетная, так как .
Функция возрастает при .
Функция вогнутая при и выпуклая при .
Точка (0;0) является точкой перегиба.
Асимптот нет.
Функция проходит через точки (-1;-1), (0;0), (1;1).
К началу страницы
Разберемся со степенной функцией, если и числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число, а сама дробь несократима (например, 8/3 или 16/7).
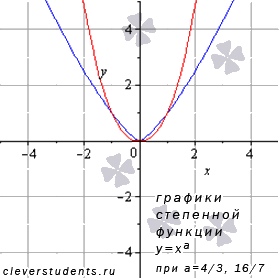
На рисунке изображены
графики степенных функций
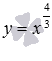 –
синяя линия,
–
синяя линия,
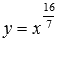 –
красная линия.
–
красная линия.
Свойства степенной функции с положительным рациональным показателем большим единицы.
Область определения: .
Область значений: .
Функция четная, так как .
Функция возрастает при , убывает при .
Функция вогнутая при .
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (-1;1), (0;0), (1;1).
К началу страницы
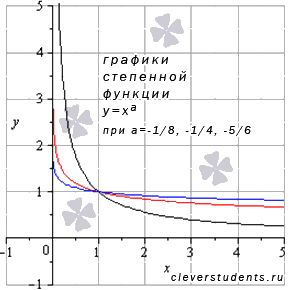
Рассмотрим степенную
функцию
для
случая, когда
![]() и
а – несократимая рациональная дробь
с четным знаменателем (например, а = -1/2
или -5/8).
и
а – несократимая рациональная дробь
с четным знаменателем (например, а = -1/2
или -5/8).
Для наглядности
приведем графики степенных функций
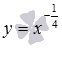 –
красная линия,
–
красная линия,
 –
синяя линия,
–
синяя линия,
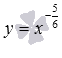 –
черная линия.
–
черная линия.
Свойства степенной функции с отрицательным рациональным показателем.
Область определения:
.
Поведение
на границе области определения
![]() при
и
а – рациональная дробь. Следовательно,
х = 0 является вертикальной
асимптотой.
при
и
а – рациональная дробь. Следовательно,
х = 0 является вертикальной
асимптотой.
Область значений: .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция убывает при .
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точку (1;1).
Замечание.
Если и а – иррациональное число (например, минус корень четвертой степени из 0,21), то для этого случая вид графика степенной функции аналогичен виду графиков, рассмотренных в этом пункте, свойства такой степенной функции совпадают со свойствами, перечисленными выше.
К началу страницы
Переходим к степенной функции , кгода а числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, причем сама дробь несократима (к примеру, -1/3 или -5/7).
В качестве примера
построены графики степенных функций
 –
синяя линия,
–
синяя линия,
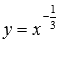 –
красная линия.
–
красная линия.
Свойства степенной функции с отрицательным рациональным показателем.
Область определения: . Поведение на границе области определения при и а – несократимая рациональная дробь с нечетным числителем и знаменателем. Следовательно, х = 0 является вертикальной асимптотой.
Область значений: .
Функция нечетная, так как .
Функция убывает при .
Функция выпуклая при и вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точки (-1;-1), (1;1).
К началу страницы
Сейчас поговорим о степенной функции , если и если числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число, а сама дробь несократима (например, -2/3 или -6/7).
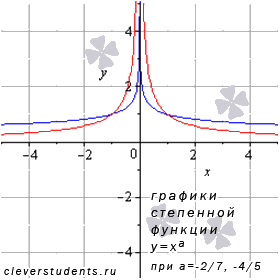
На рисунке показаны
графики степенных функций
 –
синяя линия,
–
синяя линия,
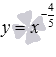 –
красная линия.
–
красная линия.
Свойства степенной функции с отрицательным рациональным показателем.
Область определения: . Поведение на границе области определения при и а – несократимая рациональная дробь с четным числителем и нечетным знаменателем. Следовательно, х = 0 является вертикальной асимптотой.
Область значений: .
Функция четная, так как .
Функция возрастает при , убывает при .
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точки (-1;1), (1;1).
К началу страницы
Переходим к степенной
функции
для
случая, когда
![]() и
а – несократимая рациональная дробь
с четным знаменателем (например, а = -3/2
или -21/8).
и
а – несократимая рациональная дробь
с четным знаменателем (например, а = -3/2
или -21/8).
Для примера покажем
графики степенных функций
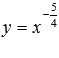 –
красная линия,
–
красная линия,
 –
синяя линия и
–
синяя линия и
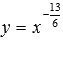 –
черная линия.
–
черная линия.
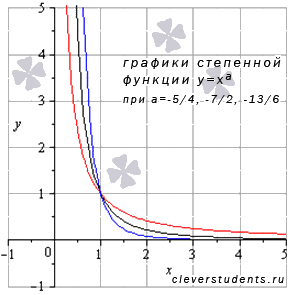
Свойства степенной функции с отрицательным рациональным показателем.
Область определения: . Поведение на границе области определения при и а – рациональная дробь с четным знаменателем. Следовательно, х = 0 является вертикальной асимптотой.
Область значений: .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция убывает при .
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точку (1;1).
Замечание.
Если и а – иррациональное число (например, минус корень квадратный из семи), то вид графика такой степенной функции аналогичен виду графиков, показанных в этом пункте, свойства абсолютно схожи.
К началу страницы
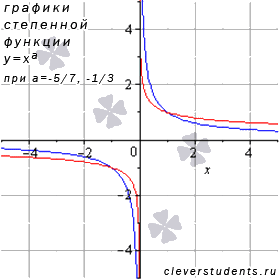
Рассмотрим степенную функцию , когда , числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, а сама дробь несократима (к примеру, -5/3 или -25/7).
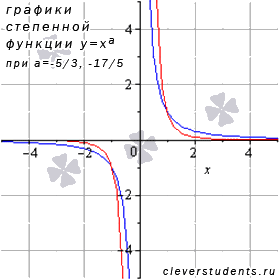
В качестве примера
на рисунке изображены графики степенных
функци
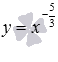 –
синяя линия,
–
синяя линия,
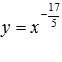 –
красная линия.
–
красная линия.
Свойства степенной функции с отрицательным рациональным показателем.
Область определения: . Поведение на границе области определения при и а – несократимая рациональная дробь с нечетным и числителем и знаменателем. Следовательно, х = 0 является вертикальной асимптотой.
Область значений: .
Функция нечетная, так как .
Функция убывает при .
Функция выпуклая при и вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точки (-1;-1), (1;1).
К началу страницы
Разберемся со степенной функцией , когда , числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число и сама дробь несократима (например, -6/5 или -24/7).
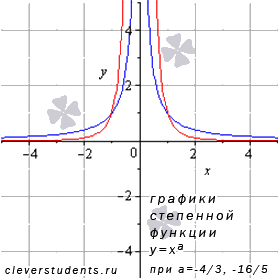
На иллюстрации взяты
графики степенных функций
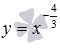 –
синяя линия,
–
синяя линия,
 –
красная линия.
–
красная линия.
Свойства степенной функции с отрицательным рациональным показателем.
Область определения: . Поведение на границе области определения при и а – несократимая рациональная дробь с четным числителем и нечетным знаменателем. Следовательно, х = 0 является вертикальной асимптотой.
Область значений: .
Функция четная, так как .
Функция возрастает при , убывает при .
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точки (-1;1), (1;1).
К началу страницы
При а = 0 и
![]() имеем
функцию
имеем
функцию
![]() -
это прямая из которой исключена точка
(0;1). При а = 0 и х = 0
условимся не придавать функции никакого
числового значения.
-
это прямая из которой исключена точка
(0;1). При а = 0 и х = 0
условимся не придавать функции никакого
числового значения.
К началу страницы
Показательная функция.
Одной из основных элементарных функций является показательная функция.
График показательной функции , где и принимает различный вид в зависимости от значения основания а. Разберемся в этим.
Сначала рассмотрим случай, когда основание показательной функции принимает значение от нуля до единицы, то есть, .
Для примера приведем графики показательной функции при а = 1/2 – синяя линия, a = 5/6 – красная линия. Аналогичный вид имеют графики показательной функции при других значениях основания из интервала .
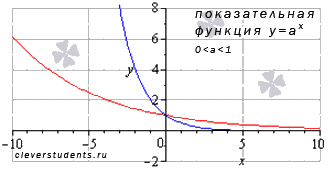
Свойства показательной функции с основанием меньшим единицы.
Областью определения показательной функции является все множество действительнйх чисел: .
Область значений: .
Функция не является ни четной, ни нечетной, то есть, она общего вида.
Показательная функция, основание которой меньше единицы, убывает на всей области определения.
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0 при х стремящемся к плюс бесконечности.
Функция проходит через точку (0;1).
К началу страницы
Переходим к случаю, когда основание показательной функции больше единицы, то есть, .
В качестве иллюстрации
приведем графики показательных функций
 –
синяя линия и
–
синяя линия и
![]() –
красная линия. При других значениях
основания, больших единицы, графики
показательной функции будут иметь
схожий вид.
–
красная линия. При других значениях
основания, больших единицы, графики
показательной функции будут иметь
схожий вид.

Свойства показательной функции с основанием большим единицы.
Область определения показательной функции: .
Область значений: .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Показательная функция, основание которой больше единицы, возрастает при .
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0 при х стремящемся к минус бесконечности.
Функция проходит через точку (0;1).
К началу страницы
Логарифмическая функция.
Следующей основной элементарной функцией является логарифмическая функция , где , . Логарифмическая функция определена лишь для положительных значений аргумента, то есть, при .
График логарифмической функции принимает различный вид в зависимости от значения основания а.
Начнем со случая, когда .
Для примера приведем графики логарифмической функции при а = 1/2 – синяя линия, a = 5/6 – красная линия. При других значениях основания, не превосходящих единицы, графики логарифмической функции будут иметь схожий вид.

Свойства логарифмической функции с основанием меньшим единицы.
Область определения логарифмической функции: . При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
Область значений: .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Логарифмическая функция убывает на всей области определения.
Функция вогнутая при .
Точек перегиба нет.
Горизонтальных асимптот нет.
Функция проходит через точку (1;0).
К началу страницы
Перейдем к случаю, когда основание логарифмической функции больше единицы ( ).
Покажем графики
логарифмических функций
 –
синяя линия,
–
синяя линия,
![]() –
красная линия. При других значениях
основания, больших единицы, графики
логарифмической функции будут иметь
схожий вид.
–
красная линия. При других значениях
основания, больших единицы, графики
логарифмической функции будут иметь
схожий вид.
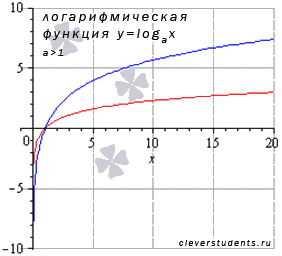
Свойства логарифмической функции с основанием большим единицы.
Область определения: . При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности.
Областю значений логарифмической функции является все множество действительных чисел, то есть, интервал .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при .
Функция выпуклая при .
Точек перегиба нет.
Горизонтальных асимптот нет.
Функция проходит через точку (1;0).
К началу страницы
Тригонометрические функции, их свойства и графики.
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим
функциям присуще понятие периодичности
(повторяемости значений функции при
различных значениях аргумента, отличных
друг от друга на величину периода
![]() ,
где Т - период), поэтому, в список
свойств тригонометрических функций
добавлен пункт «наименьший положительный
период». Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.
,
где Т - период), поэтому, в список
свойств тригонометрических функций
добавлен пункт «наименьший положительный
период». Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Функция синус y = sin(x).
Изобразим график функции синус, его называют "синусоида".
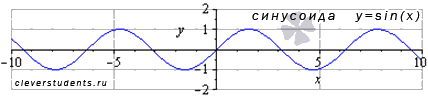
Свойства функции синус y = sinx.
Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
Наименьший положительный
период функции синуса равен двум пи:
![]() .
.
Функция обращается
в ноль при
![]() ,
где
,
где
![]() ,
Z – множество целых чисел.
,
Z – множество целых чисел.
Функция синус принимает
значения из интервала от минус единицы
до единицы включительно, то есть, ее
область значений есть
![]() .
.
Функция синус - нечетная, так как .
Функция убывает при
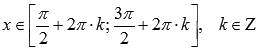 ,
возрастает
при
,
возрастает
при
![]() .
.
Функция синус имеет
локальные максимумы в точках
![]() ,
локальные
минимумы в точках
,
локальные
минимумы в точках
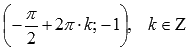 .
.
Функция y = sinx
вогнутая при
![]() ,
выпуклая
при
,
выпуклая
при
![]() .
.
Координаты точек
перегиба
![]() .
.
Асимптот нет.
К началу страницы
Функция косинус y = cos(x).
График функции косинус (его называют "косинусоида") имеет вид:
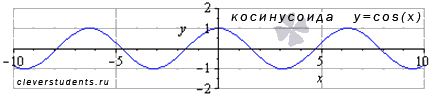
Свойства функции косинус y = cosx.
Область определения функции косинус: .
Наименьший положительный период функции y = cosx равен двум пи: .
Функция обращается
в ноль при
![]() ,
где
,
Z – множество целых чисел.
,
где
,
Z – множество целых чисел.
Область значений функции косинус представляет интервал от минус единицы до единицы включительно: .
Функция косинус - четная, так как .
Функция убывает при , возрастает при .
Функция y = cosx
имеет локальные максимумы в точках
![]() ,
локальные
минимумы в точках
,
локальные
минимумы в точках
![]() .
.
Функция вогнутая при , выпуклая при .
Координаты точек
перегиба
![]() .
.
Асимптот нет.
К началу страницы
Функция тангенс y = tg(x).
График функции тангенс (его называют "тангенсоида") имеет вид:
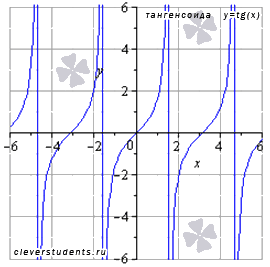
Свойства функции тангенс y = tgx.
Область определения
функции тангенс:
![]() ,
где
,
Z – множество целых чисел.
Поведение
функции y = tgx на границе области
определения
,
где
,
Z – множество целых чисел.
Поведение
функции y = tgx на границе области
определения
![]() Следовательно,
прямые
,
где
,
являются вертикальными асимптотами.
Следовательно,
прямые
,
где
,
являются вертикальными асимптотами.
Наименьший положительный
период функции тангенс
![]() .
.
Функция обращается в ноль при , где , Z – множество целых чисел.
Область значений функции y = tgx: .
Функция тангенс - нечетная, так как .
Функция возрастает
при
![]() .
.
Функция вогнутая при
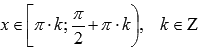 ,
выпуклая
при
,
выпуклая
при
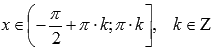 .
.
Координаты точек перегиба .
Наклонных и горизонтальных асимптот нет.
К началу страницы
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют "котангенсоида"):

Свойства функции котангенс y = ctgx.
Область определения
функции котангенс:
![]() ,
где
,
Z – множество целых чисел.
Поведение
на границе области определения
,
где
,
Z – множество целых чисел.
Поведение
на границе области определения
![]() Следовательно,
прямые
,
где
являются
вертикальными асимптотами.
Следовательно,
прямые
,
где
являются
вертикальными асимптотами.
Наименьший положительный период функции y = ctgx равен пи: .
Функция обращается в ноль при , где , Z – множество целых чисел.
Область значений функции котангенс: .
Функция нечетная, так как .
Функция y = ctgx
убывает при
![]() .
.
Функция котангенс
вогнутая при
![]() ,
выпуклая
при
,
выпуклая
при
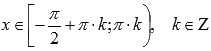 .
.
Координаты точек перегиба .
Наклонных и горизонтальных асимптот нет.
К началу страницы
Обратные тригонометрические функции, их свойства и графики.
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
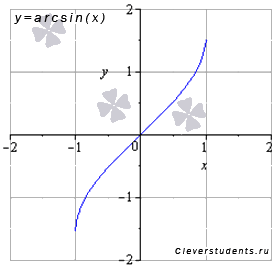
Свойства функции арксинус y = arcsin(x).
Областью определения
функции арксинус является интервал от
минус единицы до единицы включительно:
![]() .
.
Область значений
функции y = arcsin(x):
![]() .
.
Функция арксинус - нечетная, так как .
Функция y = arcsin(x) возрастает на всей области определения, то есть, при .
Функция вогнутая при
![]() ,
выпуклая при
,
выпуклая при
![]() .
.
Точка перегиба (0; 0), она же ноль функции.
Асимптот нет.
К началу страницы
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:

Свойства функции арккосинус y = arccos(x).
Область определения функции арккосинус: .
Область значений
функции y = arccos(x):
![]() .
.
Функция не является ни четной ни нечетной, то есть, она общего вида.
Функция арккосинус убывает на всей области определения, то есть, при .
Функция вогнутая при , выпуклая при .
Точка перегиба
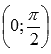 .
.
Асимптот нет.
К началу страницы
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
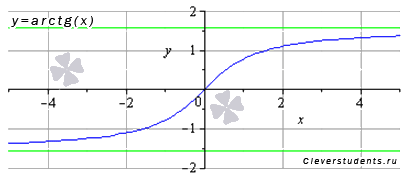
Свойства функции арктангенс y = arctg(x).
Область определения функции y = arctg(x): .
Область значений
функции арктангенс:
![]() .
.
Функция арктангенс - нечетная, так как .
Функция возрастает на всей области определения, то есть, при .
Функция арктангенс вогнутая при , выпуклая при .
Точка перегиба (0; 0), она же ноль функции.
Горизонтальными
асимптотами являются прямые
![]() при
при
![]() и
и
![]() при
при
![]() .
На чертеже они показаны зеленым цветом.
.
На чертеже они показаны зеленым цветом.
К началу страницы
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
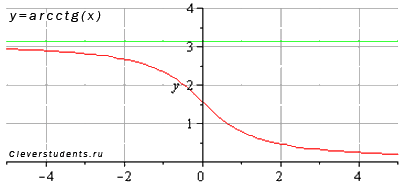
Свойства функции арккотангенс y = arcctg(x).
Областью определения функции арккотангенс является все множество действительных чисел: .
Область значений
функции y = arcctg(x):
![]() .
.
Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
Функция убывает на всей области определения, то есть, при .
Функция вогнутая при , выпуклая при .
Точка перегиба .
Горизонтальными
асимптотами являются прямые
![]() при
(на
чертеже показана зеленым цветом) и y = 0
при
.
при
(на
чертеже показана зеленым цветом) и y = 0
при
.
Построение графиков с модулем
Модуль функции у=|f(x)|
Из определения модуля числа следует метод построения.
Строим сначала график функции , затем точки графика, лежащие выше оси абсцисс, оставляем без изменения, а точки графика, лежащие под осью абсцисс, отражаем симметрично оси абсцисс.
11) Метод мат. Индукции и бином Ньютона.
В основе метода математической индукции лежит принцип математической индукции. Он заключается в следующем: утверждение справедливо для всякого натурального n, если
оно справедливо для n = 1 и
из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1.
То есть, доказательство по методу математической индукции проводится в три этапа:
во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1);
во-вторых, предполагается справедливость утверждения при любом натуральном n = k;
в-третьих, доказывается справедливость утверждения для числа n = k+1, отталкиваясь от предположения второго пункта.
Формула бинома Ньютона
имеет вид:
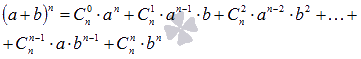 ,
где
,
где
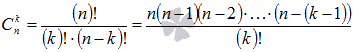 -
биномиальные коэффициенты, представляющие
собой сочетания. Квадрат суммы, например,
частный случай применения бинома Ньютона
.
-
биномиальные коэффициенты, представляющие
собой сочетания. Квадрат суммы, например,
частный случай применения бинома Ньютона
.
14) Последовательность и ее предел. Бесконечно малые/большие последовательности и их сравнение.
Последовательность — это набор элементов некоторого множества:
для каждого натурального числа можно указать элемент данного множества;
это число является номером элемента и обозначает позицию данного элемента в последовательности;
для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Число В называется пределом последовательности у1у2…ун, если по мере возрастания числа Н, уН неограниченно приближается к В.
Неограниченность приближения выражается в том, что абсолютная величина разницы уН-В, начиная с некоторого числа Н, остается меньше любого заранее заданного положительного числа эпсилон. Т.е. разница уН и В по модулю меньше эпсилона.
Число В называется пределом функции ф(х) при Х стремящемся к А, если абсолютное значение разности ф(х) и В по модулю меньше любого заранее заданного положительного числа эпсилон. Всякий раз, как абсолютное значение разницы х-а при х не равном а меньше некоторого числа сигма(эпсилон).
Пределом постоянной величины В является величина В.
Бесконечно малой величиной называется величина, предел которой равен нулю.
Х-квадрат – 4 при х, стремящемся к двум, является бесконечно малой величиной.
Бесконечно большой величиной называется переменная величина, абсолютное значение которой неограниченно возрастает. При х стремящемся к нулю – Большая, при х – к бесконечности – малая. Никакая постоянная величина не является бесконечно большой!
Величина называется ограниченной, если абсолютное ее значение не превосходит некоторого постоянного положительного числа Эн. Любая константа является ограниченной, а неограниченная величина не может быть бесконечно большой.
Сумма неизменного количества бесконечно малых величин есть БМВ. Разность двух БМВ есть БМВ.
Произведение ограниченной величины на БМВ, а также произведение двух БМВ есть БМВ.
Частное от деления БМВ на переменную величину есть БМВ.
Ни одно число, кроме нуля, не может быть отнесено к бесконечно малым величинам.
2. Алгебраическая сумма нескольких бесконечно малых величин есть также величина бесконечно малая.
Алгебраической суммой называется такая сумма, члены которой присоединяются друг к другу не только при помощи знака плюс, но и при помощи знака минус.
3. Разность двух бесконечно малых величин есть величина бесконечно малая.
4. Произведение ограниченной переменной величины на бесконечно малую есть величина бесконечно малая.
Отсюда следует:
а) Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.
б) Произведение переменной величины, стремящейся к пределу, на бесконечно малую есть величина бесконечно малая.
в) Произведение двух бесконечно малых величин есть величина бесконечно малая.
5. Отношение двух бесконечно малых величин не обязательно есть величина бесконечно малая.
Отношение двух бесконечно малых величин может быть величиной конечной, бесконечно малой и даже бесконечно большой величиной.
Об отношении двух бесконечно малых величин иногда говорят, что оно представляет собой "неопределенность" вида . ноль на ноль
Вычисление предела отношения двух бесконечно малых часто называется также раскрытием "неопределенности" вида . такого же
15) Встречные последовательности. Теорема о двух милиционерах.
Теорема о двух
милиционерах: лемма в математическом
анализе о существовании предела у
функции, которая «зажата» между двумя
другими функциями, имеющими одинаковый
предел. Формулируется следующим образом:
Если функция
![]() такая, что
такая, что
![]() для всех Х в некоторой окрестности
точки Альфа, причем функции фи(х) и пси(х)
имеют одинаковый предел, при Х,
стремящемся, к А, то существует предел
функции у = ф(х) при Х, стремящемся к А,
равный этому же значению, т.е.
для всех Х в некоторой окрестности
точки Альфа, причем функции фи(х) и пси(х)
имеют одинаковый предел, при Х,
стремящемся, к А, то существует предел
функции у = ф(х) при Х, стремящемся к А,
равный этому же значению, т.е.
![]()
17) Число е
e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».
Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.
Число e может быть определено несколькими способами.
Через предел
![]() (второй замечательный предел)
(второй замечательный предел)
Как сумма ряда
![]() или
или
![]()
Как единственное
число а, для которого выполняется:
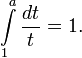
16) Предел монотонной
ограниченной последовательности.
Существование корня степени
![]() из
вещественного числа. Число
из
вещественного числа. Число
![]()
Определение. Пусть
![]() —
произвольная числовая последовательность.
Построим новую последовательность по
правилу
—
произвольная числовая последовательность.
Построим новую последовательность по
правилу
![]()
Последовательность
![]() называется
последовательностью частичных сумм
последовательности
.
называется
последовательностью частичных сумм
последовательности
.
Определение. Пусть — последовательность, — последовательность частичных сумм последовательности . Предел последовательности называется суммой всех членов последовательности .
Найдем сумму всех
членов бесконечно убывающей
геометрической прогрессии, т.е.
геометрической прогрессии со знаменателем,
по модулю меньшим
![]() .
.
Пусть
—
геометрическая прогрессия с первым
членом
![]() и
знаменателем
и
знаменателем
![]() .
.
![]() .
Действительно, из неравенства Бернулли
.
Действительно, из неравенства Бернулли
![]()
имеем
![]()
Поскольку
![]() ,
то
,
то
![]() представимо
в виде
представимо
в виде
![]() .
Тогда
.
Тогда
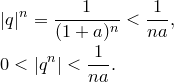
Применим теорему о сжатой последовательности
![]()
Имеем
![]() .
.
Пусть — бесконечно убывающая геометрическая прогрессия. Тогда

Если через
![]() обозначить
сумму членов бесконечно убывающей
геометрической прогрессии, то
обозначить
сумму членов бесконечно убывающей
геометрической прогрессии, то
![]()
Вспомним аксиому непрерывности множества вещественных чисел.
Любое ограниченное
множество
![]() имеет
точную верхнюю границу (т.е. существует
наименьшая из всех верхних границ).
имеет
точную верхнюю границу (т.е. существует
наименьшая из всех верхних границ).
Из определения точной верхней границы множества следует характеристическое свойство точной верхней границы:
Число
![]() называется
точной верхней границей множества
называется
точной верхней границей множества
![]() ,
если
,
если
1) — верхняя граница ;
2)
![]() .
.
Обозначение
![]() .
.
Замечание.
Аналогично определяется точная нижняя
граница множества
—
![]() .
.
Теорема (Вейерштрасс). Любая монотонная ограниченная последовательность имеет предел.
Доказательство.
Докажем теорему для монотонной
возрастающей последовательности
![]() .
Докажем, что точная верхняя граница для
последовательности
.
Докажем, что точная верхняя граница для
последовательности
![]() и
будет ее пределом.
и
будет ее пределом.
Действительно, по определению точной верхней границы
![]()
Кроме того, какое бы
ни взять число
![]() ,
найдется такой номер
,
найдется такой номер
![]() ,
что
,
что
![]()
Так как последовательность
монотонна, то при
![]() будет
будет
![]() ,
а значит, и
,
а значит, и
![]() и
выполняются неравенства
и
выполняются неравенства
![]()
откуда и следует, что
![]() .
.
Приложения.
I. Существование
![]() ,
,
![]()
Пусть
![]() .
Корень
.
Корень
![]() -й
степени из
-й
степени из
![]() —
такое вещественное число
—
такое вещественное число
![]() ,
что
,
что
![]() .
Рассмотрим случай, когда
.
Рассмотрим случай, когда
![]() и
будем искать
и
будем искать
![]() ,
удовлетворяющее этому соотношению,
т.е. арифметическое значение корня.
,
удовлетворяющее этому соотношению,
т.е. арифметическое значение корня.
Возьмем возрастающую
последовательность рациональных чисел
![]() .
.
Докажем, что
последовательность
![]() .
.
Последовательность
![]() возрастает.
Действительно, предположим противное:
возрастает.
Действительно, предположим противное:
![]() .
Тогда, по свойствам неравенств, будем
иметь
.
Тогда, по свойствам неравенств, будем
иметь
![]() ,
что противоречит возрастанию
,
что противоречит возрастанию
![]() .
Аналогично доказывается ее ограниченность.
Возьмем рациональное число
.
Аналогично доказывается ее ограниченность.
Возьмем рациональное число
![]() .
Тогда, очевидно,
.
Тогда, очевидно,
![]() .
Таким образом, последовательность
.
Таким образом, последовательность
![]() имеет
предел. По теореме о пределе произведения
имеет
предел. По теореме о пределе произведения
![]()
т.е.
![]() .
.
II. Число (число Эйлера, число Непера)
Рассмотрим последовательность
![]()
Докажем, что эта последовательность имеет предел. Применим бином Ньютона
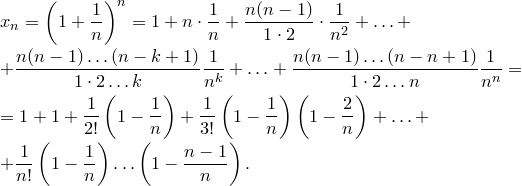
Если от
перейти
к
![]() ,
т.е. увеличить
на
единицу, то, прежде всего, добавится
новый,
,
т.е. увеличить
на
единицу, то, прежде всего, добавится
новый,
![]() -й
полложительный член, каждый же из
написанных
-й
полложительный член, каждый же из
написанных
![]() членов
увеличится, так как любой множитель в
скобках вида
членов
увеличится, так как любой множитель в
скобках вида
![]() заменится
большим множителем
заменится
большим множителем
![]() .
Отсюда и следует, что
.
Отсюда и следует, что
![]() ,
т.е. последовательность
возрастает.
,
т.е. последовательность
возрастает.
Покажем, что она ограничена сверху. Опустив в выражении для все множители в скобках, мы этим увеличим его, так что
![]()
Заменив каждый
множитель в знаменателях дробей числом
![]() ,
мы еще увеличим полученное выражение:
,
мы еще увеличим полученное выражение:
![]()
Но прогрессия,
начинающаяся членом
![]() ,
имеет сумму меньше
,
поэтому
,
имеет сумму меньше
,
поэтому
![]() .
.
19-21) Замечательные пределы
Замечательный тригонометрический предел
![]() (без
доказательства)
(без
доказательства)
Следствия
![]()
![]()
![]()
![]()
Доказательство следствий
![]()
![]()
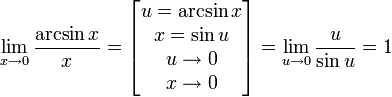
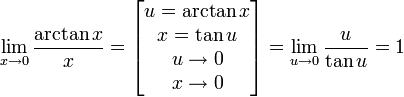
Замечательный показательно-степенной предел
![]() (без
доказательства)
(без
доказательства)
Следствия
![]()
Доказательство следствия
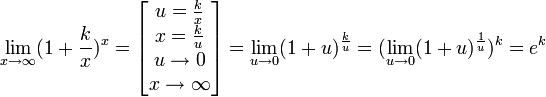
Замечательный логарифмический предел
![]()
Доказательство предела
Используя замечательный
показательно-степенной предел:
![]()
Используя правило
Лопиталя:
![]()
Замечательный показательный предел
![]()
Следствия
![]() для
для
![]() ,
,
![]()
Доказательство предела
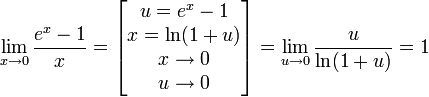
Доказательство следствия
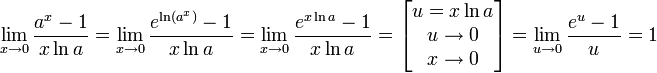
Замечательный степенной предел
|
|
22) Непрерывность функций. Классификация разрывов.
Определение
непрерывности функции в точке.
Функция
f(x)
называется непрерывной
в точке
![]() ,
если предел слева равен пределу справа
и совпадает со значением функции в точке
,
то есть
,
если предел слева равен пределу справа
и совпадает со значением функции в точке
,
то есть
![]() .
Следствие.
ЗНАЧЕНИЕ
ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ
СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ
ТОЧКАХ.
Пример.
Доказать
непрерывность функции
.
Следствие.
ЗНАЧЕНИЕ
ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ
СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ
ТОЧКАХ.
Пример.
Доказать
непрерывность функции
![]() в
точке
в
точке
![]() .
Решение.
Во-первых,
покажем существование предела слева.
Для этого возьмем последовательность
аргументов
.
Решение.
Во-первых,
покажем существование предела слева.
Для этого возьмем последовательность
аргументов
![]() ,
сходящуюся к
,
причем
,
сходящуюся к
,
причем
![]() .
Примером такой последовательности
может являться
.
Примером такой последовательности
может являться
![]() Соответствующая
последовательность значений функции
будет иметь вид
Соответствующая
последовательность значений функции
будет иметь вид
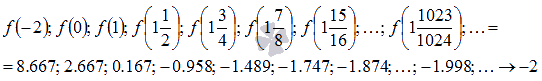 На
рисунке соответствующие значения
показаны зелеными точками.
Легко
видеть, что эта последовательность
сходится к -2,
поэтому
На
рисунке соответствующие значения
показаны зелеными точками.
Легко
видеть, что эта последовательность
сходится к -2,
поэтому
 .
Во-вторых,
покажем существование предела справа.
Для этого возьмем последовательность
аргументов
,
сходящуюся к
,
причем
.
Во-вторых,
покажем существование предела справа.
Для этого возьмем последовательность
аргументов
,
сходящуюся к
,
причем
![]() .
Примером такой последовательности
может являться
.
Примером такой последовательности
может являться
![]() Соответствующая
последовательность значений функции
будет иметь вид
Соответствующая
последовательность значений функции
будет иметь вид
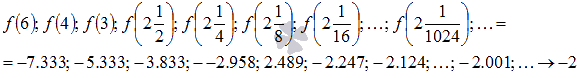 На
рисунке соответствующие значения
показаны синими точками.
Легко
видеть, что эта последовательность
также сходится к -2,
поэтому
На
рисунке соответствующие значения
показаны синими точками.
Легко
видеть, что эта последовательность
также сходится к -2,
поэтому
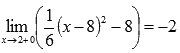 .
Этим
мы показали, что пределы слева и справа
равны, следовательно, существует предел
функции
в
точке
,
причем
.
Этим
мы показали, что пределы слева и справа
равны, следовательно, существует предел
функции
в
точке
,
причем
 Вычислив
значение функции в точке
можно
говорить о выполнении равенства
Вычислив
значение функции в точке
можно
говорить о выполнении равенства
![]() ,
это доказывает непрерывность исходной
функции в точке.
Графическая
иллюстрация.
,
это доказывает непрерывность исходной
функции в точке.
Графическая
иллюстрация.
 Определение
устранимого разрыва первого рода.
В
точке
функция
имеет устранимый
разрыв первого рода,
если предел слева равен пределу справа,
но они не равны значению функции в точке
,то есть
Определение
устранимого разрыва первого рода.
В
точке
функция
имеет устранимый
разрыв первого рода,
если предел слева равен пределу справа,
но они не равны значению функции в точке
,то есть
![]() .
Пример.
Найти
точки разрыва функции и определить их
тип
.
Пример.
Найти
точки разрыва функции и определить их
тип
![]() .
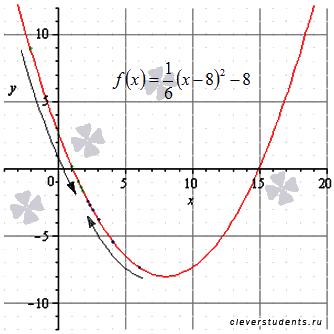
Решение.
Найдем
область
определения функции:
.
Решение.
Найдем
область
определения функции:
 Точкой
разрыва нашей функции может быть только
граничная точка области определения,
то есть
Точкой
разрыва нашей функции может быть только
граничная точка области определения,
то есть
![]() .
Проверим функцию на непрерывность в
этой точке.
На области определения
выражение
.
Проверим функцию на непрерывность в
этой точке.
На области определения
выражение
![]() можно
упростить:
можно
упростить:
![]() Находим
пределы слева и справа. Так как функция
Находим
пределы слева и справа. Так как функция
![]() непрерывна
при любом действительном х,
то
непрерывна
при любом действительном х,
то
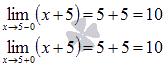 Следовательно,
пределы слева и справа равны, а сама
функция
в
точке
не
определена, поэтому, в точке
функция
имеет устранимый разрыв первого
рода.
Определение
неустранимого разрыва первого рода
(точка скачка функции).
В точке
функция
имеет неустранимый
разрыв первого рода,
если пределы слева и справа НЕ равны,
то есть
Следовательно,
пределы слева и справа равны, а сама
функция
в
точке
не
определена, поэтому, в точке
функция
имеет устранимый разрыв первого
рода.
Определение
неустранимого разрыва первого рода
(точка скачка функции).
В точке
функция
имеет неустранимый
разрыв первого рода,
если пределы слева и справа НЕ равны,
то есть
![]() .
Точку
в
этом случае называют точкой скачка
функции.
Пример.
Исследовать
кусочно-непрерывную функцию
.
Точку
в
этом случае называют точкой скачка
функции.
Пример.
Исследовать
кусочно-непрерывную функцию
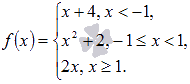 на
непрерывность, определить вид точек
разрыва, сделать чертеж.
Решение.
Разрывы
могут быть лишь в точках
на
непрерывность, определить вид точек
разрыва, сделать чертеж.
Решение.
Разрывы
могут быть лишь в точках
![]() или
или
![]() .
Найдем
пределы слева и справа от этих точек, а
также значения исходной функции в этих
точках.
Слева от точки
наша
функция есть
.
Найдем
пределы слева и справа от этих точек, а
также значения исходной функции в этих
точках.
Слева от точки
наша
функция есть
![]() и
в силу непрерывности линейной функции
и
в силу непрерывности линейной функции
![]() .
В
самой точке
наша
функция есть
.
В
самой точке
наша
функция есть
![]() ,
поэтому
,
поэтому
![]() .
На
промежутке
.
На
промежутке
![]() наша
функция есть
и
в силу непрерывности квадратичной
функции
наша
функция есть
и
в силу непрерывности квадратичной
функции
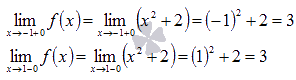 В
точке
наша
функция есть
В
точке
наша
функция есть
![]() ,
поэтому
,
поэтому
![]() .
Справа
от
наша
функция есть
и
в силу непрерывности линейной функции
.
Справа
от
наша
функция есть
и
в силу непрерывности линейной функции
![]() В
итоге имеем:
В
итоге имеем:
![]() следовательно,
в точке
исходная
кусочная функция непрерывна,
следовательно,
в точке
исходная
кусочная функция непрерывна,
![]() ,
то есть
,
то есть
![]() ,
следовательно, в точке
неустранимый
разрыв первого рода (скачок).
Графическая
иллюстрация.
,
следовательно, в точке
неустранимый
разрыв первого рода (скачок).
Графическая
иллюстрация.
 Определение
разрыва второго рода (бесконечный
разрыв).
В точке
функция
имеет разрыв
второго рода,
если либо предел слева
Определение
разрыва второго рода (бесконечный
разрыв).
В точке
функция
имеет разрыв
второго рода,
если либо предел слева
![]() ,
либо предел справа
,
либо предел справа
![]() ,
не существует или бесконечен.
Пример.
Исследовать
функцию
,
не существует или бесконечен.
Пример.
Исследовать
функцию
![]() на
непрерывность, определить вид точек
разрыва, сделать чертеж.
Решение.
Областю
определения функции является интервал
на
непрерывность, определить вид точек
разрыва, сделать чертеж.
Решение.
Областю
определения функции является интервал
![]() .
Найдем
пределы функции слева и справа от точки
.
Найдем
пределы функции слева и справа от точки
![]() .
Рассмотрим
произвольную последовательность
значений аргумента, сходящуюся к
слева.
Например,
.
Рассмотрим
произвольную последовательность
значений аргумента, сходящуюся к
слева.
Например,
![]() и
соответствующую ей последовательность
значений функции
и
соответствующую ей последовательность
значений функции
 Легко
показать, что эта последовательность
бесконечно большая отрицательная,
поэтому,
Легко
показать, что эта последовательность
бесконечно большая отрицательная,
поэтому,
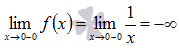 .
Рассмотрим
произвольную последовательность
значений аргумента, сходящуюся к
справа.
Например,
.
Рассмотрим
произвольную последовательность
значений аргумента, сходящуюся к
справа.
Например,
![]() и
соответствующую ей последовательность
значений функции
и
соответствующую ей последовательность
значений функции
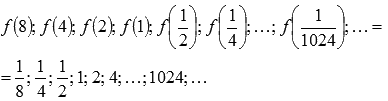 Легко
показать, что эта последовательность
бесконечно большая положительная,
поэтому,
Легко
показать, что эта последовательность
бесконечно большая положительная,
поэтому,
![]() .
Следовательно,
в точке
функция
имеет разрыв второго рода.
Графическая
иллюстрация:
23)
Производная. Основные свойства.
.
Следовательно,
в точке
функция
имеет разрыв второго рода.
Графическая
иллюстрация:
23)
Производная. Основные свойства.

П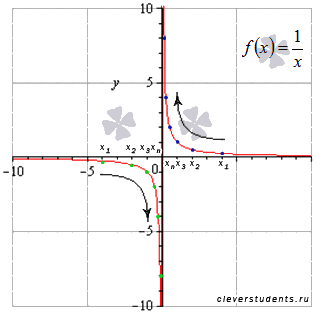 роизводная
-
основное понятие дифференциального
исчисления, характеризующее скорость
изменения функции (в данной точке).
Определяется как предел отношения
приращения функции к приращению ее
аргумента при стремлении приращения
аргумента к нулю, если такой предел
существует. Функцию, имеющую конечную
производную (в некоторой точке), называют
дифференцируемой (в данной точке).
Процесс вычисления производной называется
дифференци́рованием. Обратный процесс
— интегрирование.
роизводная
-
основное понятие дифференциального
исчисления, характеризующее скорость
изменения функции (в данной точке).
Определяется как предел отношения
приращения функции к приращению ее
аргумента при стремлении приращения
аргумента к нулю, если такой предел
существует. Функцию, имеющую конечную
производную (в некоторой точке), называют
дифференцируемой (в данной точке).
Процесс вычисления производной называется
дифференци́рованием. Обратный процесс
— интегрирование.
25) Таблица производных элементарных функций с доказательством.

Вывод
производной константы.
При выводе
самой первой формулы таблицы будем
исходить из определения
производной
функции в точке. Возьмем
![]() ,
где x
– любое действительное число, то есть,
x
– любое число из области определения
функции
,
где x
– любое действительное число, то есть,
x
– любое число из области определения
функции
![]() .
Запишем предел отношения приращения
функции к приращению аргумента при
.
Запишем предел отношения приращения
функции к приращению аргумента при
![]() :
:
![]() Следует
заметить, что под знаком предела
получается выражение
Следует
заметить, что под знаком предела
получается выражение
![]() ,
которое не является неопределенностью
ноль делить на ноль,
так как в числителе находится не
бесконечно малая величина, а именно
ноль. Другими словами, приращение
постоянной функции всегда равно
нулю.
Таким образом, производная
постоянной функции
равна
нулю на всей области определения.
,
которое не является неопределенностью
ноль делить на ноль,
так как в числителе находится не
бесконечно малая величина, а именно
ноль. Другими словами, приращение
постоянной функции всегда равно
нулю.
Таким образом, производная
постоянной функции
равна
нулю на всей области определения.
Вывод
производной степенной функции.
Формула
производной степенной функции имеет
вид
![]() ,
где показатель степени p
– любое действительное число.
Докажем
сначала формулу для натурального
показателя степени, то есть, для p
= 1, 2, 3, …
Будем
пользоваться определением производной.
Запишем предел отношения приращения
степенной функции к приращению
аргумента:
,
где показатель степени p
– любое действительное число.
Докажем
сначала формулу для натурального
показателя степени, то есть, для p
= 1, 2, 3, …
Будем
пользоваться определением производной.
Запишем предел отношения приращения
степенной функции к приращению
аргумента:
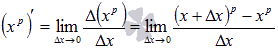 Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
 Следовательно,
Следовательно,
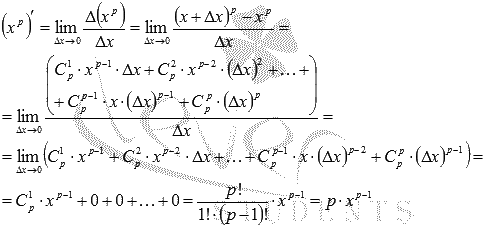 Этим
доказана формула производной степенной
функции для натурального показателя.
При
доказательстве формулы для любого
действительного p
воспользуемся логарифмической
производной
(не путайте с производной логарифмической
функции). Для понимания процесса,
рекомендуем сначала ознакомиться с
производной
логарифмической функции,
а также разобраться с разделами теории
производная
неявно заданной функции
и производная
сложной функции.
Следует
рассмотреть два случая: при положительных
x
и отрицательных x.
Сначала
будем полагать
Этим
доказана формула производной степенной
функции для натурального показателя.
При
доказательстве формулы для любого
действительного p
воспользуемся логарифмической
производной
(не путайте с производной логарифмической
функции). Для понимания процесса,
рекомендуем сначала ознакомиться с
производной
логарифмической функции,
а также разобраться с разделами теории
производная
неявно заданной функции
и производная
сложной функции.
Следует
рассмотреть два случая: при положительных
x
и отрицательных x.
Сначала
будем полагать
![]() .
В этом случае
.
В этом случае
![]() .
Выполним логарифмирование равенства
.
Выполним логарифмирование равенства
![]() по
основанию e
и применим свойство логарифма:
по
основанию e
и применим свойство логарифма:
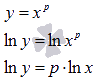 Пришли
к неявно заданной функции. Находим ее
производную:
Пришли
к неявно заданной функции. Находим ее
производную:
 Осталось
провести доказательство для отрицательных
x.
Когда
показатель p
представляет собой четное число или
рациональную дробь с нечетным знаменателем
и четным числителем, то степенная функция
определена и при
Осталось
провести доказательство для отрицательных
x.
Когда
показатель p
представляет собой четное число или
рациональную дробь с нечетным знаменателем
и четным числителем, то степенная функция
определена и при
![]() ,
причем является четной). То есть,
,
причем является четной). То есть,
![]() .
В этом случае
и
также можно использовать доказательство
через логарифмическую производную.
Когда показатель p
представляет собой нечетное число или
рациональную дробь с нечетным знаменателем
и нечетным числителем, то степенная
функция определена и при
,
причем является нечетной. То есть,
.
В этом случае
и
также можно использовать доказательство
через логарифмическую производную.
Когда показатель p
представляет собой нечетное число или
рациональную дробь с нечетным знаменателем
и нечетным числителем, то степенная
функция определена и при
,
причем является нечетной. То есть,
![]() .
В этом случае
.
В этом случае
![]() и
логарифмическую производную использовать
нельзя. Для доказательства формулы
в
этом случае можно воспользоваться
правилами
дифференцирования
и правилом нахождения производной
сложной функции:
и
логарифмическую производную использовать
нельзя. Для доказательства формулы
в
этом случае можно воспользоваться
правилами
дифференцирования
и правилом нахождения производной
сложной функции:
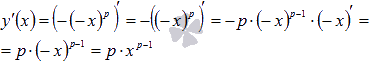 Последний
переход возможен в силу того, что если
p
- нечетное число или рациональную дробь
с нечетным знаменателем и нечетным
числителем, то p-1
либо четное число, либо рациональная
дробь с нечетным знаменателем и четным
числителем, поэтому
Последний
переход возможен в силу того, что если
p
- нечетное число или рациональную дробь
с нечетным знаменателем и нечетным
числителем, то p-1
либо четное число, либо рациональная
дробь с нечетным знаменателем и четным
числителем, поэтому
![]() .
Таким
образом, формула производной степенной
функции доказана для любого действительного
p.
.
Таким
образом, формула производной степенной
функции доказана для любого действительного
p.
Вывод
производной показательной функции
Вывод
формулы производной приведем на основе
определения:
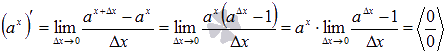 Пришли
к неопределенности. Для ее раскрытия
введем новую переменную
Пришли
к неопределенности. Для ее раскрытия
введем новую переменную
![]() ,
причем
,
причем
![]() при
.
Тогда
при
.
Тогда
![]() .
В последнем переходе мы использовали
формулу перехода к новому основанию
логарифма.
Выполним подстановку
в исходный предел:
.
В последнем переходе мы использовали
формулу перехода к новому основанию
логарифма.
Выполним подстановку
в исходный предел:
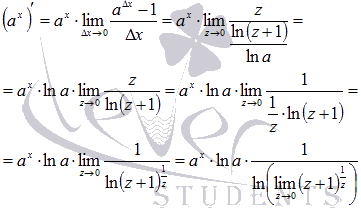 Если
вспомнить второй
замечательный предел,
то придем к формуле производной
показательной функции:
Если
вспомнить второй
замечательный предел,
то придем к формуле производной
показательной функции:
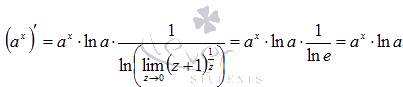
Вывод производной логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x
из области определения и всех допустимых
значениях основания a
логарифма. По определению производной
имеем:
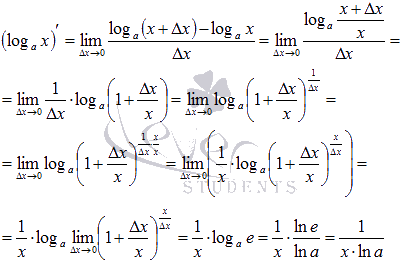 Как
Вы заметили, при доказательстве
преобразования проводились с использованием
свойств логарифма. Равенство
Как
Вы заметили, при доказательстве
преобразования проводились с использованием
свойств логарифма. Равенство
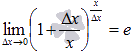 справедливо
в силу второго замечательного предела.
справедливо
в силу второго замечательного предела.
Производные
тригонометрических функций.
Для
вывода формул производных тригонометрических
функций нам придется вспомнить некоторые
формулы тригонометрии, а также первый
замечательный предел.
По
определению производной для функции
синуса имеем
![]() .
Воспользуемся
формулой разности синусов:
.
Воспользуемся
формулой разности синусов:
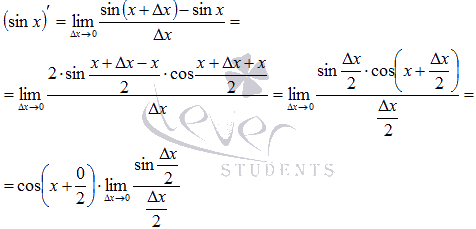 Осталось
обратиться к первому замечательному
пределу:
Осталось
обратиться к первому замечательному
пределу:
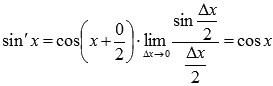 Таким
образом, производная функции sin
x есть cos
x.
Абсолютно
аналогично доказывается формула
производной косинуса.
Таким
образом, производная функции sin
x есть cos
x.
Абсолютно
аналогично доказывается формула
производной косинуса.
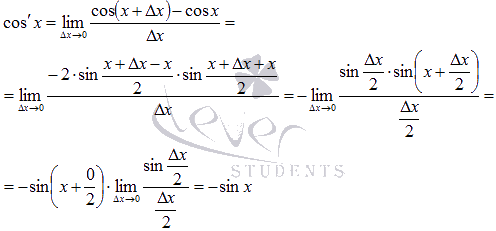 Следовательно,
производная функции cos
x есть –sin
x.
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Следовательно,
производная функции cos
x есть –sin
x.
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
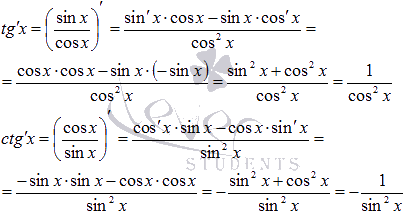
26) Производная обратных функций. Вывод формул производных обратных тригонометрических функций.
,
![]() -
это производная функции f(x)
по x.
Теперь
сформулируем правило
нахождения производной обратной
функции.
Пусть
функции y =
f(x) и x
= g(y) взаимно
обратные, определенные на интервалах
-
это производная функции f(x)
по x.
Теперь
сформулируем правило
нахождения производной обратной
функции.
Пусть
функции y =
f(x) и x
= g(y) взаимно
обратные, определенные на интервалах
![]() и
и
![]() соответственно.
Если в точке
соответственно.
Если в точке
![]() существует
конечная отличная от нуля производная
функции f(x),
то в точке
существует
конечная отличная от нуля производная
функции f(x),
то в точке
![]() существует
конечная производная обратной функции
g(y),
причем
существует
конечная производная обратной функции
g(y),
причем
![]() .
В другой записи
.
В другой записи
![]() .
Можно
это правило переформулировать для
любого x
из промежутка
.
Можно
это правило переформулировать для
любого x
из промежутка
![]() ,
тогда получим
,
тогда получим
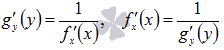 .
Давайте
проверим справедливость этих
формул.
Найдем обратную функцию
для натурального логарифма
.
Давайте
проверим справедливость этих
формул.
Найдем обратную функцию
для натурального логарифма
![]() (здесь
y
– функция, а x
- аргумент). Разрешив это уравнение
относительно x,
получим
(здесь
y
– функция, а x
- аргумент). Разрешив это уравнение
относительно x,
получим
![]() (здесь
x
– функция, а y
– ее аргумент). То есть,
и
взаимно
обратные функции.
Из таблицы
производных
видим, что
(здесь
x
– функция, а y
– ее аргумент). То есть,
и
взаимно
обратные функции.
Из таблицы
производных
видим, что
![]() и
и
![]() .
Убедимся,
что формулы нахождения производных
обратной функции приводят нас к этим
же результатам:
.
Убедимся,
что формулы нахождения производных
обратной функции приводят нас к этим
же результатам:
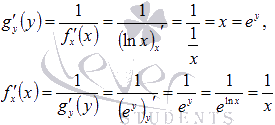 Как
видите, получили такие же результаты
как и в таблице производных.
Теперь
мы обладаем знаниями для доказательства
формул производных обратных
тригонометрических функций.
Начнем
с производной арксинуса.
Для
Как
видите, получили такие же результаты
как и в таблице производных.
Теперь
мы обладаем знаниями для доказательства
формул производных обратных
тригонометрических функций.
Начнем
с производной арксинуса.
Для
![]() обратной
функцией является
обратной
функцией является
![]() .
Тогда по формуле производной обратной
функции получаем
.
Тогда по формуле производной обратной
функции получаем
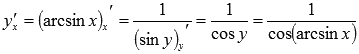 Осталось
провести преобразования.
Так как
областью значений арксинуса является
интервал
Осталось
провести преобразования.
Так как
областью значений арксинуса является
интервал
![]() ,
то
,
то
![]() (смотрите
раздел основные
элементарные функции, их свойства и
графики).
Поэтому
(смотрите
раздел основные
элементарные функции, их свойства и
графики).
Поэтому
![]() ,
а
,
а
![]() не
рассматриваем.
Следовательно,
не
рассматриваем.
Следовательно,
![]() .
Областью определения производной
арксинуса является промежуток (-1;
1).
Для
арккосинуса все делается абсолютно
аналогично:
.
Областью определения производной
арксинуса является промежуток (-1;
1).
Для
арккосинуса все делается абсолютно
аналогично:
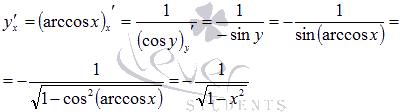 Найдем
производную арктангенса.
Для
Найдем
производную арктангенса.
Для
![]() обратной
функцией является
обратной
функцией является
 .
.
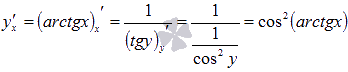 Выразим
арктангенс через арккосинус, чтобы
упростить полученное выражение.
Пусть
arctgx = z,
тогда
Выразим
арктангенс через арккосинус, чтобы
упростить полученное выражение.
Пусть
arctgx = z,
тогда
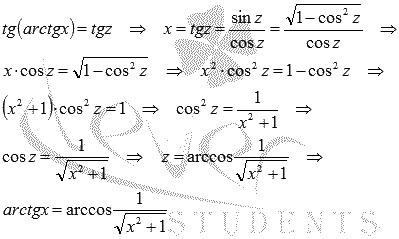 Следовательно,
Следовательно,
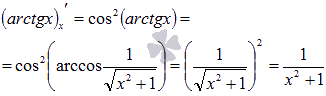 Схожим
образом находится производная
арккотангенса:
Схожим
образом находится производная
арккотангенса:
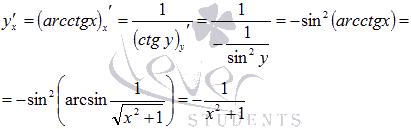
27) Производная неявной функции. Пример.
функция
подразумевает соответствие между
множеством значений величины x
и множеством значений y,
причем это соответствие НЕ обязательно
устанавливается какой-либо формулой
или аналитическим выражением. То есть,
существует множество способов задания
функции помимо привычного
![]() .
В
данной статье мы рассмотрим неявные
функции и способы нахождения их
производных.
В качестве примеров функций, заданных
неявно, можно привести
.
В
данной статье мы рассмотрим неявные
функции и способы нахождения их
производных.
В качестве примеров функций, заданных
неявно, можно привести
![]() или
или
![]() .
Как
Вы заметили, неявная функция определяется
соотношением
.
Как
Вы заметили, неявная функция определяется
соотношением
![]() .
Но не все такие соотношения между x
и y
задают функцию. Например, ни одна пара
действительных чисел x
и y
не удовлетворяет равенству
.
Но не все такие соотношения между x
и y
задают функцию. Например, ни одна пара
действительных чисел x
и y
не удовлетворяет равенству
![]() ,
следовательно, это соотношение неявную
функцию не задает.
может
неявно определять закон соответствия
между величинами x
и y,
причем каждому значению аргумента x
может соответствовать как одно (в этом
случае имеем однозначную функцию) так
и несколько значений функции (в этом
случае функцию называют многозначной).
К примеру, значению x
= 1 соответствует
два действительных значения y
= 2 и y
= -2 неявно
заданной функции
.
Неявную
функцию
привести
к явному виду далеко не всегда возможно,
иначе не пришлось бы дифференцировать
сами неявные функции. Например,
,
следовательно, это соотношение неявную
функцию не задает.
может
неявно определять закон соответствия
между величинами x
и y,
причем каждому значению аргумента x
может соответствовать как одно (в этом
случае имеем однозначную функцию) так
и несколько значений функции (в этом
случае функцию называют многозначной).
К примеру, значению x
= 1 соответствует
два действительных значения y
= 2 и y
= -2 неявно
заданной функции
.
Неявную
функцию
привести
к явному виду далеко не всегда возможно,
иначе не пришлось бы дифференцировать
сами неявные функции. Например,
![]() -
не преобразовывается к явному виду, а
-
не преобразовывается к явному виду, а
![]() -
преобразовывается.
Теперь к
делу.
Чтобы найти производную
неявно заданной функции, необходимо
продифференцировать обе части равенства
по
аргументу x,
считая y
– функцией от x,
и после этого выразить
-
преобразовывается.
Теперь к
делу.
Чтобы найти производную
неявно заданной функции, необходимо
продифференцировать обе части равенства
по
аргументу x,
считая y
– функцией от x,
и после этого выразить
![]() .
.
28) Вычисление производных сложных функций. Пример.
Сложная
функция –
это функция, аргументом которой также
является функция.
С нашей точки
зрения, это определение наиболее понятно.
Условно можно обозначать как f(g(x)).
То есть, g(x)
как бы аргумент функции f(g(x)).
К
примеру, пусть f
– функция арктангенса, а g(x)
= lnx есть
функция натурального логарифма, тогда
сложная функция f(g(x))
представляет собой arctg(lnx).
Еще пример: f
– функция возведения в четвертую
степень, а
![]() -
целая рациональная функция (смотрите
классификацию
элементарных функций),
тогда
-
целая рациональная функция (смотрите
классификацию
элементарных функций),
тогда
![]() .
В
свою очередь, g(x)
также может быть сложной функцией.
Например,
.
В
свою очередь, g(x)
также может быть сложной функцией.
Например,
 .
Условно такое выражение можно обозначить
как
.
Условно такое выражение можно обозначить
как
![]() .
Здесь f
– функция синуса,
.
Здесь f
– функция синуса,
![]() -
функция извлечения квадратного корня,
-
функция извлечения квадратного корня,
![]() -
дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом
-
дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом
![]() .
Часто
можно слышать, что сложную функцию
называют композицией
функций.
Формула
нахождения производной сложной
функции.
.
Часто
можно слышать, что сложную функцию
называют композицией
функций.
Формула
нахождения производной сложной
функции.
![]() Пример.
Найти
производную сложной функции
Пример.
Найти
производную сложной функции
![]() .
Решение.
В
данном примере f
– функция возведения в квадрат, а g(x)
= 2x+1 – линейная
функция.
Вот подробное решение с
использованием формулы производной
сложной функции:
.
Решение.
В
данном примере f
– функция возведения в квадрат, а g(x)
= 2x+1 – линейная
функция.
Вот подробное решение с
использованием формулы производной
сложной функции:
 Давайте
найдем эту производную, предварительно
упростив вид исходной
функции.
Давайте
найдем эту производную, предварительно
упростив вид исходной
функции.
![]() Следовательно,
Следовательно,
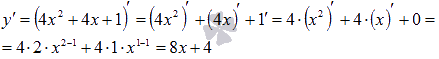
29) Дифференциал и его геометрический смысл
Пусть
функция ![]() определена
на промежутке
определена
на промежутке ![]() и
дифференцируема в окрестности
точки
и
дифференцируема в окрестности
точки ![]() ,тогда
,тогда ![]() или
по теореме о связи бесконечно малых с
пределами функций имеем
или
по теореме о связи бесконечно малых с
пределами функций имеем ![]() ,
где
,
где ![]() -
бесконечно малая величина при
-
бесконечно малая величина при ![]() .
Отсюда:
.
Отсюда:
![]() . (
7.1)
. (
7.1)
Таким
образом, приращение функции ![]() состоит
из двух слагаемых:
состоит
из двух слагаемых:
1) ![]() -
линейного относительно
-
линейного относительно ![]() ,
т.к.
,
т.к. ![]() ;
;
2) ![]() -
нелинейного относительно
,
т.к.
-
нелинейного относительно
,
т.к. ![]() .Определение. Дифференциалом
функции называется главная, линейная
относительно
часть
приращения функции, равная произведению
производной на приращение независимой
переменной:
.Определение. Дифференциалом
функции называется главная, линейная
относительно
часть
приращения функции, равная произведению
производной на приращение независимой
переменной:![]() . (
7.2)
. (
7.2)
|
Геометрический
смысл. На
графике функции |
Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда получает приращение .
30) Монотонность функции и определение экстремума по первой производной
Оказывается, монотонность функции связана с тем, каков знак ее производной:
Если производная положительна, то функция возрастает
Если производная отрицательна, то функция убывает
Это помогает исследовать монотонность: теперь вместо неравенства с двумя неизвестными х1 и х2 можно рассматривать неравенство с одной неизвестной x. К тому же часто бывает так, что производная функции сама по себе проще исходной функции.
Функция |
Производная |
Монотонность |
Линейная
|
|
Если
|
Если
|
||
Если
|
||
Прямая
пропорциональность
|
|
Если
|
Если
|
||
Обратная
пропорциональность
|
|
Если
,
убывает
на
|
Если , возрастает на и на |
||
Квадратичная
функция
|
|
Если
,
убывает на
|
Если , возрастает на , убывает на |
||
|
|
Возрастает
на
|
Определение экстремума: приравнивание производной к нулю.
31) Выпуклость функций и связь со второй производной. Точки перегиба.
Связь выпуклости (вогнутости) функции с поведением ее производной
Определение 1. Функция f(x)
называется выпуклой на отрезке [a,
b], если
![]()
![]() выполнено условие
выполнено условие
![]() .
.
Примерный вид графика выпуклой функции приведен на рис. 3.7. Его отличительной особенностью является то, что график выпуклой функции лежит под хордой, соединяющей две любые ее точки.
Определение 2. Функция f(x) называется вогнутой на отрезке [a, b], если выполнено условие
![]() .
.
Теорема. Пусть f(x)
определена и непрерывна на [a,
b] и
![]() имеет конечную производную. Для того,
чтобы f(x)
была выпуклой (вогнутой) необходимо и
достаточно, чтобы
имеет конечную производную. Для того,
чтобы f(x)
была выпуклой (вогнутой) необходимо и
достаточно, чтобы
![]() монотонно возрастала (убывала).
монотонно возрастала (убывала).
Следствие. Пусть f(x)
и
непрерывны на [a, b]
и
существует
![]() .
Тогда для того, чтобы f(x)
была выпуклой (вогнутой) необходимо и
достаточно, чтобы
.
Тогда для того, чтобы f(x)
была выпуклой (вогнутой) необходимо и
достаточно, чтобы
![]() (
(![]() ).
).
|
32) Первообразная и неопределенный интеграл. Основные свойства.
Определение
первообразной.
Первообразной
функции f(x)
на промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство
![]() для
любого х
из заданного промежутка.
Если
принять во внимание тот факт, что
производная от константы С
равна нулю, то справедливо равенство
для
любого х
из заданного промежутка.
Если
принять во внимание тот факт, что
производная от константы С
равна нулю, то справедливо равенство
![]() .
Таким образом, функция f(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.
Все
множество первообразных функции f(x)
называется неопределенным интегралом
этой функции и обозначается
.
Таким образом, функция f(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.
Все
множество первообразных функции f(x)
называется неопределенным интегралом
этой функции и обозначается
![]() .
Выражение
.
Выражение
![]() называют
подынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие
нахождения неизвестной функции по
заданному ее дифференциалу называется
неопределенным
интегрированием, потому что результатом
интегрирования является не одна функция
F(x),
а множество ее первообразных F(x)+C.
На
основании свойств производной можно
сформулировать и доказать свойства
неопределенного интеграла
(свойства первообразной).
называют
подынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие
нахождения неизвестной функции по
заданному ее дифференциалу называется
неопределенным
интегрированием, потому что результатом
интегрирования является не одна функция
F(x),
а множество ее первообразных F(x)+C.
На
основании свойств производной можно
сформулировать и доказать свойства
неопределенного интеграла
(свойства первообразной).
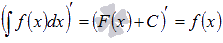 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции.
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
 ,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
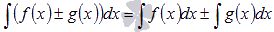 Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
33) Основные формулы вычисления интегралов.
34) Табличные интегралы с корнями
35) Интегрирование по частям и заменой переменной
![]()
![]() Пример:
Пример:
![]()
36) Определенный интеграл. Геометрическая интерпретация. Формула Ньютона-Лейбница.
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:
где
Свойства определенного интеграла Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b].
Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на [a, b], то
Площадь криволинейной трапеции Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и графиком функции f (x) (рисунок 1), определяется по формуле
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой
Замена переменной в определенном интеграле Определенный
интеграл
Новые пределы интегрирования по переменной t определяются выражениями
где g -1 - обратная функция к g, т.е. t = g -1(x). Интегрирование по частям для определенного интеграла В этом случае формула интегрирования по частям имеет вид:
где
|
|
37) Несобственный интеграл и его сходимость
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Предел a или b (или оба предела) являются бесконечными;
Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
38) Интеграл Эйлера-Пуассона
Га́уссов интегра́л (также интеграл Э́йлера — Пуассо́на или интеграл Пуассона[1]) — интеграл от гауссовой функции:
![]()
Гауссовы интегралы от масштабированной гауссовой функции
![]()
и многомерные гауссовы интегралы
![]()
элементарно сводятся к обычному одномерному, описанному первым (здесь и ниже везде подразумевается интегрирование по всему пространству).
То же относится к многомерным интегралам вида
где x — вектор, а M — симметричная матрица с отрицательными собственными числами, так как такие интегралы сводятся к предыдущему, если сделать преобразование координат, диагонализующее матрицу М.
39) Числовые ряды, сходимость, сумма бесконечно убывающей геометрической прогрессии.
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
вещественные числовые ряды — изучаются в математическом анализе;
комплексные числовые ряды — изучаются в комплексном анализе;
числовой ряд сходится, если сходится последовательность его частичных сумм;
числовой ряд расходится, если расходится последовательность его частичных сумм:
числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.
Необходимый признак сходимости, вообще говоря, не гарантирует сходимости ряда. Сходимость или расходимость ряда устанавливается с помощью достаточных признаков. Признаки сравнения, которые мы рассмотрим ниже, как раз и представляют собой достаточные признаки сходимости или расходимости рядов. Признаки сравнения рядов Даны
два ряда
Если сходится, то также сходится; Если расходится, то также расходится. Предельные признаки сравнения рядов Пусть даны два ряда и , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки:
Так называемый
обобщенный
гармонический ряд
|
|
По определению суммой бесконечного числа слагаемых a1, a2, ..., an, ... называется предел суммы Sn первых п чисел, когда п—> ∞:
S
=![]() Sn =
(a1
+ a2 + ... + an).
(2)
Sn =
(a1
+ a2 + ... + an).
(2)
Предел (2), конечно, может существовать, а может и не существовать. Соответственно этому говорят, что сумма (1) существует или не существует.
Как же выяснить, существует ли сумма (1) в каждом конкретном случае? Общее решение этого вопроса выходит далеко за пределы нашей программы. Однако существует один важный частный случай, который нам предстоит сейчас рассмотреть. Речь будет идти о суммировании членов бесконечно убывающей геометрической прогрессии.
Пусть a1 , a1q , a1q2, ...— бесконечно убывающая геометрическая прогрессия. Это означает, что | q |< 1. Сумма первых п членов этой прогрессии равна
![]()
Из основных теорем о пределах переменных величин (см. § 136) получаем:

Но 1 = 1, a qn = 0. Поэтому
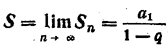
Итак, сумма бесконечно убывающей геометрической прогрессии равна первому члену этой прогрести, деленному на единицу минус знаменатель этой прогрессии.

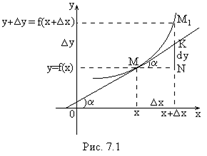

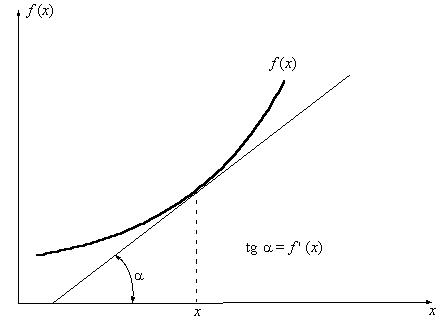
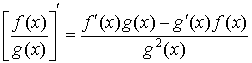 ;
;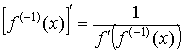 .
.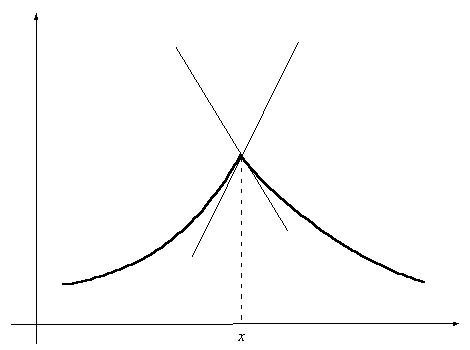

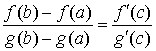 .
.
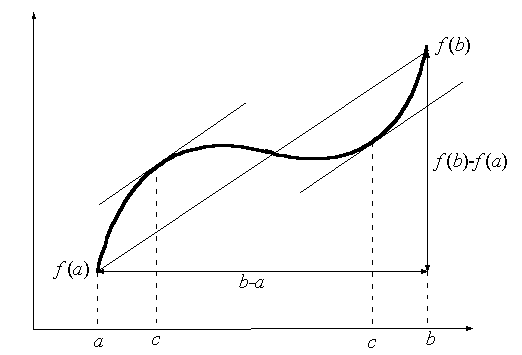
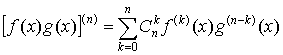 .
.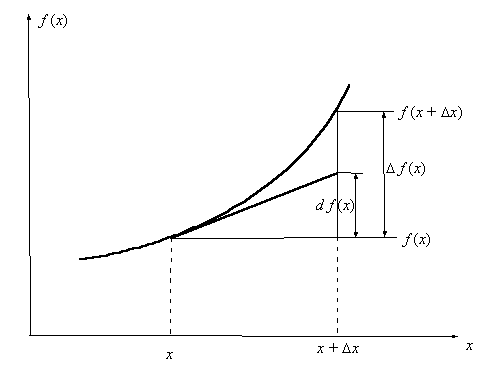
 ;
;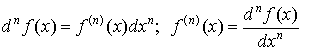 .
. ).
).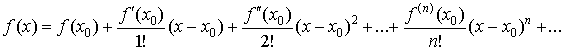
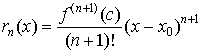 ,
,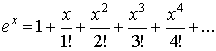 ;
;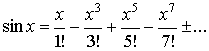 ;
;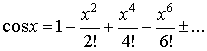 ;
;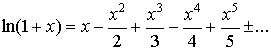
 ,
,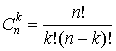 .
.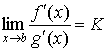 .
. .
.


 .
. .
.
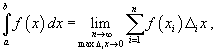
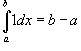
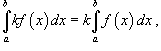 где
k
- константа;
где
k
- константа;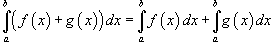
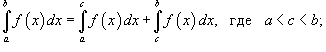
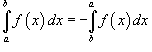
 по
переменной x
можно преобразовать в определенный
интеграл относительно переменной t
с помощью подстановки x
= g (t):
по
переменной x
можно преобразовать в определенный
интеграл относительно переменной t
с помощью подстановки x
= g (t):
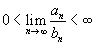 ,
то оба ряда
и
либо
сходятся, либо расходятся;
,
то оба ряда
и
либо
сходятся, либо расходятся;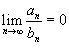 ,
то ряд
сходится,
если сходится ряд
;
,
то ряд
сходится,
если сходится ряд
;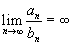 ,
то ряд
расходится,
если расходится ряд
.
,
то ряд
расходится,
если расходится ряд
.