95.Парна лінійна регресія. ,їх властивості та зв'язок між ними.

Коефіцієнт детермінації,та коеф.кореляції-це кількісні характеристики дисперсійного аналізу,за якими можна зробити висновок- наскільки побудована економт.модель узгоджується з емпіричною інформацією, на підставі якої її побудовано, тобто чи достовірна економ.модель.

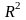показує на скільки % варіація залежної змінної визначається варіацією незалежних змінних.

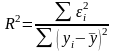
Коефіц.кореляції характеризує тісноту(щільність) зв'язку між залежними та пояснювальними змінними: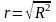

Якщо X та Y — незалежні, то коефіцієнт кореляції дорівнює 0. Зворотнє твердження невірне. Коефіцієнт кореляції може дорівнювати 0 навіть якщо Y є функцією від X

Значення належать множині [0;1].Чим ближче до 1,тим більшою є адекватність побудованої моделі данних спостер.

Відповідно, чим ближче r до 1,тим щільніший зв'язок. коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції. Тому коефіцієнт кореляції може розраховуватись за формулою

96.Парна лінійна регресія. Визнач.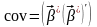 Парна лінійна регресія є лінійною фінкцією між залежною змінною У і однією пояснюючою змінною Х.

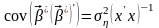де,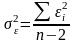

97.Парна лінійна регерсія. Визначення виправленої дисперсії

Виправлена дисперсія є точковою незміщенною статистичною оцінкою для

і визначається за формулою: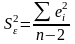 де,

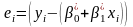
98.Парна лінійна регресія. Визначення емпіричного вектора для цієї регресії, використовуючи метод найменших квадратів( мнк)

МНК полягає в знаходженні таких оцінок параметрів

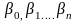
з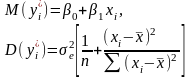 а яких сума квадратів відхилень спостережуваних значень показника від розрахункових буде найменша.

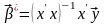де,

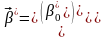
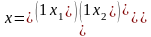
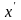-матриця транспонована до матриці Х. Матриця крім вектора незалежних змінних містить вектор одиниць.Він дописується в матриці ліворуч тоді, коли економетрична модель має вільний член.

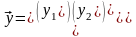
99.Парна лінійна регресія. Визначення коефіцієнта детермінації для цієї регресії .

Парна лінійна регресія є лінійною фінкцією між залежною змінною У і однією пояснюючою змінною Х.

Частка дисперсії,що пояснює регресію називається коеф.детермінації .

Він використовується як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної змінної Х та показує, на скільки % варіація залежної змінної визначається варіацією пояснюючих змінних. І визначається за формулою:

Чим ближче до 1,тим більшою є адекватність побудованої моделі данних спостережень.

100.Парна лінійна регресія. Довести, що

Парна лінійна регресія вивчає звязок між двома ознаками та має наступний вигляд:

.

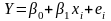Таким чином:

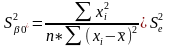
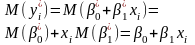
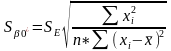
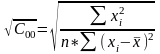Тому:

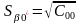
Аналогічно:

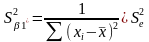
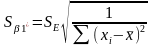
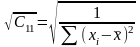
Т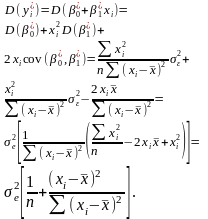 ому: 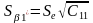Парна

101.Парна лінійна регресія. Емпірична парна лінійна регресія та її числові характеристики 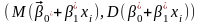Парна лінійна регресія вивчає звязок між двома ознаками та має наступний вигляд:

.

Емпірична парна лінійна регресія має вигляд (модель):

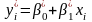
Отримане за моделлю значення залежної змінної є випадковою величиною, бо визначається випадковими емпіричними коефіцієнтами .

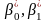Враховуючи це, можемо визначити для 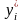основні числові характеристики, а саме

Таким чином маємо: