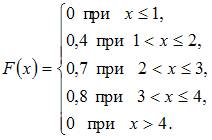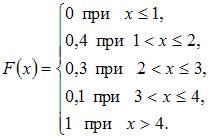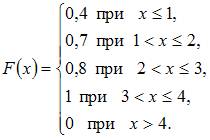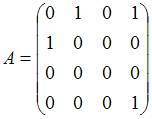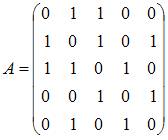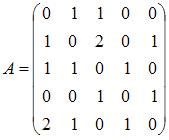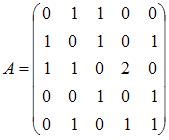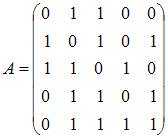3)Тема: Особые точки функции комплексного переменного:
Число
особых точек функции 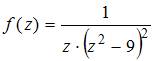 равно
… 3
равно
… 3
4)Тема: Операции над комплексными числами
Произведение
комплексных чисел 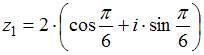 и
и 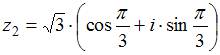 равно
равно ![]()
Решение:
Произведение двух комплексных чисел,
заданных в тригонометрической
форме,
находится по формуле: ![]() В
нашем случае получим
В
нашем случае получим 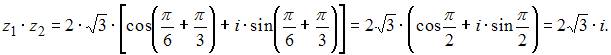
Тема: Дифференцирование функции комплексного переменного Если , то равно 4.
Решение: Производная функции равна тогда
Тема:
Особые точки функции комплексного
переменного
Для
функции 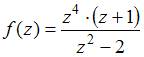 точка
является
точка
является
полюсом третьего порядка
Решение:
Порядок
полюса функции вида
равен
порядку нуля
.
Т.к.  то
точка
является
полюсом третьего порядка.
то
точка
является
полюсом третьего порядка.
Тема:
Операции над комплексными числами
Сумма
комплексных чисел
и
равна ![]()
Тема:
Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству![]() ,
изображенному на рисунке:
,
изображенному на рисунке:
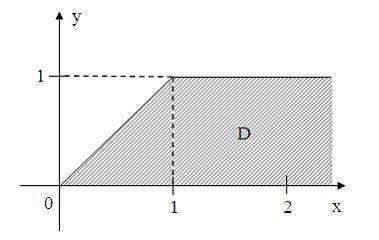
удовлетворяют
условию …![]()
Решение:
Множество
,
изображенное на рисунке, ограничено
прямыми ![]() Для
комплексного числа
:
Для
комплексного числа
:![]() –
действительная часть
–
действительная часть ![]() ,
, ![]() -
мнимая часть, угол наклона прямой
-
мнимая часть, угол наклона прямой ![]() к
оси х равен
.
Следовательно, комплексные числа
должны
удовлетворять условиям
к
оси х равен
.
Следовательно, комплексные числа
должны
удовлетворять условиям![]() .
.
Тема:
Операции над комплексными
числами
Частное ![]() комплексных
чисел
комплексных
чисел ![]() и
и ![]() равно
…
равно
…![]()
Решение:
Частное
двух комплексных чисел находится по
формуле 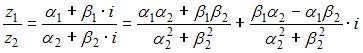 .
В
нашем случае получим
.
В
нашем случае получим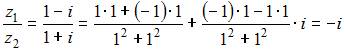
Тема:
Особые точки функции комплексного
переменного
Для
функции 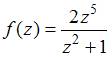 точка
является
…
точка
является
…
|
|
|
полюсом третьего порядка |
Решение:
Порядок
полюса функции вида
равен
порядку нуля
.
Так
как 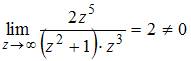 ,
то точка
будет
полюсом третьего порядка.
,
то точка
будет
полюсом третьего порядка.
Тема: Области на комплексной плоскости Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке:
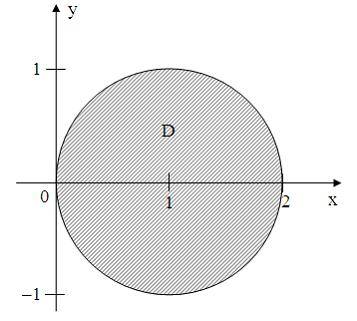
удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Множество
,
изображенное на рисунке, представляет
собой круг с центром в точке ![]() и
радиусом
и
радиусом ![]() .
Уравнение окружности радиуса
с
центром в точке
.
Уравнение окружности радиуса
с
центром в точке ![]() имеет
вид:
.
Следовательно, все точки, принадлежащие
множеству
,
удовлетворяют неравенству
имеет
вид:
.
Следовательно, все точки, принадлежащие
множеству
,
удовлетворяют неравенству ![]() ,
или
,
или ![]() .
Модуль комплексного числа
равен
.
Модуль комплексного числа
равен ![]() .
Тогда модуль комплексного числа
.
Тогда модуль комплексного числа ![]() равен
равен ![]() .
Следовательно, точки комплексной
плоскости, принадлежащие множеству
,
удовлетворяют условию
.
.
Следовательно, точки комплексной
плоскости, принадлежащие множеству
,
удовлетворяют условию
.
Тема: Дифференцирование функции комплексного переменного Если , то равно …
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
Решение: Производная функции равна . Тогда
Тема:
Дифференцирование функции комплексного
переменного
Значение
производной функции ![]() в
точке
равно
…
в
точке
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Производная
функции
имеет
вид![]() .
Тогда
.
Тогда 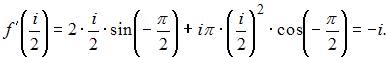
Тема: Операции над комплексными числами Произведение комплексных чисел
и равно
Тема:
Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
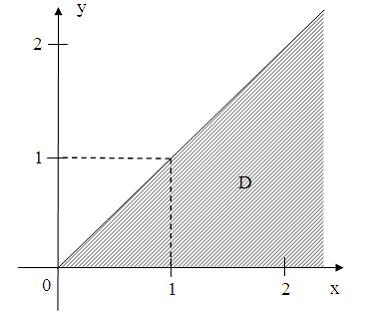 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Множество
,
изображенное на рисунке, ограничено
прямыми ![]() .
Для
комплексного числа
угол
наклона прямой
к
оси
равен
.
Следовательно, комплексные числа
,
принадлежащие множеству
,
должны удовлетворять условиям
.
Для
комплексного числа
угол
наклона прямой
к
оси
равен
.
Следовательно, комплексные числа
,
принадлежащие множеству
,
должны удовлетворять условиям
Тема:
Дифференцирование функции комплексного
переменного
Если
и ![]() ,
то мнимая часть производной этой
функции
имеет
вид …
,
то мнимая часть производной этой
функции
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Производная
функции ![]() равна
равна ![]() .
Тогда
.
Тогда ![]()
Тема: Операции над комплексными числами Дано комплексное число . Тогда равно 16
Тема: Дифференцирование функции комплексного переменного Значение производной функции в точке равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Производная функции имеет вид Тогда
Тема:
Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
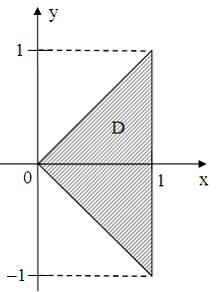 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Множество
,
изображенное на рисунке, ограничено
прямыми ![]() и
.
Для комплексного числа
угол
наклона прямой
к
оси
равен
,
а прямой
и
.
Для комплексного числа
угол
наклона прямой
к
оси
равен
,
а прямой ![]() ,
равен
,
равен ![]() .
Следовательно, комплексные числа
,
принадлежащие множеству
,
должны удовлетворять условиям
.
.
Следовательно, комплексные числа
,
принадлежащие множеству
,
должны удовлетворять условиям
.
Тема: Операции над комплексными числами Сумма комплексных чисел и равна …
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
Решение:
Чтобы
сложить два комплексных числа ![]() и
и ![]() ,
надо сложить их вещественные и мнимые
части, то есть
,
надо сложить их вещественные и мнимые
части, то есть ![]() .
В
нашем случае получим
.
В
нашем случае получим ![]() .
.
Тема:
Особые точки функции комплексного
переменного
Для
функции 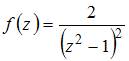 точка
точка ![]() является
…
является
…
|
|
|
полюсом второго порядка |
|
|
|
полюсом третьего порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение:
Порядок
полюса функции вида
равен
порядку нуля
.
Имеем 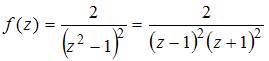 ,
поэтому
точка
будет
полюсом второго порядка.
,
поэтому
точка
будет
полюсом второго порядка.
Тема:
Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
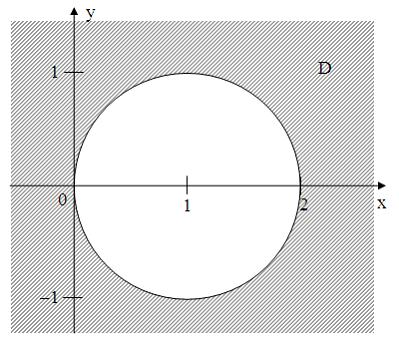 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Особые точки функции комплексного
переменного
Для
функции 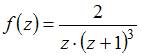 точка
точка ![]() является
…
является
…
|
|
|
полюсом третьего порядка |
|
|
|
полюсом второго порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение:
Порядок
полюса функции вида
равен
порядку нуля
.
Имеем 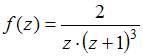 ,
поэтому
точка
будет
полюсом третьего порядка.
,
поэтому
точка
будет
полюсом третьего порядка.
Тема: Операции над комплексными числами Произведение комплексных чисел и равно …
Тема: Дифференцирование функции комплексного переменного Если и , то мнимая часть производной этой функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Операции над комплексными числами
Значение
выражения ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Области на комплексной плоскости Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Множество , изображенное на рисунке, ограничено прямыми и . Для комплексного числа угол наклона прямой к оси равен , а прямой , равен . Следовательно, комплексные числа , принадлежащие множеству , должны удовлетворять условиям .
Тема: Особые точки функции комплексного переменного Для функции точка является …
|
|
|
полюсом второго порядка |
|
|
|
полюсом третьего порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение: Порядок полюса функции вида равен порядку нуля . Имеем , поэтому точка будет полюсом второго порядка.
Тема:
Дифференцирование функции комплексного
переменного
Если
и ![]() ,
то действительная часть производной
этой функции
,
то действительная часть производной
этой функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Особые точки функции комплексного переменного Для функции точка является …
|
|
|
полюсом второго порядка |
|
|
|
полюсом третьего порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение: Порядок полюса функции вида равен порядку нуля . Так как , то точка будет полюсом второго порядка.
Тема:
Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
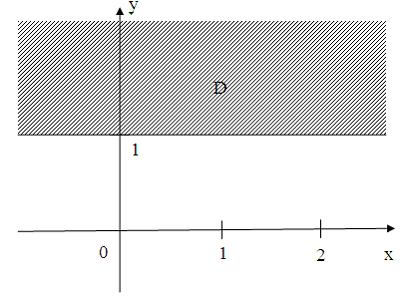 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
Тема:
Дифференцирование функции комплексного
переменного
Значение
производной функции ![]() в
точке
равно
…
в
точке
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Производная функции имеет вид
![]()
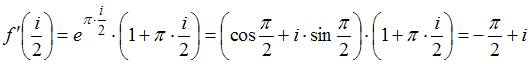
Видеоуроки ЕГЭ
Математика (1)
Информатика (2)
Физика (2)
Русский язык (0)
Обществознание (0)
История (0)
Английский язык (2)
Биология (0)
География (0)
Химия (0)
Экономика (1)
Разделы
Решебники
Презентации PowerPoint
Расчетки
Материалы
Шпаргалки
Лабораторные работы
Разное
Курсовые
Дипломы
Решение задач
Видеоуроки
СтудентLife
Новости
Юмор
Это интересно
ответы i-exam
Теория государства и права
Культурология
Метрология
Безопасность жизнедеятельности
Философия
Информатика
КП РФ
Политология
История
Материаловедение i-exam
Психология и педагогика
Математика
Отправка материалов!
Физика
|
ДЕ7.Дифференциальные уравнения
Тема:
Системы двух линейных дифференциальных
уравнений с постоянными коэффициентами
Общее
решение системы дифференциальных
уравнений 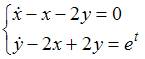 имеет
вид …
имеет
вид …![]()
Решение:
Решим
систему дифференциальных уравнений
методом исключения. Из первого уравнения
находим ![]() ,
откуда
,
откуда![]() После
подстановки во второе уравнение системы
получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами
После
подстановки во второе уравнение системы
получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами![]() Общее
решение этого уравнения имеет
вид
Общее
решение этого уравнения имеет
вид![]() где
где ![]() общее
решение соответствующего однородного
уравнения, а
общее
решение соответствующего однородного
уравнения, а ![]() некоторое
частное решение неоднородного
уравнения.
Характеристическое
уравнение
некоторое
частное решение неоднородного
уравнения.
Характеристическое
уравнение![]() имеет
два действительных корня
.Таким
корням соответствует общее решение
однородного дифференциального
уравнения
имеет
два действительных корня
.Таким
корням соответствует общее решение
однородного дифференциального
уравнения ![]() .Поскольку
правая часть исходного уравнения
.Поскольку
правая часть исходного уравнения ![]() ,
то имеем уравнение со специальной правой
частью.
Так как
не
является корнем характеристического
уравнения, то частное решение
,
то имеем уравнение со специальной правой
частью.
Так как
не
является корнем характеристического
уравнения, то частное решение![]() неоднородного
уравнения будем искать в виде
неоднородного
уравнения будем искать в виде ![]() Найдя
производные первого и второго порядков
и подставив в уравнение
,
получим
Найдя
производные первого и второго порядков
и подставив в уравнение
,
получим ![]() Тогда
общее решение исходного уравнения имеет
вид
Тогда
общее решение исходного уравнения имеет
вид ![]() Дифференцируя
полученное решение, находим
Дифференцируя
полученное решение, находим![]() и
и 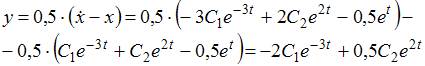 Значит,
общее решение системы уравнений имеет
вид
Значит,
общее решение системы уравнений имеет
вид
Тема:
Поле направлений и изоклины
Дано
дифференциальное уравнение
.
Тогда отрезок соответствующего ему
поля направлений в точке
образует
с осью
угол
при ![]() равном
равном ![]() 2.
2.
Решение:
Так
как дифференциальное уравнение имеет
вид
,
то угол![]() определяется
из равенства
,
где
-координаты
точки А.
определяется
из равенства
,
где
-координаты
точки А.
В рассматриваемом случае ,то есть . Следовательно
Тема:
Дифференциальные уравнения с разделяющимися
переменными
Общее
решение дифференциального уравнения![]() имеет
вид
имеет
вид ![]()
Решение:
Разделим
переменные: 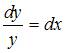 .
Проинтегрируем обе части
уравнения:
.
Проинтегрируем обе части
уравнения: 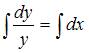 Тогда
Тогда ![]() .Откуда
.Откуда
Тема:
Задача Коши для дифференциального
уравнения первого порядка
Частное
решение дифференциального уравнения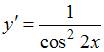 ,
удовлетворяющее условию
,
удовлетворяющее условию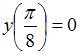 ,
имеет вид …
,
имеет вид …![]()
Решение:
Проинтегрируем
обе части уравнения: ![]() .
Подставив условие
,
получим
.
Подставив условие
,
получим ![]() и
и
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Общее решение системы дифференциальных уравнений имеет вид…
Решение:
Решим
систему дифференциальных уравнений
методом исключения.
Из второго
уравнения находим производную
и
после подстановки выражений для
и ![]() в
первое уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами
Характеристическое
уравнение
имеет
два действительных корня:
Таким
корням соответствует общее решение
однородного дифференциального
уравнения
.Дифференцируя
полученное решение, находим
Тогда
общее решение системы уравнений имеет
вид
.
в
первое уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами
Характеристическое
уравнение
имеет
два действительных корня:
Таким
корням соответствует общее решение
однородного дифференциального
уравнения
.Дифференцируя
полученное решение, находим
Тогда
общее решение системы уравнений имеет
вид
.
Тема:
Поле направлений и изоклины
Поле
направлений дифференциального
уравнения ![]() определяется
неравенством …
определяется
неравенством …
|
|
|
|
|
|
|
|
Тема:
Дифференциальные уравнения с разделяющимися
переменными
Дифференциальное
уравнение![]() будет
уравнением с разделяющимися переменными
при значении
будет
уравнением с разделяющимися переменными
при значении![]() ,
равном….. 4.
,
равном….. 4.
Решение:
Данное
уравнение можно представить в виде![]() .
Это уравнение будет уравнением с
разделяющимися переменными при
.
Это уравнение будет уравнением с
разделяющимися переменными при ![]() ,
то есть при
,
то есть при ![]() ,
откуда
,
откуда ![]()
Тема:
Задача Коши для дифференциального
уравнения первого порядка
Решение
задачи Коши ![]() имеет
вид …..
имеет
вид …..![]()
Решение:
Проинтегрировав
обе части уравнения, получим: ![]() .
Тогда общее решение исходного уравнения
имеет вид
.
Тогда общее решение исходного уравнения
имеет вид ![]() .
Для
вычисления значения
подставим
в найденное общее решение начальное
условие
.
Тогда
.
Для
вычисления значения
подставим
в найденное общее решение начальное
условие
.
Тогда ![]() и
и ![]() .
Следовательно,
частное решение имеет вид
.
Следовательно,
частное решение имеет вид
Тема: Дифференциальные уравнения с разделяющимися переменными Общее решение дифференциального уравнения имеет вид …
Решение:
Разделим
переменные: 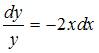 .
Проинтегрируем обе части уравнения:
.
Проинтегрируем обе части уравнения: 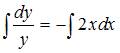 .
Тогда
.
Тогда ![]() ,
откуда
,
откуда
Тема:
Системы двух линейных дифференциальных
уравнений с постоянными коэффициентами
Общее
решение системы дифференциальных
уравнений 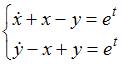 имеет
вид …
имеет
вид …![]()
Решение:
Решим
систему дифференциальных уравнений
методом исключения.
Из первого
уравнения находим ![]() ,
откуда
,
откуда ![]() .
После подстановки во второе уравнение
системы получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами
.
После подстановки во второе уравнение
системы получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами ![]() .Общее
решение этого уравнения имеет вид
,
где
.Общее
решение этого уравнения имеет вид
,
где ![]() –
общее решение соответствующего
однородного уравнения, а
–
общее решение соответствующего
однородного уравнения, а ![]() –
некоторое частное решение неоднородного
уравнения. Характеристическое
уравнение
–
некоторое частное решение неоднородного
уравнения. Характеристическое
уравнение ![]() имеет
два действительных корня:
имеет
два действительных корня: ![]() .
Таким корням соответствует общее решение
однородного дифференциального
уравнения
.
Таким корням соответствует общее решение
однородного дифференциального
уравнения ![]() .
Поскольку правая часть исходного
уравнения
.
Поскольку правая часть исходного
уравнения ![]() ,
то имеем уравнение со специальной правой
частью.
Так как
не
является корнем характеристического
уравнения, то частное решение
,
то имеем уравнение со специальной правой
частью.
Так как
не
является корнем характеристического
уравнения, то частное решение ![]() неоднородного
уравнения будем искать в виде
.
Найдя
производные первого и второго порядков
и подставив в уравнение
,
получим
неоднородного
уравнения будем искать в виде
.
Найдя
производные первого и второго порядков
и подставив в уравнение
,
получим ![]() .
Тогда общее решение исходного уравнения
имеет вид
.
Тогда общее решение исходного уравнения
имеет вид ![]() .
Дифференцируя
полученное решение, находим
.
Дифференцируя
полученное решение, находим ![]() и
и ![]() .
Следовательно,
общее решение системы уравнений имеет
вид
.
.
Следовательно,
общее решение системы уравнений имеет
вид
.
Тема:
Поле направлений и изоклины
Дано
дифференциальное уравнение 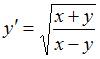 .
Тогда отрезок соответствующего ему
поля направлений в точке
.
Тогда отрезок соответствующего ему
поля направлений в точке ![]() образует
с осью
угол,
равный …
образует
с осью
угол,
равный …
Решение:
Так
как дифференциальное уравнение имеет
вид
,
то искомый угол
определяется
из равенства
,
где
–
координаты точки
.
В
рассматриваемом случае 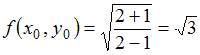 ,
то есть
,
то есть ![]() .
Следовательно,
.
Следовательно, ![]()
Тема:
Задача Коши для дифференциального
уравнения первого порядка
Решение
задачи Коши ![]() ,
имеет вид …
,
имеет вид …![]()
Решение:
Сделаем
замену ![]() .
Тогда
.
Тогда ![]() ,
, ![]() и
уравнение запишется в виде
и
уравнение запишется в виде ![]() .
Разделив переменные, получим:
.
Разделив переменные, получим:![]() .
Проинтегрируем обе части последнего
уравнения:
.
Проинтегрируем обе части последнего
уравнения: 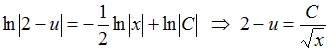 .
Сделаем
обратную замену:
.
Сделаем
обратную замену: ![]() ;
подставим в найденное общее решение
начальное условие
;
подставим в найденное общее решение
начальное условие ![]() .
Тогда
.
Тогда ![]() и
.
Следовательно,
частное решение имеет вид
и
.
Следовательно,
частное решение имеет вид
Тема:
Системы двух линейных дифференциальных
уравнений с постоянными коэффициентами
Решение
задачи Коши 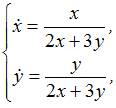
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выразив ![]() из
первого уравнения, можем получить
из
первого уравнения, можем получить 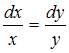 ,
откуда
,
откуда ![]() .
Сложив удвоенное первое и утроенное
второе уравнения, получим
.
Сложив удвоенное первое и утроенное
второе уравнения, получим ![]() ,
или
,
или ![]() ,
то есть
,
то есть ![]() .
Из системы уравнений
.
Из системы уравнений 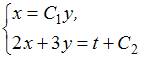 находим
общее решение системы
находим
общее решение системы 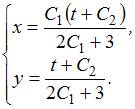 Подставив
начальные условия, получим:
Подставив
начальные условия, получим: 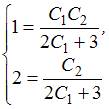
![]()
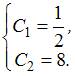 .Поэтому
решение задачи Коши имеет вид
.Поэтому
решение задачи Коши имеет вид ![]()
Тема: Поле направлений и изоклины Дано дифференциальное уравнение . Тогда отрезок соответствующего ему поля направлений в точке образует с осью угол при равном…
|
|
|
2 |
|
|
|
14 |
|
|
|
|
|
|
|
|
Решение: Так как дифференциальное уравнение имеет вид , то угол определяется из равенства , где – координаты точки . В рассматриваемом случае , то есть . Следовательно,
Тема:
Поле направлений и изоклины
Дано
дифференциальное уравнение ![]() .
Тогда отрезок соответствующего ему
поля направлений в точке
.
Тогда отрезок соответствующего ему
поля направлений в точке ![]() образует
с осью
образует
с осью ![]() угол
угол ![]() при
равном
…
при
равном
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Данное
уравнение можно представить в виде ![]() .
Действительно,
.
Действительно, 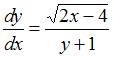 ,
или
,
или 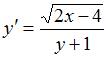 .
Тогда угол
определяется
из равенства
.
Тогда угол
определяется
из равенства ![]() ,
где
,
где ![]() –
координаты точки
.
В
рассматриваемом случае
–
координаты точки
.
В
рассматриваемом случае 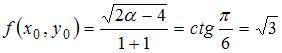 ,
то есть
,
то есть ![]() .
Следовательно,
.
Следовательно, ![]()
Тема: Задача Коши для дифференциального уравнения первого порядка Функция является общим решением дифференциального уравнения 1-го порядка. Тогда для начального условия частное решение этого уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Подставив
в общее решение начальное условие
,
то есть ![]() ,
получим значение
.
Следовательно,
искомое частное решение имеет вид
,
получим значение
.
Следовательно,
искомое частное решение имеет вид
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Решение задачи Коши , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Поле направлений и изоклины Дано дифференциальное уравнение . Тогда отрезок соответствующего ему поля направлений в точке образует с осью угол, равный …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как дифференциальное уравнение имеет
вид
,
то искомый угол
определяется
из равенства
,
где
–
координаты точки
.
В рассматриваемом случае ![]() ,
то есть
,
то есть ![]() .
Следовательно,
.
Следовательно, ![]() .
.
Тема: Задача Коши для дифференциального уравнения первого порядка Решение задачи Коши , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Сделаем замену . Тогда , и уравнение запишется в виде . Разделив переменные, получим: . Проинтегрируем обе части последнего уравнения: . Сделаем обратную замену: ; подставим в найденное общее решение начальное условие . Тогда и . Следовательно, частное решение имеет вид .
Тема: Дифференциальные уравнения с разделяющимися переменными Общее решение дифференциального уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Разделим переменные: . Проинтегрируем обе части уравнения: . Тогда . Откуда
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Решение задачи Коши , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Дифференциальные уравнения с разделяющимися
переменными
Общее
решение дифференциального уравнения 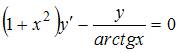 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Разделим
переменные: 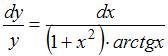 .
Проинтегрируем обе части уравнения:
.
Проинтегрируем обе части уравнения: 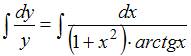 .
Тогда
.
Тогда ![]() .
Откуда
.
.
Откуда
.
Тема: Задача Коши для дифференциального уравнения первого порядка Частное решение дифференциального уравнения , удовлетворяющее условию , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Проинтегрируем
обе части уравнения: ![]() .
Подставив начальное условие
,
получим
и
.
Подставив начальное условие
,
получим
и ![]() .
.
Тема: Поле направлений и изоклины Поле направлений дифференциального уравнения определяется неравенством …
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Общее решение системы дифференциальных уравнений имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Решим систему дифференциальных уравнений методом исключения. Из второго уравнения находим производную и после подстановки выражений для и в первое уравнение системы получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами . Характеристическое уравнение имеет два действительных корня: . Таким корням соответствует общее решение однородного дифференциального уравнения . Дифференцируя полученное решение, находим . Тогда общее решение системы уравнений имеет вид
Тема: Задача Коши для дифференциального уравнения первого порядка Частное решение дифференциального уравнения , удовлетворяющее условию , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Введем замену ; . Тогда уравнение примет вид , или . Пусть . Тогда . Подставим найденное значение в уравнение . Получим: , то есть и . Общее решение примет вид . Подставив начальное условие, получим . Откуда и частное решение будет иметь вид .
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Общее решение системы дифференциальных уравнений имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решим
систему дифференциальных уравнений
методом исключения.
Из первого
уравнения находим производную ![]() и
после подстановки выражений для
и
и
после подстановки выражений для
и ![]() во
второе уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами
во
второе уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами ![]() .
Характеристическое уравнение
.
Характеристическое уравнение ![]() имеет
два действительных корня:
имеет
два действительных корня: ![]() .
Таким
корням соответствует общее решение
однородного дифференциального
уравнения
.
Таким
корням соответствует общее решение
однородного дифференциального
уравнения ![]() .
Дифференцируя
полученное решение, находим
.
Дифференцируя
полученное решение, находим ![]() .
Тогда
общее решение системы уравнений имеет
вид
.
Тогда
общее решение системы уравнений имеет
вид ![]() .
.
Тема: Дифференциальные уравнения с разделяющимися переменными Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …
|
|
|
, |
|
|
|
, |
|
|
|
|
|
|
|
, |
Решение:
Угловой
коэффициент касательной в произвольной
точке равен производной в этой точке,
то есть ![]() ,
а угловой коэффициент радиус-вектора
точки касания определяется отношением
,
а угловой коэффициент радиус-вектора
точки касания определяется отношением ![]() .
Тогда для нахождения уравнения искомой
кривой получим уравнение с разделяющимися
переменными
.
Тогда для нахождения уравнения искомой
кривой получим уравнение с разделяющимися
переменными ![]() .
Разделив переменные, получим
.
Разделив переменные, получим 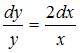 .
Проинтегрируем обе части этого
уравнения:
.
Проинтегрируем обе части этого
уравнения: 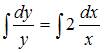 .
Тогда
.
Тогда ![]() ,
.
Откуда
,
.
,
.
Откуда
,
.
Тема: Поле направлений и изоклины Дано дифференциальное уравнение . Тогда отрезок соответствующего ему поля направлений в точке образует с осью угол, равный …
Тема: Дифференциальные уравнения с разделяющимися переменными Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …
|
|
|
, |
|
|
|
, |
|
|
|
|
|
|
|
, |
Решение: Угловой коэффициент касательной в произвольной точке равен производной в этой точке, то есть , а угловой коэффициент радиус-вектора точки касания определяется отношением . Тогда для нахождения уравнения искомой кривой получим уравнение с разделяющимися переменными . Разделив переменные, получим . Проинтегрируем обе части этого уравнения: . Тогда , . Откуда , .
Тема: Задача Коши для дифференциального уравнения первого порядка Частное решение дифференциального уравнения , удовлетворяющее условию , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Проинтегрируем обе части уравнения: . Подставив начальное условие , получим и
ДЕ8.Теория вероятности
Тема:
Числовые характеристики случайных
величин
Дискретная
случайная величина X задана
законом распределения вероятностей:  Тогда
ее среднее квадратическое отклонение
равно …
0,80
Тогда
ее среднее квадратическое отклонение
равно …
0,80
Решение:
Среднее
квадратическое отклонение случайной
величины Х определяется как ![]() ,
где дисперсию дискретной случайной
величины можно вычислить по формуле
,
где дисперсию дискретной случайной
величины можно вычислить по формуле![]() .Тогда
.Тогда ![]() ,
а
,
а ![]()
Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
|
|
|
|
Тема: Полная вероятность. Формулы Байеса В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
Решение: Для вычисления вероятности события A (вынутый наудачу шар – черный) применим формулу полной вероятности: .Здесь вероятность того, что из первой урны переложили во вторую урну белый шар; – вероятность того, что из первой урны переложили во вторую урну черный шар; – условная вероятность того, что вынутый шар черный, если из первой урны во вторую был переложен белый шар; – условная вероятность того, что вынутый шар черный, если из первой урны во вторую был переложен черный шар.
![]()
Тема: Законы распределения вероятностей дискретных случайных величин Дискретная случайная величина Х задана законом распределения вероятностей: Тогда вероятность равна …
|
|
|
0,8 |
Решение: ![]()
Тема:
Числовые характеристики случайных
величин
Дисперсия
дискретной случайной величины Х, заданной
законом распределения вероятностей: 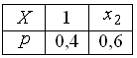 равна
0,06. Тогда значение
равна
0,06. Тогда значение ![]() равно
…
равно
…
|
|
|
1,5 |
Решение: Дисперсию дискретной случайной величины можно вычислить по формуле . Тогда
![]() или
или ![]() .
Решив последнее уравнение, получаем
два корня
.
Решив последнее уравнение, получаем
два корня![]() и
и ![]()
Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
|
|
|
|
Решение:
Для
вычисления события А (среди отобранных
деталей нет годных) воспользуемся
формулой ![]() где n –
общее число возможных элементарных
исходов испытания, а m –
число элементарных исходов,
благоприятствующих появлению события
А. нашем случае общее число возможных
элементарных исходов равно числу
способов, которыми можно извлечь три
детали из 12 имеющих, то есть
где n –
общее число возможных элементарных
исходов испытания, а m –
число элементарных исходов,
благоприятствующих появлению события
А. нашем случае общее число возможных
элементарных исходов равно числу
способов, которыми можно извлечь три
детали из 12 имеющих, то есть ![]() .
.
А
общее число благоприятствующих исходов
равно числу способов, которыми можно
извлечь три бракованные детали из пяти,
то есть ![]() .
. 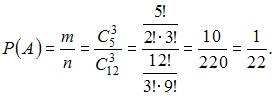
Тема: Полная вероятность. Формулы Байеса Банк выдает 44% всех кредитов юридическим лицам, а 56% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,2; а для физического лица эта вероятность составляет 0,1. Тогда вероятность того, что очередной кредит будет погашен в срок, равна …
|
|
|
0,856 |
Решение:
Для
вычисления вероятности события A (выданный
кредит будет погашен в срок) применим
формулу полной вероятности:
.
Здесь
–
вероятность того, что кредит был выдан
юридическому лицу;
–
вероятность того, что кредит был выдан
физическому лицу;
–
условная вероятность того, что кредит
будет погашен в срок, если он был выдан
юридическому лицу;
–
условная вероятность того, что кредит
будет погашен в срок, если он был выдан
физическому лицу. Тогда![]()
Тема:
Законы распределения вероятностей
дискретных случайных величин
Для
дискретной случайной величины Х  функция
распределения вероятностей имеет вид:
функция
распределения вероятностей имеет вид: 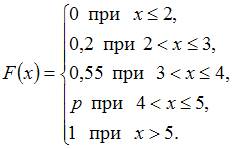
Тогда
значение параметра ![]() может
быть равно …
может
быть равно …
|
|
|
0,655 |
Тема: Определение вероятности Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Решение: Для вычисления события (сумма выпавших очков будет не меньше девяти) воспользуемся формулой , где – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны элементарных исходов испытания, из которых благоприятствующими являются исходы вида , , , , , , , и , то есть . Следовательно,
Тема:
Законы распределения вероятностей
дискретных случайных величин
Для
дискретной случайной величины
:
 функция
распределения вероятностей имеет
вид:
функция
распределения вероятностей имеет
вид:
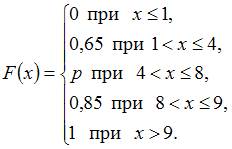 Тогда
значение параметра
может
быть равно …
Тогда
значение параметра
может
быть равно …
|
|
|
0,7 |
|
|
|
1 |
|
|
|
0,85 |
|
|
|
0,6 |
Решение:
По
определению
.
Следовательно, ![]() и
и ![]() .
Этим условиям удовлетворяет, например,
значение
.
Этим условиям удовлетворяет, например,
значение![]()
Тема:
Числовые характеристики случайных
величин
Непрерывная
случайная величина
задана
функцией распределения вероятностей:
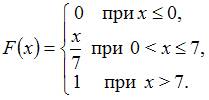 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Эта
случайная величина распределена
равномерно в интервале ![]() .
Тогда ее дисперсию можно вычислить по
формуле
.
Тогда ее дисперсию можно вычислить по
формуле 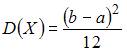 .
То есть
.
То есть 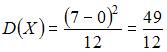
Тема: Полная вероятность. Формулы Байеса В первой урне 6 черных шаров и 4 белых шара. Во второй урне 2 белых и 8 черных шаров. Из наудачу взятой урны вынули один шар, который оказался белым. Тогда вероятность того, что этот шар вынули из первой урны, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Предварительно
вычислим вероятность события A (вынутый
наудачу шар – белый) по формуле полной
вероятности:
.
Здесь
–
вероятность того, что шар извлечен из
первой урны;
–
вероятность того, что шар извлечен из
второй урны;
–
условная вероятность того, что вынутый
шар белый, если он извлечен из первой
урны;
–
условная вероятность того, что вынутый
шар белый, если он извлечен из второй
урны.
Тогда ![]() .
Теперь
вычислим условную вероятность того,
что этот шар был извлечен из первой
урны, по формуле Байеса:
.
Теперь
вычислим условную вероятность того,
что этот шар был извлечен из первой
урны, по формуле Байеса: 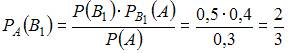
Тема: Числовые характеристики случайных величин Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее дисперсия равна …
|
|
|
7,56 |
|
|
|
3,2 |
|
|
|
3,36 |
|
|
|
6,0 |
Решение: Дисперсию дискретной случайной величины можно вычислить по формуле
.
Тогда ![]()
Тема:
Законы распределения вероятностей
дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
ее функция распределения вероятностей
имеет вид …
Тогда
ее функция распределения вероятностей
имеет вид …
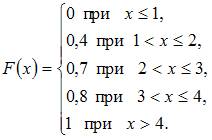
Решение:
По
определению
.
Тогда
а) при ![]() ,
, ![]() ,
б)
при
,
б)
при ![]() ,
, ![]() ,
в)
при
,
в)
при ![]() ,
, ![]() ,
г)
при
,
г)
при ![]() ,
, ![]() ,
д)
при
,
д)
при ![]() ,
, ![]() .
Следовательно,
.
Следовательно,
Тема: Определение вероятности Внутрь круга радиуса 4 наудачу брошена точка. Тогда вероятность того, что точка окажется вне вписанного в круг квадрата, равна …
|
|
|
|
Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
вычисления события ![]() (среди
отобранных деталей нет бракованных)
воспользуемся формулой
,
где n –
общее число возможных элементарных
исходов испытания, а m –
число элементарных исходов,
благоприятствующих появлению события
.
В нашем случае общее число возможных
элементарных исходов равно числу
способов, которыми можно извлечь три
детали из 12 имеющих, то есть
.
А общее число благоприятствующих исходов
равно числу способов, которыми можно
извлечь три небракованные детали из
семи, то есть
(среди
отобранных деталей нет бракованных)
воспользуемся формулой
,
где n –
общее число возможных элементарных
исходов испытания, а m –
число элементарных исходов,
благоприятствующих появлению события
.
В нашем случае общее число возможных
элементарных исходов равно числу
способов, которыми можно извлечь три
детали из 12 имеющих, то есть
.
А общее число благоприятствующих исходов
равно числу способов, которыми можно
извлечь три небракованные детали из
семи, то есть ![]() .
Следовательно,
.
Следовательно, 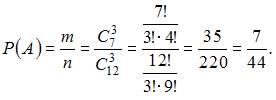
Тема: Полная вероятность. Формулы Байеса Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …
|
|
|
0,57 |
|
|
|
0,43 |
|
|
|
0,55 |
|
|
|
0,53 |
Решение:
Для
вычисления вероятности события A (вынутый
наудачу шар – белый) применим формулу
полной вероятности:
.
Здесь
–
вероятность того, что шар извлечен из
первой серии урн;
–
вероятность того, что шар извлечен из
второй серии урн;
–
условная вероятность того, что вынутый
шар белый, если из он извлечен из первой
серии урн;
–
условная вероятность того, что вынутый
шар белый, если из он извлечен из второй
серии урн.
Тогда![]()
Тема:
Законы распределения вероятностей
дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
![]() Тогда
вероятность
Тогда
вероятность ![]() равна
…
равна
…
|
|
|
0,5 |
|
|
|
0,8 |
|
|
|
0,7 |
|
|
|
0,1 |
ЗАДАНИЕ N 40 сообщить об ошибке Тема: Числовые характеристики случайных величин Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
Решение:
Воспользуемся
формулой 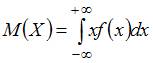 .
Тогда
.
Тогда 
Тема: Полная вероятность. Формулы Байеса Банк выдает 70% всех кредитов юридическим лицам, а 30% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило юридическое лицо, равна …
|
|
|
0,875 |
|
|
|
0,125 |
|
|
|
0,105 |
|
|
|
0,375 |
Решение:
Предварительно
вычислим вероятность события A (выданный
кредит не будет погашен в срок) по формуле
полной вероятности:
.
Здесь
–
вероятность того, что кредит был выдан
юридическому лицу;
–
вероятность того, что кредит был выдан
физическому лицу;
–
условная вероятность того, что кредит
не будет погашен в срок, если он был
выдан юридическому лицу;
–
условная вероятность того, что кредит
не будет погашен в срок, если он был
выдан физическому лицу. Тогда
![]() .
Теперь
вычислим условную вероятность того,
что этот кредит не погасило юридическое
лицо, по формуле Байеса:
.
Теперь
вычислим условную вероятность того,
что этот кредит не погасило юридическое
лицо, по формуле Байеса:
 .
.
Тема: Числовые характеристики случайных величин Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
Решение: Воспользуемся формулой . Тогда .
Тема: Определение вероятности В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
вычисления вероятности искомого события
воспользуемся формулой 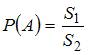 ,
где
,
где ![]() –
площадь меньшего круга, а
–
площадь меньшего круга, а ![]() –
площадь большего круга. Следовательно,
–
площадь большего круга. Следовательно, 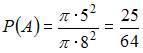
Тема:
Числовые характеристики случайных
величин
Непрерывная
случайная величина
задана
плотностью распределения вероятностей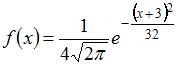 .
Тогда математическое ожидание a и
среднее квадратическое отклонение
этой
случайной величины равны …
.
Тогда математическое ожидание a и
среднее квадратическое отклонение
этой
случайной величины равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Плотность
распределения вероятностей нормально
распределенной случайной величины
имеет
вид 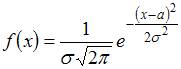 ,
где
,
где ![]() ,
, ![]() .
Поэтому
.
.
Поэтому
.
Тема: Законы распределения вероятностей дискретных случайных величин Дискретная случайная величина задана законом распределения вероятностей: Тогда значения a и b могут быть равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как сумма вероятностей возможных
значений
равна
1, то ![]() .
Этому условию удовлетворяет ответ:
.
.
Этому условию удовлетворяет ответ:
.
Тема: Определение вероятности В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Для вычисления вероятности искомого события воспользуемся формулой , где – площадь меньшего круга, а – площадь большего круга. Следовательно, .
Тема: Полная вероятность. Формулы Байеса В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 5 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет белым, равна …
|
|
|
0,47 |
|
|
|
0,55 |
|
|
|
0,35 |
|
|
|
0,50 |
Решение:
Для
вычисления вероятности события A (вынутый
наудачу шар – белый) применим формулу
полной вероятности:
.
Здесь
–
вероятность того, что из первой урны
переложили во вторую урну белый шар;
–
вероятность того, что из первой урны
переложили во вторую урну черный шар;
–
условная вероятность того, что вынутый
шар белый, если из первой урны во вторую
был переложен белый шар;
–
условная вероятность того, что вынутый
шар белый, если из первой урны во вторую
был переложен черный шар.
Тогда ![]()
Тема: Законы распределения вероятностей дискретных случайных величин Для дискретной случайной величины : функция распределения вероятностей имеет вид: Тогда значение параметра может быть равно …
|
|
|
0,7 |
|
|
|
1 |
|
|
|
0,85 |
|
|
|
0,6 |
ЗАДАНИЕ N 10 сообщить об ошибке Тема: Полная вероятность. Формулы Байеса Банк выдает 70% всех кредитов юридическим лицам, а 30% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило юридическое лицо, равна …
|
|
|
0,875 |
|
|
|
0,125 |
|
|
|
0,105 |
|
|
|
0,375 |
Решение: Предварительно вычислим вероятность события A (выданный кредит не будет погашен в срок) по формуле полной вероятности: . Здесь – вероятность того, что кредит был выдан юридическому лицу; – вероятность того, что кредит был выдан физическому лицу; – условная вероятность того, что кредит не будет погашен в срок, если он был выдан юридическому лицу; – условная вероятность того, что кредит не будет погашен в срок, если он был выдан физическому лицу. Тогда . Теперь вычислим условную вероятность того, что этот кредит не погасило юридическое лицо, по формуле Байеса: .
ЗАДАНИЕ N 11 сообщить об ошибке Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Для вычисления события (среди отобранных деталей нет годных) воспользуемся формулой , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события . В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть . А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три бракованные детали из пяти, то есть . Следовательно,
ЗАДАНИЕ
N 12 сообщить
об ошибке
Тема:
Числовые характеристики случайных
величин
Непрерывная
случайная величина
задана
плотностью распределения вероятностей:
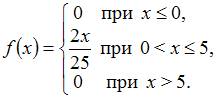 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Дисперсию непрерывной случайной величины можно вычислить по формуле
Тогда 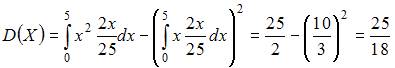
Тема: Законы распределения вероятностей дискретных случайных величин Дискретная случайная величина задана законом распределения вероятностей: Тогда ее функция распределения вероятностей имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
По
определению
.
Тогда
а) при
,
,
б)
при
,
,
в)
при
,
,
г)
при
,
,
д)
при
,
.
Следовательно, 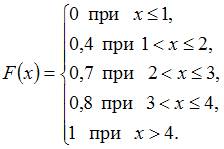
Тема: Полная вероятность. Формулы Байеса Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …
|
|
|
0,57 |
|
|
|
0,43 |
|
|
|
0,55 |
|
|
|
0,53 |
Решение: Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности: . Здесь – вероятность того, что шар извлечен из первой серии урн; – вероятность того, что шар извлечен из второй серии урн; – условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн; – условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн. Тогда .
Тема: Законы распределения вероятностей дискретных случайных величин Дискретная случайная величина задана законом распределения вероятностей: Тогда вероятность равна …
|
|
|
0,8 |
|
|
|
0,3 |
|
|
|
0,7 |
|
|
|
0,4 |
Решение: .
Тема: Числовые характеристики случайных величин Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее дисперсия равна …
|
|
|
7,56 |
|
|
|
3,2 |
|
|
|
3,36 |
|
|
|
6,0 |
Тема: Определение вероятности Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Решение:
Для
вычисления события
(сумма
выпавших очков будет равна десяти)
воспользуемся формулой
,
где
–
общее число возможных элементарных
исходов испытания, а m –
число элементарных исходов,
благоприятствующих появлению события A.
В нашем случае возможны
элементарных
исходов испытания, из которых
благоприятствующими являются исходы
вида
,
и ![]() ,
то есть
,
то есть ![]() .
Следовательно,
.
Следовательно, ![]()
ДЕ9. Математическая статистика
1)Тема:
Интервальные оценки параметров
распределения
Дан
доверительный интервал![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна … 36,62
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна … 36,62
Решение:
Интервальная
оценка математического ожидания
нормально распределенного количественного
признака представляет собой интервал,
симметричный относительно точечной
оценки. Тогда точечная оценка будет
равна ![]()
Тема:
Проверка статистических гипотез
Соотношением
вида![]() можно
определить …
можно
определить …
|
|
|
левостороннюю критическую область |
Тема:
Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии![]() на
на ![]() имеет
вид
.
имеет
вид
.
Тогда выборочный коэффициент корреляции может быть равен …
|
|
|
|
Решение:
Значение
выборочного коэффициента корреляции,
во-первых, принадлежит промежутку![]() а
во-вторых, его знак совпадает со знаком
выборочного коэффициента регрессии.
Этим условиям удовлетворяет значение
а
во-вторых, его знак совпадает со знаком
выборочного коэффициента регрессии.
Этим условиям удовлетворяет значение![]()
Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема
гистограмма частот которой имеет вид:
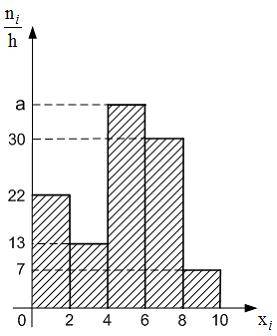
Тогда значение a равно …
|
|
|
38 |
Решение:
Так
как объем выборки вычисляется как ![]() где
где ![]() то
то
![]()
Тема: Интервальные оценки параметров распределения Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Проверка статистических гипотез
Основная
гипотеза имеет вид ![]() .
Тогда конкурирующей может являться
гипотеза …
.
Тогда конкурирующей может являться
гипотеза …![]()
Решение:
Конкурирующей
(альтернативной) называют гипотезу,
которая противоречит основной гипотезе.
Условию![]() противоречит
противоречит ![]() .
.
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема ![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:

Тогда
относительная частота варианты ![]() в
выборке равна …
0,05
в
выборке равна …
0,05
Решение:
Относительная
частота ![]() вычисляется
по формуле
вычисляется
по формуле 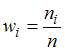 ,
где
,
где ![]() –
частота варианты
–
частота варианты![]() ,
а
,
а 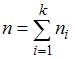 –
объем выборки. Вычислим предварительно
частоту варианты
–
объем выборки. Вычислим предварительно
частоту варианты ![]() как
как ![]() .
Тогда
.
Тогда ![]()
Тема:
Интервальные оценки параметров
распределения
Дан
доверительный интервал ![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении надежности
(доверительной вероятности) оценки
доверительный интервал может принять
вид …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении надежности
(доверительной вероятности) оценки
доверительный интервал может принять
вид …
|
|
|
|
Решение:
Доверительный
интервал для оценки математического
ожидания нормально распределенного
количественного признака можно
представить в виде симметричного
интервала ![]() ,
где точечная оценка математического
ожидания
,
где точечная оценка математического
ожидания ![]() ,
а точность оценки
,
а точность оценки ![]() .
В случае увеличения надежности точность
оценки ухудшается, то есть значение
будет
больше 0,77.
.
В случае увеличения надежности точность
оценки ухудшается, то есть значение
будет
больше 0,77.
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема

Тогда
относительная частота варианты ![]() равна
…
равна
…
|
|
|
0,25 |
Тема:
Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид ![]() .
Тогда выборочное среднее признака
равно
…
.
Тогда выборочное среднее признака
равно
…![]()
Тема: Проверка статистических гипотез Левосторонняя критическая область может определяться из соотношения …
Решение:
Левосторонней
называют критическую область, определяемую
соотношением ![]() ,
где
,
где ![]() –
отрицательное число, а
–
уровень значимости. Таким соотношением
является
–
отрицательное число, а
–
уровень значимости. Таким соотношением
является
Тема: Проверка статистических гипотез Двусторонняя критическая область может определяться из соотношения …
![]()
Тема: Интервальные оценки параметров распределения Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид …
|
|
|
|
Тема: Интервальные оценки параметров распределения Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Доверительный
интервал для оценки математического
ожидания нормально распределенного
количественного признака можно
представить в виде симметричного
интервала
,
где точечная оценка математического
ожидания ![]() ,
а точность оценки
,
а точность оценки ![]() .
Следовательно,
интервальная оценка будет иметь вид
.
Следовательно,
интервальная оценка будет иметь вид
Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема , гистограмма относительных частот которой имеет вид
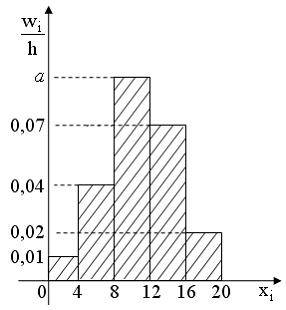
Тогда значение a равно …
![]()
Тема: Проверка статистических гипотез Соотношением вида можно определить …
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
Решение:
Данное
соотношение определяет правостороннюю
критическую область, так как правосторонней
называют критическую область, определяемую
соотношением вида ![]() ,
где
–
положительное число, а
–
уровень значимости.
,
где
–
положительное число, а
–
уровень значимости.
Тема: Проверка статистических гипотез Левосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы корреляционного анализа Выборочное уравнение прямой линии регрессии на имеет вид . Тогда выборочное среднее признака равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выборочное
уравнение прямой линии регрессии
на
имеет
вид ![]() .
Тогда выборочное среднее признака
равно
.
Тогда выборочное среднее признака
равно ![]() .
.
Тема:
Интервальные оценки параметров
распределения
Дан
доверительный интервал ![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
|
|
|
1,12 |
|
|
|
0,01 |
|
|
|
2,24 |
|
|
|
13,56 |
Тема: Статистическое распределение выборки Статистическое распределение выборки имеет вид Тогда значение относительной частоты равно …
|
|
|
0,25 |
|
|
|
0,05 |
|
|
|
0,26 |
|
|
|
0,75 |
Решение:
Сумма
относительных частот равна единице.
Поэтому ![]() .
.
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Решение задачи Коши , имеет вид …
Тема: Элементы корреляционного анализа Выборочное уравнение прямой линии регрессии на имеет вид . Тогда выборочное среднее признака равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Интервальные оценки параметров распределения Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала , где точечная оценка математического ожидания , а точность оценки . В случае увеличения надежности точность оценки ухудшается, то есть значение будет больше 0,77.
Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема : Тогда относительная частота варианты равна …
|
|
|
0,25 |
|
|
|
0,75 |
|
|
|
0,24 |
|
|
|
0,04 |
Тема:
Проверка статистических гипотез
Соотношением
вида ![]() можно
определить …
можно
определить …
|
|
|
двустороннюю критическую область |
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
область принятия гипотезы |
Решение:
Данное
соотношение определяет двустороннюю
критическую область, так как двусторонней
называют критическую область, определяемую,
например, соотношением вида ![]() ,
где
–
положительное число, а
–
уровень значимости.
,
где
–
положительное число, а
–
уровень значимости.
Тема:
Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид ![]() ,
а выборочные средние квадратические
отклонения равны:
,
а выборочные средние квадратические
отклонения равны: ![]() .
Тогда выборочный коэффициент
корреляции
.
Тогда выборочный коэффициент
корреляции ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выборочный
коэффициент корреляции ![]() можно
вычислить из соотношения
можно
вычислить из соотношения 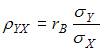 .
Тогда
.
Тогда 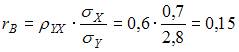 .
.
Тема: Проверка статистических гипотез Соотношением вида можно определить …
|
|
|
двустороннюю критическую область |
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
область принятия гипотезы |
Тема: Интервальные оценки параметров распределения Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
|
|
|
36,62 |
|
|
|
36,52 |
|
|
|
9,12 |
|
|
|
73,24 |
Решение: Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна .
Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема , полигон относительных частот которой имеет вид: Тогда число вариант в выборке равно …
|
|
|
37 |
|
|
|
63 |
|
|
|
100 |
|
|
|
36 |
Решение:
Вычислим
предварительно относительную частоту
варианты
как ![]() .
Тогда из определения относительной
частоты
.
Тогда из определения относительной
частоты ![]() ,
получаем, что
,
получаем, что![]()
Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид: Тогда число вариант в выборке равно …
|
|
|
32 |
|
|
|
82 |
|
|
|
8 |
|
|
|
31 |
Тема: Проверка статистических гипотез Соотношением вида можно определить …
|
|
|
двустороннюю критическую область |
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
область принятия гипотезы |
Тема: Интервальные оценки параметров распределения Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
|
|
|
36,62 |
|
|
|
36,52 |
|
|
|
9,12 |
|
|
|
73,24 |
Тема: Элементы корреляционного анализа При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии на равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Выборочный коэффициент регрессии на вычисляется по формуле . Тогда
Тема:
Статистическое распределение
выборки
Статистическое
распределение выборки имеет вид
 Тогда
объем выборки равен …
Тогда
объем выборки равен …
|
|
|
67 |
|
|
|
40 |
|
|
|
5 |
|
|
|
107 |
Решение:
Объем
выборки вычисляется по формуле
,
где ![]() –
частота варианты
–
частота варианты ![]() .
Тогда
.
Тогда ![]() .
.
Тема: Проверка статистических гипотез Соотношением вида можно определить …
|
|
|
левостороннюю критическую область |
|
|
|
правостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
Решение:
Данное
соотношение определяет левостороннюю
критическую область, так как левосторонней
называют критическую область, определяемую
соотношением ![]() ,
где
–
положительное число, а
–
уровень значимости.
,
где
–
положительное число, а
–
уровень значимости.
ДЕ-10 Элементы комбинаторики
Тема: Элементы комбинаторики Сколько чисел меньших, чем миллион можно написать с помощью цифр 3 и 7?
|
126 | |
Решение:
С
помощью двух различных цифр можно
записать![]() –
шестизначных чисел, ,
–
шестизначных чисел, , ![]() –
пятизначных ,
–
пятизначных , ![]() -
четырехзначных
-
четырехзначных ![]() трехзначных
чисел
трехзначных
чисел![]() двузначных
чисел,
двузначных
чисел, ![]() –
однозначных чисел. Просуммируем эти
композиции
–
однозначных чисел. Просуммируем эти
композиции 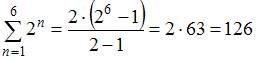
Тема:
Неориентированные графы
Матрица
смежности графа, изображенного на
рисунке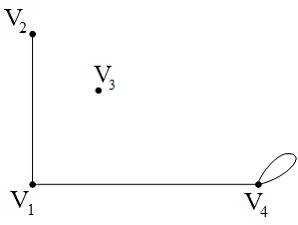
имеет
вид …
Решение:
Матрицей смежности графа называют
квадратную матрицу![]() размера
размера![]() ,
строкам и столбцам которой соответствуют
вершины помеченного графа (первый
столбец (строка) отвечает первой вершине
и т.д.), а ее элементы
,
строкам и столбцам которой соответствуют
вершины помеченного графа (первый
столбец (строка) отвечает первой вершине
и т.д.), а ее элементы![]() равны
количеству ребер, инцидентных вершинам
с номерами i и j.
Согласно определению составляем матрицу
смежности
равны
количеству ребер, инцидентных вершинам
с номерами i и j.
Согласно определению составляем матрицу
смежности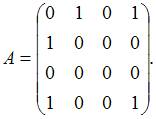
Тема: Операции над высказываниями Нулевой набор у формулы получается при следующих значениях переменных … ,
Тема: Декартово произведение множеств Пусть заданы два множества: ,
Тогда геометрическая интерпретация множества имеет вид …
Тема: Элементы комбинаторики Вокруг костра сидят 12 разбойников. Каждый из них смертельно ненавидит двух ближайших соседей. С целью спрятать награбленное необходимо выделить 5 разбойников. Сколькими способами атаман может назначить пятерых так, чтобы между ними не было распрей?
|
12 | |
Решение:
12
разбойников разбиваются на две группы
по 6 не враждующих между собой человек.
Атаман может выбрать 5 человек из первой
группы![]() способами
или 5 человек из второй группы
тоже
способами.
Тогда по правилу суммы получим:
способами
или 5 человек из второй группы
тоже
способами.
Тогда по правилу суммы получим:![]() способов
выбора 5 разбойников.
способов
выбора 5 разбойников.
Тема:
Операции над высказываниями
Отрицание
высказывания![]() равносильно
высказыванию …
равносильно
высказыванию …![]()
Решение:
Высказывание ![]() означает:
неправда что х положительно, а значит
означает:
неправда что х положительно, а значит
Тема: Неориентированные графы Эйлеровым является граф …

Решение: Эйлеровым называют граф содержащий эйлеров цикл. Цикл называется эйлеровым, если он простой и содержит все ребра графа. Критерий эйлеровости графа: граф называется Эйлеровым тогда и только тогда, когда степени всех его вершин четные. Из представленных графов только этот граф имеет четные степени всех вершин.
Тема:
Декартово произведение множеств
Декартово
произведение отрезка![]() на
отрезок
на
отрезок ![]() ….является
прямоугольником с вершинами
….является
прямоугольником с вершинами ![]()
Решение: Декартовым произведением отрезка на отрезок является прямоугольник с вершинами
Тема: Элементы комбинаторики На 10 карточках написаны буквы так, что из этих карточек можно получить слово ИСЧИСЛЕНИЕ. Сколько существует различных 10-буквенных слов, которые можно образовать с помощью этих десяти карточек?
|
151200 | |
Решение:
Разобьем
карточки на группы. Первая группа
содержит букву И. Элементы ее неразличимы.
Число элементов первой группы ![]() .
Вторую группу образуют карточки с буквой
С. Число элементов второй группы
.
Вторую группу образуют карточки с буквой
С. Число элементов второй группы ![]() .
Третью группу образуют карточки с буквой
Ч. Число элементов этой группы
.
Третью группу образуют карточки с буквой
Ч. Число элементов этой группы ![]() .
Четвертую группу образуют карточки с
буквой Л, число элементов
.
Четвертую группу образуют карточки с
буквой Л, число элементов ![]() .
Пятую группу образуют карточки с буквой
Е. Число элементов
.
Пятую группу образуют карточки с буквой
Е. Число элементов ![]() .
Шестая группа состоит из карточек с
буквой Н. Количество элементов этой
группы
.
Шестая группа состоит из карточек с
буквой Н. Количество элементов этой
группы ![]() .
Число различных 10-буквенных слов,
образованных этими 10 карточками,
совпадает с числом различных перестановок
с повторениями и равно
.
Число различных 10-буквенных слов,
образованных этими 10 карточками,
совпадает с числом различных перестановок
с повторениями и равно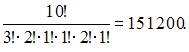
Тема: Неориентированные графы Из представленных графов полным является граф …
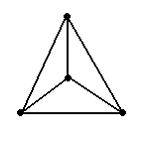
Решение: Полным называют граф без петель и кратных ребер, в котором любые две вершины соединены ребром.
Тема:
Операции над высказываниями
Из
трех логических выражений:
эквивалентными
являются …![]() и
и ![]()
Решение:
Составим
таблицы истинности для ![]()

 Сопоставляя
таблицы, видим, что
Сопоставляя
таблицы, видим, что ![]() не
эквивалентна формулам
не
эквивалентна формулам ![]() и
и ![]() ,
а
и
эквивалентны.
,
а
и
эквивалентны.
Тема:
Декартово произведение множеств
Декартово
произведение ![]() множеств
множеств ![]() и
и ![]() равно
…
равно
…![]()
Тема: Декартово произведение множеств Декартово произведение множеств и представляет собой …
|
|
|
окружность , лежащую в плоскости |
Тема:
Неориентированные графы
Для
графа, изображенного на рисунке,
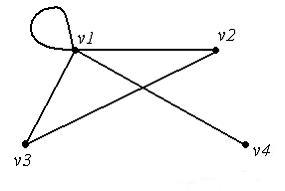 степень
вершины
степень
вершины ![]() равна
…
равна
…
|
|
|
5 |
|
|
|
4 |
|
|
|
3 |
|
|
|
1 |
Решение:
Степенью
вершины называют удвоенное количество
петель, инцидентных этой вершине, плюс
количество остальных инцидентных ей
ребер. То есть степень вершины![]() равна
пяти.
равна
пяти.
Тема: Элементы комбинаторики На школьном вечере присутствуют 5 девушек и 6 юношей. Выбрать из них 2 пары для танца можно ___ способом(-ами).
|
300 | |
Решение:
Сначала
в произвольном порядке выбираем двух
юношей из шести ![]() способами
(сочетания 2 из 6), затем выбираем для них
девушек, причем теперь порядок выбора
важен. Число способов выбрать двух
девушек из пяти равно
способами
(сочетания 2 из 6), затем выбираем для них
девушек, причем теперь порядок выбора
важен. Число способов выбрать двух
девушек из пяти равно ![]() (размещения
2 из 5).
Тогда число способов для выбора
двух пар по правилу произведения равно:
(размещения
2 из 5).
Тогда число способов для выбора
двух пар по правилу произведения равно:
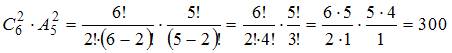
Тема: Операции над высказываниями На вопрос, кто из трех учащихся изучал логику, был получен правильный ответ: если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй. Тогда логику …
|
|
|
изучал третий учащийся |
|
|
|
изучал второй учащийся |
|
|
|
изучал первый учащийся |
|
|
|
никто из учащихся не изучал |
Решение:
Обозначим
через a, b, c высказывания,
состоящие соответственно в том, что
первый, второй, третий учащиеся изучали
логику. Запишем условие задачи с
помощью a, b, cи
логических операций. Получим выражение ![]() .
Известно, что это высказывание истинно.
Составим таблицу истинности полученного
выражения:
.
Известно, что это высказывание истинно.
Составим таблицу истинности полученного
выражения:
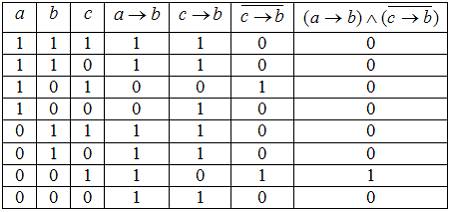 Только
в предпоследней строке получившееся
выражение принимает истинное значение,
а все остальные значения ложны. При этом
высказывания a и b ложны,
а c –
истинно. Значит, логику изучал только
третий учащийся.
Только
в предпоследней строке получившееся
выражение принимает истинное значение,
а все остальные значения ложны. При этом
высказывания a и b ложны,
а c –
истинно. Значит, логику изучал только
третий учащийся.
Тема:
Операции над высказываниями
Высказывание
«![]() »
означает, что …
»
означает, что …
|
|
|
« – любое число» |
|
|
|
«
принадлежит
интервалу |
|
|
|
«
принадлежит
промежутку |
|
|
|
« не существует» |
Решение:
Высказывание
«
»
– это дизъюнкция двух неравенств, и
решением является объединение
промежутков: ![]() .
То есть
–
любое число.
.
То есть
–
любое число.
Тема:
Декартово произведение множеств
Даны
множества
,
и
.
Тогда число элементов декартова
произведения множеств ![]() равно…
равно…
|
|
|
24 |
|
|
|
10 |
|
|
|
2 |
|
|
|
12 |
Решение:
Декартово
произведение множеств – это множество,
состоящее из упорядоченных пар элементов,
первым элементом которых являются
элементы первого множества, вторым –
элементы второго, то есть ![]() Множество,
состоящее из шести элементов, умножается
на множество из четырех элементов, тогда
по свойству декартова произведения
получается множество, состоящее из 24
элементов.
Множество,
состоящее из шести элементов, умножается
на множество из четырех элементов, тогда
по свойству декартова произведения
получается множество, состоящее из 24
элементов.
Тема:
Неориентированные графы
Для
графа, изображенного на рисунке,
 гамильтоновым
циклом является маршрут …
гамильтоновым
циклом является маршрут …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Цикл называется гамильтоновым, если он простой и содержит все вершины графа. Для данного графа гамильтоновым циклом служит, например, маршрут
Тема: Неориентированные графы Матрица смежности графа, изображенного на рисунке имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Матрицей
смежности графа называют квадратную
матрицу
размера
,
строкам и столбцам которой соответствуют
вершины помеченного графа (первый
столбец (строка) отвечает первой вершине
и т.д.), а ее элементы ![]() равны
количеству ребер, инцидентных вершинам
с номерами i и j.
Согласно определению составляем матрицу
смежности
равны
количеству ребер, инцидентных вершинам
с номерами i и j.
Согласно определению составляем матрицу
смежности
Тема: Декартово произведение множеств Даны множества , и . Тогда число элементов декартова произведения множеств равно…
|
|
|
24 |
|
|
|
10 |
|
|
|
2 |
|
|
|
12 |
Решение: Декартово произведение множеств – это множество, состоящее из упорядоченных пар элементов, первым элементом которых являются элементы первого множества, вторым – элементы второго, то есть Множество, состоящее из шести элементов, умножается на множество из четырех элементов, тогда по свойству декартова произведения получается множество, состоящее из 24 элементов.
Тема: Элементы комбинаторики Сколько чисел меньших, чем миллион можно написать с помощью цифр 3 и 7?
|
126 | |
Решение:
С
помощью двух различных цифр можно
записать ![]() –
шестизначных чисел,
–
пятизначных чисел,
–
шестизначных чисел,
–
пятизначных чисел, ![]() –
четырехзначных чисел,
–
четырехзначных чисел, ![]() –
трехзначных чисел,
–
трехзначных чисел, ![]() –
двузначных чисел,
–
двузначных чисел, ![]() –
однозначных чисел. Просуммируем эти
композиции
.
–
однозначных чисел. Просуммируем эти
композиции
.
Тема:
Операции над высказываниями
Формулой,
равносильной формуле ![]() ,
является …
,
является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
![]()
Тема: Операции над высказываниями Таблица истинности для формулы представляет собой …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
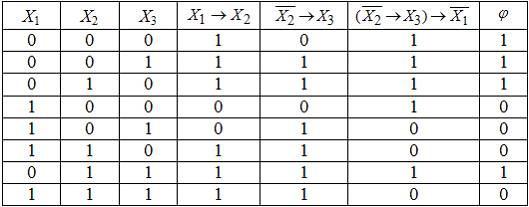
Тема: Неориентированные графы Эйлеровым является граф …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Эйлеровым называют граф содержащий эйлеров цикл. Цикл называется эйлеровым, если он простой и содержит все ребра графа. Критерий эйлеровости графа: граф называется Эйлеровым тогда и только тогда, когда степени всех его вершин четные. Из представленных графов только граф имеет четные степени всех вершин.
Тема: Операции над высказываниями Высказывание « » означает, что …
|
|
|
« – любое число» |
|
|
|
« принадлежит интервалу » |
|
|
|
« принадлежит промежутку » |
|
|
|
« не существует» |
Решение: Высказывание « » – это дизъюнкция двух неравенств, и решением является объединение промежутков: . То есть – любое число.
Тема: Элементы комбинаторики В урне находятся 10 белых, 15 красных, 20 голубых шаров. Все шары пронумерованы. Сколькими различными способами можно взять из урны три шара разных цветов?
|
3000 | |
Решение: Возьмем один белый шар. Это действие можно выполнить 10 способами (по числу различных белых шаров в урне). К выбранному белому шару присоединим красный шар, который можно взять 15 различными способами (по числу различных красных шаров в урне). К выбранной присоединим голубой шар, который можно взять 20 способами (по числу различных голубых шаров в урне). Таким образом, можно образовать различные тройки разноцветных шаров. Число различных способов выбора троек разноцветных шаров совпадает с числом различных трех действий и по правилу умножения равно:
Тема:
Неориентированные графы
Для
графа G, изображенного на рисунке,
 матрица
смежности имеет вид …
матрица
смежности имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Операции над высказываниями Отрицанием высказывания «Если я сдам зачет, то пойду в кафе с друзьями или на вечеринку» является высказывание:
|
|
|
«Я сдам зачет и не пойду ни в кафе с друзьями, ни на вечеринку» |
|
|
|
«Если я не сдам зачет, то не пойду в кафе с друзьями или не пойду на вечеринку» |
|
|
|
«Если я не сдам зачет, то, несмотря ни на что, пойду в кафе с друзьями или на вечеринку» |
|
|
|
«Я не сдам зачет и не пойду ни в кафе с друзьями, ни на вечеринку» |
Решение:
Введем
простые высказывания: A –
«я сдам зачет», B –
«пойду в кафе с друзьями», C–
«пойду на вечеринку».
Тогда высказывание
«Если я сдам зачет, то пойду в кафе с
друзьями или на вечеринку» имеет
вид ![]() .
Отрицание
этого высказывания
.
Отрицание
этого высказывания ![]() .
Получаем
высказывание: «Я сдам зачет и не пойду
ни в кафе с друзьями, ни на вечеринку».
.
Получаем
высказывание: «Я сдам зачет и не пойду
ни в кафе с друзьями, ни на вечеринку».
Тема: Элементы комбинаторики Из колоды в 36 карт наудачу без возвращения вынимают по одной карте 3 раза. Сколько существует различных способов получения трех карт, среди которых на первых двух местах – бубны, а на третьем – пики.
|
648 | |
Решение:
В
колоде 9 бубен и 9 пик. Получение тройки
карт «бубны, бубны, пики» можно
рассматривать как результат двух
действий. Первое действие – получение
на первых картах «бубны, бубны». Поскольку
порядок карт существенен, то число
различных способов осуществления
первого действия совпадает с числом
размещений из 9 элементов по 2: ![]() .
Второе
действие – взятие «пики» на третьем
месте. Число способов выполнить второе
действие равно 9 (по количеству «пик»).
По правилу умножения, получим:
.
Второе
действие – взятие «пики» на третьем
месте. Число способов выполнить второе
действие равно 9 (по количеству «пик»).
По правилу умножения, получим: ![]() .
.
Тема: Декартово произведение множеств Декартово произведение отрезка на отрезок …
|
|
|
является прямоугольником с вершинами |
|
|
|
является
отрезком |
|
|
|
равно 2 |
|
|
|
равно 13 |
Решение:
Декартовым
произведением отрезка ![]() на
отрезок
на
отрезок ![]() является
прямоугольник с вершинами
является
прямоугольник с вершинами
Тема:
Неориентированные графы
Матрица
инцидентности графа, изображенного на
рисунке
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы комбинаторики В урне находятся 5 белых, 7 красных, 6 голубых шаров. Сколько существует способов извлечь 9 шаров так, чтобы среди них оказалось 2 белых, 3 красных и 4 голубых шара?
|
5250 | |
Решение:
Всего
в урне 18 шаров. Сначала выберем два белых
шара из 5 белых шаров. Это действие можно
выполнить ![]() способами.
Второе действие состоит в выборе трех
красных шаров из 7 красных шаров. Это
действие можно выполнить
способами.
Второе действие состоит в выборе трех
красных шаров из 7 красных шаров. Это
действие можно выполнить ![]() способами.
Третье действие состоит в выборе четырех
голубых шаров. Оно может быть
выполнено
способами.
Третье действие состоит в выборе четырех
голубых шаров. Оно может быть
выполнено![]() способами.
По
правилу умножения получим:
способами.
По
правилу умножения получим: ![]()