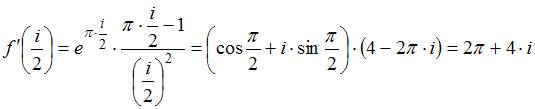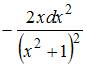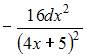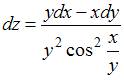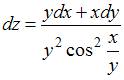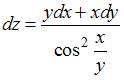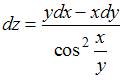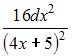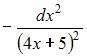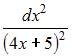1) Тема: Дифференциальная геометрия поверхностей
Уравнение касательной плоскости к прямому геликоиду в точке имеет вид …
![]()
![]()
![]()
![]()
2) Тема: Дифференциальная геометрия кривых
Длина дуги кривой при равна
Решение:
Длина дуги кривой вычисляется по формуле где дифференциал дуги. Вычислив получаем .
3) Тема: Основные понятия топологии
Внешностью множества в топологическом пространстве с топологией является пустое множество
Решение: Внешность M – это совокупность всех внутренних точек дополнения к множеству M, то есть входящих в дополнение к M с какой-либо своей окрестностью (открытым множеством). Дополнением является множество – закрытое множество, которое не содержит в себе ни одного открытого множества из данной топологии. Таким образом, внешностью множества в данном случае будет пустое множество.
4) Тема: Асимптоты кривой
Асимптоты
кривой 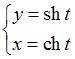 имеют
вид
имеют
вид ![]() и
и ![]()
Тема:
Дифференциальная геометрия
поверхностей
Уравнение
касательной плоскости к эллиптическому
параболоиду ![]() в
точке
в
точке ![]() имеет
вид …
имеет
вид …
|
|
|
|
Решение:
Для
функции вида ![]() уравнение
касательной плоскости имеет вид
уравнение
касательной плоскости имеет вид![]() Найдем
частные производные функции
Найдем
частные производные функции 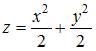 :
:![]() Тогда
уравнение касательной плоскости примет
вид:
Тогда
уравнение касательной плоскости примет
вид: ![]() Получим
Получим ![]()
Тема:
Дифференциальная геометрия кривых
Траектория
движущейся точки задается уравнением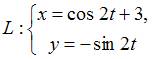 Тогда
значение нормального ускорения в
момент
Тогда
значение нормального ускорения в
момент![]() равно
…
равно
…![]()
Решение:
Нормальное
ускорение на параметрически заданной
кривой вычисляется как 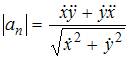 Вычислим
производные первого и второго
порядка.
Найдём
Вычислим
производные первого и второго
порядка.
Найдём 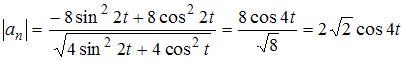 Тогда
при
Тогда
при
![]()
Тема:
Основные понятия топологии
Внешностью
множества ![]() в
топологическом пространстве
с
топологией
является
…
в
топологическом пространстве
с
топологией
является
…
Решение: Внешность – это совокупность всех внутренних точек дополнения к множеству , то есть входящих в дополнение к с какой-либо своей окрестностью (открытым множеством). Таким образом, внешностью множества в данном случае будет
Тема:
Асимптоты кривой
Уравнение
асимптоты кривой, заданной в полярной
системе координат 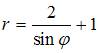 ,
имеет вид …
,
имеет вид …
Решение:
Из
условия существования асимптоты
кривой ![]() получаем
что
получаем
что ![]() .
Так как
.
Так как 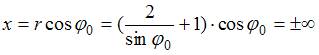 ,
, 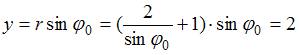 то
уравнение асимптоты имеет вид:
то
уравнение асимптоты имеет вид: ![]()
Тема:
Дифференциальная геометрия кривых
Уравнение
касательной к циклоиде 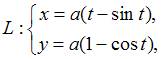 в
точке
в
точке ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
В
точке
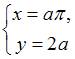 .
Найдем производные:
.
Найдем производные: 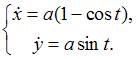 Тогда
Тогда 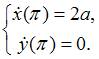 Подставляя
полученные данные в уравнение
касательной
Подставляя
полученные данные в уравнение
касательной 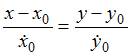 ,
получим
,
получим![]() или
или ![]()
Тема:
Дифференциальная геометрия
поверхностей
Вектор
нормали
к
поверхности гиперболического
параболоида 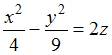 в
точке
в
точке ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Координаты
вектора нормали
в
точке ![]() к
поверхности, заданной явно в виде
,
вычисляются по формуле
к
поверхности, заданной явно в виде
,
вычисляются по формуле ![]() .
Вычислим частные производные функции
.
Вычислим частные производные функции 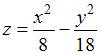 в
точке
:
в
точке
: 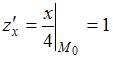 ;
; 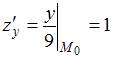 .
Тогда
вектор нормали в точке
будет
равен:
.
Тогда
вектор нормали в точке
будет
равен: ![]()
Тема:
Дифференциальная геометрия
кривых
Кривая ![]() задана
в полярных координатах:
задана
в полярных координатах: ![]() .
Тогда длина дуги при
.
Тогда длина дуги при ![]() ,
равна …
,
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как дифференциал дуги ![]() ,
то длина дуги вычисляется как:
,
то длина дуги вычисляется как:
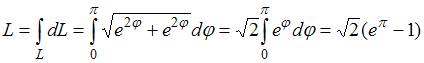
Тема: Асимптоты кривой Асимптоты графика кривой , заданной в полярных координатах, имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Из
условия существования асимптоты
кривой
получаем
что ![]()
![]() .Так
как
.Так
как ![]() ,
,![]() и
и 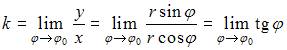 ,
, 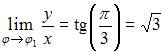 ,
, 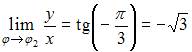 ,
, 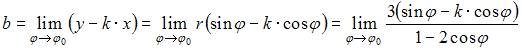 .
.
То
есть 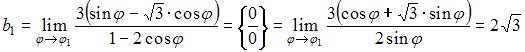
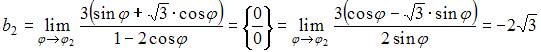 Тогда
график имеет две асимптоты:
Тогда
график имеет две асимптоты: ![]()
![]()
Тема: Дифференциальная геометрия кривых Уравнение нормали к кривой в точке имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Представим
неявно заданную кривую в виде функции ![]() .
Так
как уравнение нормали кривой, заданной
неявно, имеет вид
.
Так
как уравнение нормали кривой, заданной
неявно, имеет вид 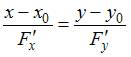 ,
вычислим частные производные
функции
,
вычислим частные производные
функции ![]() :
:
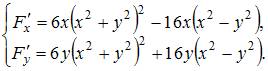 Их
значения в точке
равны:
Их
значения в точке
равны:
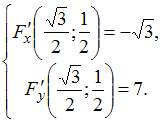 Тогда,
подставляя полученные данные в уравнение
нормали, получим
Тогда,
подставляя полученные данные в уравнение
нормали, получим
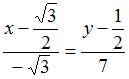 или
или
Тема:
Асимптоты кривой
Кривая
на плоскости задана уравнениями в
параметрической форме:
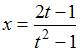 ,
, 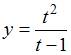 .
Тогда
количество асимптот кривой равно …
.
Тогда
количество асимптот кривой равно …
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
|
|
|
3 |
Решение:
Из
условия существования горизонтальных
асимптот:
![]() ,
, ![]() ,
и
,
и ![]() ,
, ![]() ,
следует, что
–
горизонтальная асимптота.
Из условия
существования вертикальных
асимптот:
,
следует, что
–
горизонтальная асимптота.
Из условия
существования вертикальных
асимптот: ![]() ,
, ![]() следует,
что, так как нет таких
следует,
что, так как нет таких ![]() ,
то вертикальные асимптоты отсутствуют.
Из
условия существования наклонных асимптот
имеем:
,
то вертикальные асимптоты отсутствуют.
Из
условия существования наклонных асимптот
имеем:
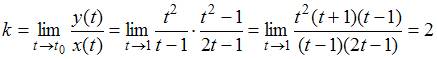 ,
,
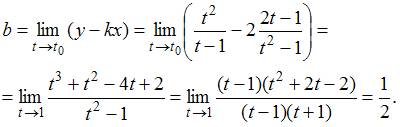 То
есть
То
есть ![]() –
наклонная асимптота. Всего асимптот
две.
–
наклонная асимптота. Всего асимптот
две.
Тема:
Дифференциальная геометрия
поверхностей
Первая
квадратичная форма поверхности ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Параметризуем
сферу
:
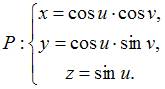 Запишем
ее в виде вектор-функции
Запишем
ее в виде вектор-функции ![]() и
вычислим ее частные производные:
и
вычислим ее частные производные: ![]() ;
; ![]() .
Коэффициенты
первой квадратичной формы
определим
по формулам
;
;
.
Тогда
.
Коэффициенты
первой квадратичной формы
определим
по формулам
;
;
.
Тогда
![]() ;
;
![]() ;
;
![]() .
Таким
образом,
.
Таким
образом,
Тема: Дифференциальная геометрия кривых Траектория движущейся точки задается уравнением Тогда значение касательного ускорения в момент равно …
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение: Касательное ускорение на параметрически заданной кривой вычисляется как . Вычислим производные первого и второго порядка. Найдем , при любых значениях .
Тема: Асимптоты кривой Асимптоты кривой имеют вид …
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
и |
Решение: Кривая описывается соотношением , то есть функция представлена в явном виде. В точке функция имеет разрыв, поэтому уравнение вертикальной асимптоты имеет вид: . Наклонные или горизонтальные асимптоты определяются уравнением (для горизонтальных асимптот ). 1. Находим асимптоту при (правую асимптоту): , . Следовательно, уравнение правой асимптоты имеет вид: . 2. Аналогично находим асимптоту при (левую асимптоту): , . Следовательно, уравнение левой асимптоты совпадает с уравнением правой асимптоты и имеет вид: . Таким образом, прямые и являются асимптотами заданной кривой.
Тема:
Дифференциальная геометрия
поверхностей
Точка
с координатами ![]() на
поверхности
на
поверхности ![]() является
…
является
…
|
|
|
гиперболической точкой |
|
|
|
параболической точкой |
|
|
|
эллиптической точкой |
|
|
|
точкой уплощения |
Решение:
Тип
точки на поверхности определяется по
виду соприкасающегося параболоида в
этой точке к поверхности.
Построим
соприкасающийся параболоид:
.
Вычислим
частные производные второго
порядка:
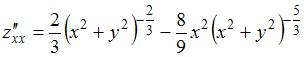 ;
; 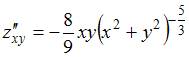 ;
; 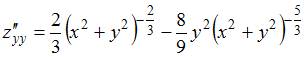 .
В
точке
.
В
точке
![]() ;
; ![]() ;
; ![]() .
Тогда
соприкасающийся параболоид
.
Тогда
соприкасающийся параболоид 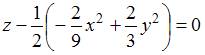 ,
или
,
или ![]() является
гиперболическим параболоидом, а сама
точка
относится
к гиперболическому типу.
является
гиперболическим параболоидом, а сама
точка
относится
к гиперболическому типу.
Тема:
Дифференциальная геометрия
поверхностей
Огибающая
семейства сфер ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Из
системы 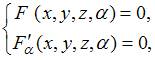 следует,
что
следует,
что
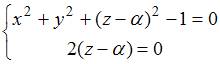 ,
, 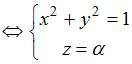 .
Таким
образом, огибающая имеет вид
.
Это цилиндр.
.
Таким
образом, огибающая имеет вид
.
Это цилиндр.
Тема: Основные понятия топологии Гомеоморфной к тору является …
|
|
|
«кружка с ручкой» |
|
|
|
сфера |
|
|
|
«крендель» |
|
|
|
куб |
Решение: Тор является многосвязным, а сфера и куб являются односвязными. Род тора равен 1, а род «кренделя» 2. Только с поверхностью «кружки с ручкой» можно установить взаимно-однозначное соответствие, поэтому поверхностью гомеоморфной к тору является поверхность «кружки с ручкой».
Тема: Дифференциальная геометрия поверхностей Точка с координатами на поверхности является …
|
|
|
гиперболической точкой |
|
|
|
параболической точкой |
|
|
|
эллиптической точкой |
|
|
|
точкой уплощения |
Решение: Тип точки на поверхности определяется по виду соприкасающегося параболоида в этой точке к поверхности. Построим соприкасающийся параболоид: . Вычислим частные производные второго порядка: ; ; . В точке ; ; . Тогда соприкасающийся параболоид является гиперболическим параболоидом, а сама точка относится к гиперболическому типу.
Тема: Основные понятия топологии Тривиальная топологическая структура на множестве задается множеством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Множество подмножеств данного множества задает топологию, если выполняются следующие свойства: – пустое множество и данное множество входят в ; – объединение любого числа и пересечение конечного числа подмножеств из снова принадлежит . А тривиальная топологическая структура состоит из пустого множества и самого множества , то есть верным будет ответ: .
Тема:
Асимптоты кривой
Асимптоты
кривой ![]() имеют
вид …
имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Дифференциальная геометрия кривых
К
кривой ![]() проведена
нормаль, параллельная прямой
проведена
нормаль, параллельная прямой ![]() .
Тогда уравнение нормали имеет вид …
.
Тогда уравнение нормали имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Угловой
коэффициент прямой ![]() .
Так как касательная перпендикулярна
нормали, точку касания
.
Так как касательная перпендикулярна
нормали, точку касания ![]() найдем
из условия
найдем
из условия ![]() ,
или
,
или 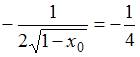 .
Решив это уравнение, получим
.
Решив это уравнение, получим ![]() ,
, ![]() .
Тогда
уравнение нормали примет вид:
.
Тогда
уравнение нормали примет вид: ![]() или
или
Тема:
Асимптоты кривой
Асимптоты
графика функции ![]() задаются
уравнениями …
задаются
уравнениями …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
Решение:
Функция
представлена в явном виде
.
В
точке
функция
имеет разрыв, поэтому уравнение
вертикальной асимптоты имеет
вид
.
Наклонные
или горизонтальные асимптоты определяются
уравнением ![]() (для
горизонтальных асимптот
).
1.
Находим асимптоту
(для
горизонтальных асимптот
).
1.
Находим асимптоту ![]() при
(правую
асимптоту):
при
(правую
асимптоту):
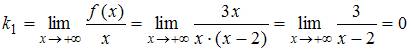 ,
,
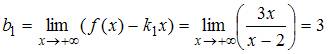 .
Следовательно,
уравнение правой асимптоты имеет
вид
.
2.
Аналогично находим асимптоту
при
(левую
асимптоту):
.
Следовательно,
уравнение правой асимптоты имеет
вид
.
2.
Аналогично находим асимптоту
при
(левую
асимптоту):
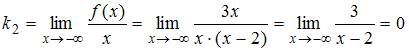 ;
;
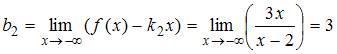 .
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптотой и имеет
вид
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
.
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптотой и имеет
вид
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
Тема: Основные понятия топологии Тривиальная топологическая структура на множестве задается множеством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Множество подмножеств данного множества задает топологию, если выполняются следующие свойства: – пустое множество и данное множество входят в ; – объединение любого числа и пересечение конечного числа подмножеств из снова принадлежит . А тривиальная топологическая структура состоит из пустого множества и самого множества , то есть верным будет ответ: .
Тема: Дифференциальная геометрия поверхностей Первая квадратичная форма поверхности имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференциальная геометрия кривых Траектория движущейся точки задается уравнением Тогда значение касательного ускорения в момент равно …
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение: Касательное ускорение на параметрически заданной кривой вычисляется как . Вычислим производные первого и второго порядка. Найдем , при любых значениях .
Тема: Дифференциальная геометрия поверхностей Вектор нормали к поверхности гиперболического параболоида в точке имеет координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Координаты вектора нормали в точке к поверхности, заданной явно в виде , вычисляются по формуле . Вычислим частные производные функции в точке : ; . Тогда вектор нормали в точке будет равен:
Тема: Асимптоты кривой Асимптоты кривой имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
кривой, заданной неявно многочленом
-
ой степени уравнения асимптот задаются
соотношением: ![]() ,
где
,
где ![]() -
совокупность членов степени
,
а
и
-
совокупность членов степени
,
а
и ![]() находятся
из уравнения
находятся
из уравнения ![]() .
Составив
уравнение
.
Составив
уравнение ![]() ,
получим зависимость между
и
:
,
получим зависимость между
и
: ![]() .
Так
как
.
Так
как ![]() ;
; ![]() ;
; ![]() ,
то
уравнение асимптоты примет вид:
,
то
уравнение асимптоты примет вид: ![]() и
и
ДЕ4. Дифференциальное и интегральное исчисление
Тема:
Дифференциалы и теоремы о дифференцируемых
функциях
Дифференциал
функции![]() равен
равен ![]()
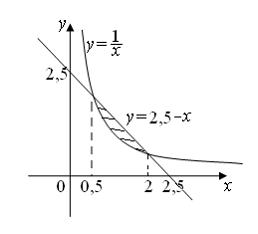
Тема: Приложения определенного интеграла Площадь фигуры, изображенной на рисунке
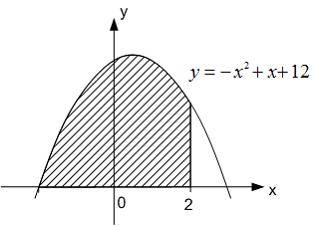
Равна ![]()
Решение:
Площадь
данной фигуры можно вычислить по
формуле 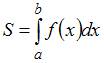 ,
где а-«левая» точка пересечения параболы
и оси Ох,
,
где а-«левая» точка пересечения параболы
и оси Ох, ![]() ,
а
,
а ![]() .
Определим точки пересечения параболы
и оси
.
Определим точки пересечения параболы
и оси ![]() ,
решив уравнение
,
решив уравнение ![]() .Получаем:
.Получаем: ![]() .
.
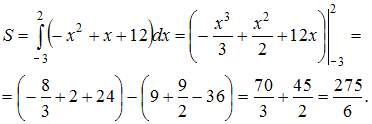
Тема:
Непрерывность функции, точки
разрыва
Количество
точек разрыва функции 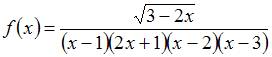 равно
2.
равно
2.
Решение:
Точку
называют
точкой разрыва функции
,
если она не является непрерывной в этой
точке. В частности, точками разрыва
данной функции могут являться точки, в
которых знаменатель равен нулю, то
есть ![]()
![]()
![]()
![]() .
Однако область определения
функции
.
Однако область определения
функции ![]() определяется
как
определяется
как ![]() ,
то есть имеет вид
,
то есть имеет вид![]() .
Тогда
имеет
2 точки разрыва.
,
удовлетворяющие условию
.
.
Тогда
имеет
2 точки разрыва.
,
удовлетворяющие условию
.
Тема:
Дифференциальное исчисление ФНП
Частная
производная![]() функции
функции ![]() имеет
вид
имеет
вид ![]() .
.
Тема:
Непрерывность функции, точки
разрыва
Точка
является
точкой разрыва функции …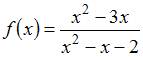
Решение:
Точку
называют
точкой разрыва функции
,
если она не является непрерывной в этой
точке. В частности, точками разрыва
данных функций являются точки, в которых
знаменатель равен нулю, то есть ![]() ,
или:
,
или: ![]()
![]() .
Точка
.
Точка
не
является точкой разрыва функции 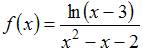 ,
так как область определения функции
,
так как область определения функции ![]() имеет
вид
имеет
вид ![]() ,и
,и![]() ;
;
не
является точкой разрыва функции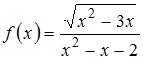 ,
так как область определения функции
,
так как область определения функции ![]() имеет
вид
имеет
вид ![]() ,
и
,
и ![]() ;
;
не
является точкой разрыва функции 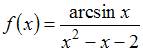 ,
так как область определения функции
,
так как область определения функции ![]() имеет
вид
имеет
вид ![]() ,
и
,
и ![]() .
.
Таким образом, точка является точкой разрыва функции .
Тема: Дифференциальное исчисление ФНП Смешанная частная производная второго порядка функции имеет вид …
Тема:
Приложения определенного интеграла
Площадь
фигуры, ограниченной параболой ![]() и
осью
,
равна …
и
осью
,
равна …
|
|
|
36 |
Решение:
Площадь
данной фигуры можно вычислить по
формуле
где
и ![]() –
это точки пересечения параболы и оси
,
а
–
это точки пересечения параболы и оси
,
а ![]() .
Определим точки пересечения параболы
и оси
,
решив уравнение
.
Определим точки пересечения параболы
и оси
,
решив уравнение ![]() .
Получаем:
.
Получаем: ![]() и
и ![]() .
Тогда
.
Тогда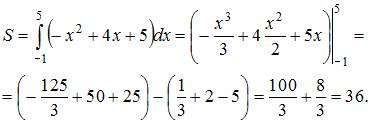
Тема:
Дифференциалы и теоремы о дифференцируемых
функциях
Дифференциал
второго порядка функции ![]() равен
…
равен
…
|
|
|
|
Решение:
Дифференциал
второго порядка ![]() функции
выражается
формулой
функции
выражается
формулой ![]() .Тогда
вычислив
.Тогда
вычислив 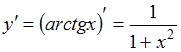 и
и 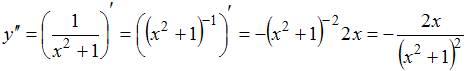 получаем
получаем 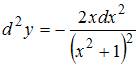 .
.
Тема: Дифференциальное исчисление ФНП Частная производная функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
вычислении частной производной
по
переменной
,
переменные
и ![]() рассматриваем
как постоянные величины. Тогда
рассматриваем
как постоянные величины. Тогда
![]() .
.
Тема: Непрерывность функции, точки разрыва Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Решение: Вычислим односторонние пределы функции в точке : , . Так как один из односторонних пределов в точке , а именно , то точка является точкой разрыва второго рода.
Тема:
Дифференциалы и теоремы о дифференцируемых
функциях
Дифференциал
функции ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Дифференциал ![]() функции
выражается
формулой
функции
выражается
формулой ![]() .
Тогда
вычислив
.
Тогда
вычислив 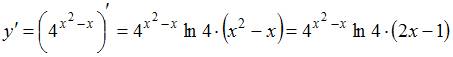 ,
получаем
,
получаем ![]() .
.
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
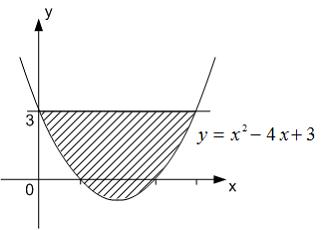 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Площадь
данной фигуры можно вычислить по
формуле 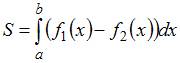 ,
где
,
где ![]() ,
, ![]() ,
, ![]() ,
–
«правая» точка пересечения параболы
и
прямой
.
Определим значение
,
решив уравнение
,
–
«правая» точка пересечения параболы
и
прямой
.
Определим значение
,
решив уравнение ![]() .
Получаем:
.
Получаем: ![]() .
Тогда
.
Тогда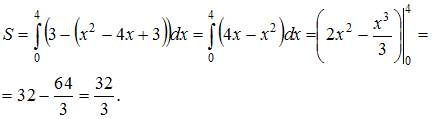
Тема:
Непрерывность функции, точки разрыва
Точка
разрыва функции 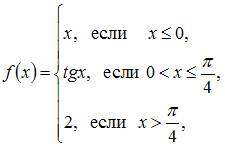 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Данная
функция определена и непрерывна на
каждом из интервалов 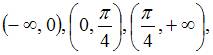 и
меняет свое аналитическое выражение в
точках
и
меняет свое аналитическое выражение в
точках ![]() и
и ![]() .
Поэтому функция может иметь разрыв
только в этих точках. Исследуем их на
непрерывность.
Для точки
.
Поэтому функция может иметь разрыв
только в этих точках. Исследуем их на
непрерывность.
Для точки ![]() вычислим
односторонние пределы и значение функции
в этой точке:
вычислим
односторонние пределы и значение функции
в этой точке:
![]() ,
,
![]() ,
и
,
и ![]() .
Так
как
.
Так
как ![]() ,
то точка
является
точкой непрерывности данной функции.
Для
точки
,
то точка
является
точкой непрерывности данной функции.
Для
точки ![]() вычислим
односторонние пределы и значение функции
в этой точке:
вычислим
односторонние пределы и значение функции
в этой точке:
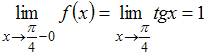 ,
,
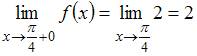 ,
и
,
и 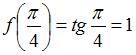 .
Так
как
.
Так
как 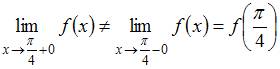 ,
то точка
является
точкой разрыва первого рода.
,
то точка
является
точкой разрыва первого рода.
Тема: Дифференциальное исчисление ФНП Смешанная частная производная второго порядка функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: При вычислении частной производной функции по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
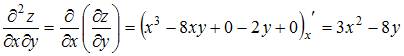
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное
значение функции ![]() при
при ![]() ,
вычисленное с использованием дифференциала
первого порядка, равно …
,
вычисленное с использованием дифференциала
первого порядка, равно …
|
|
|
|
Тема:
Дифференциальное исчисление ФНП
Значение
частной производной
функции 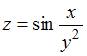 в
точке
в
точке 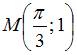 равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
вычислении частной производной
по
переменной
переменную
рассматриваем
как постоянную величину.
Тогда
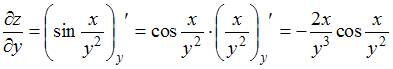 .
Следовательно,
.
Следовательно, 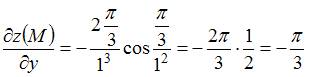
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
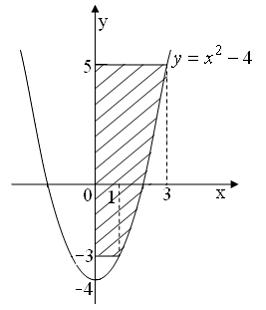 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
Решение:
Площадь
данной фигуры можно вычислить по
формуле 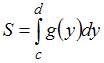 ,
где
,
где ![]()
![]()
![]() .
Тогда
.
Тогда 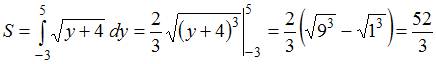
Тема: Непрерывность функции, точки разрыва Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Решение: Вычислим односторонние пределы функции в точке : , . Так как один из односторонних пределов в точке , а именно , то точка является точкой разрыва второго рода.
Тема:
Дифференциалы и теоремы о дифференцируемых
функциях
Дифференциал
второго порядка функции ![]() равен
…
равен
…
|
|
|
|
Тема: Дифференциальное исчисление ФНП Частная производная второго порядка функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: При вычислении частной производной функции по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда .
Тема: Непрерывность функции, точки разрыва Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Решение: Вычислим односторонние пределы функции в точке : , . Так как один из односторонних пределов в точке , а именно , то точка является точкой разрыва второго рода.
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
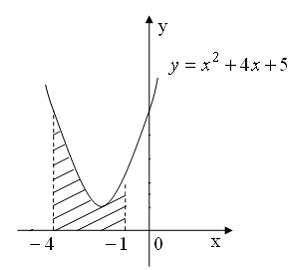 равна
…
равна
…
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
|
|
|
Решение:
Площадь
данной фигуры можно вычислить по
формуле
,
где ![]() ,
, ![]() ,
а
,
а ![]() .
Тогда
.
Тогда
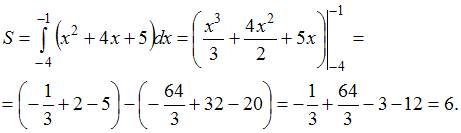
Тема:
Дифференциалы и теоремы о дифференцируемых
функциях
Дана
функция ![]() .
Тогда больший действительный корень
производной этой функции принадлежит
промежутку …
.
Тогда больший действительный корень
производной этой функции принадлежит
промежутку …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Эта
функция представляет собой полином
пятого порядка и дифференцируема на
всей числовой оси. Согласно теореме
Ролля между двумя корнями (нулями) этой
функции находится по крайней мере один
корень ее производной. Поскольку
представляет
собой полином (4-го порядка), то между
двумя корнями функции
находится
ровно один корень ее производной
.
Найдем
корни функции
: ![]() .
Тогда больший действительный корень
функции
принадлежит
интервалу
.
Тогда больший действительный корень
функции
принадлежит
интервалу
Тема: Дифференциальное исчисление ФНП Частная производная функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференциалы и теоремы о дифференцируемых функциях Дана функция . Тогда меньший действительный корень производной этой функции принадлежит промежутку …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Эта функция представляет собой полином 6-го порядка и дифференцируема на всей числовой оси. Согласно теореме Ролля между двумя корнями (нулями) этой функции находится по крайней мере один корень ее производной. Поскольку представляет собой полином (5-го порядка), то между двумя корнями функции находится ровно один корень ее производной . Найдем корни функции : . Тогда меньший действительный корень функции принадлежит интервалу .
Тема:
Непрерывность функции, точки разрыва
Точка
разрыва функции 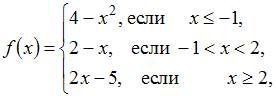 равна
…2
равна
…2
Тема: Приложения определенного интеграла Площадь фигуры, ограниченной параболой и осью , равна …
|
|
|
36 |
|
|
|
38 |
|
|
|
|
|
|
|
|
Решение: Площадь данной фигуры можно вычислить по формуле , где и – это точки пересечения параболы и оси , а . Определим точки пересечения параболы и оси , решив уравнение . Получаем: и . Тогда
Тема:
Дифференциальное исчисление ФНП
Полный
дифференциал функции 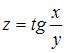 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Полный
дифференциал функции нескольких
переменных равен сумме произведений
частных производных этой функции на
дифференциалы соответствующих независимых
переменных, то есть
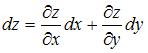 .
Тогда
.
Тогда
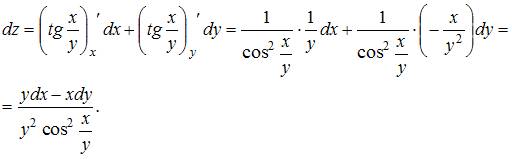
Тема: Дифференциалы и теоремы о дифференцируемых функциях Предел равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
вычисления данного предела применим
правило Лопиталя. Так как ![]() ,
то при помощи алгебраических преобразований
получим неопределенность вида
,
то при помощи алгебраических преобразований
получим неопределенность вида ![]() ,
или
,
или ![]() ,
например:
,
например:
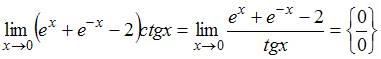 .
Тогда
можно воспользоваться формулой вида
.
Тогда
можно воспользоваться формулой вида 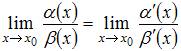 ,
то есть
,
то есть 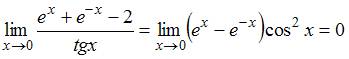 .
.
Тема: Непрерывность функции, точки разрыва Точка разрыва функции равна …
|
|
|
2 |
|
|
|
– 1 |
|
|
|
3 |
|
|
|
0 |
Решение:
Данная
функция определена и непрерывна на
каждом из интервалов ![]() и
меняет свое аналитическое выражение в
точках
и
меняет свое аналитическое выражение в
точках ![]() и
и ![]() Поэтому
функция может иметь разрыв только в
этих точках. Исследуем их на
непрерывность.
Для точки
Поэтому
функция может иметь разрыв только в
этих точках. Исследуем их на
непрерывность.
Для точки ![]() вычислим
односторонние пределы и значение функции
в этой точке:
вычислим
односторонние пределы и значение функции
в этой точке:
![]() ,
,
![]() ,
и
,
и ![]() .
Так
как
.
Так
как ![]() ,
то точка
является
точкой непрерывности данной функции.
Для
точки
вычислим
односторонние пределы и значение функции
в этой точке:
,
то точка
является
точкой непрерывности данной функции.
Для
точки
вычислим
односторонние пределы и значение функции
в этой точке:
![]() ,
,
![]() ,
и
,
и ![]() .
Так
как
.
Так
как ![]() ,
то точка
является
точкой разрыва первого рода.
,
то точка
является
точкой разрыва первого рода.
Тема: Непрерывность функции, точки разрыва Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Решение: Вычислим односторонние пределы функции в точке : , . Так как один из односторонних пределов в точке , а именно , то точка является точкой разрыва второго рода.
Тема:
Приложения определенного интеграла
Длина
дуги кривой ![]() от
точки
от
точки ![]() до
точки
до
точки ![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Длина
дуги плоской кривой
,
ограниченной прямыми ![]() ,
, ![]() ,
определяется по формуле
,
определяется по формуле 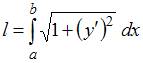 .
В нашем случае
,
,
а
.
В нашем случае
,
,
а![]() .
Тогда
.
Тогда
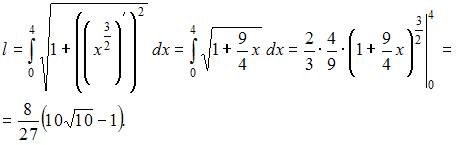
Тема: Дифференциалы и теоремы о дифференцируемых функциях Приближенное значение функции при , вычисленное с использованием дифференциала первого порядка, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Воспользуемся
приближенной формулой:
![]() .
Полагая
.
Полагая ![]() ,
, ![]() ,
приходим к равенству
,
приходим к равенству
![]() .
Вычислив
последовательно
.
Вычислив
последовательно
![]() ,
,
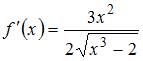 и
и 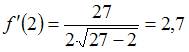 ,
получаем:
,
получаем:
![]() .
.
Тема: Дифференциальное исчисление ФНП Смешанная частная производная второго порядка функции имеет вид …
Тема: Дифференциальное исчисление ФНП Полный дифференциал функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть . Тогда
Тема: Непрерывность функции, точки разрыва Точка разрыва функции равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Данная функция определена и непрерывна на каждом из интервалов и меняет свое аналитическое выражение в точках и . Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность. Для точки вычислим односторонние пределы и значение функции в этой точке: , , и . Так как , то точка является точкой непрерывности данной функции. Для точки вычислим односторонние пределы и значение функции в этой точке: , , и . Так как , то точка является точкой разрыва первого рода.
Тема: Приложения определенного интеграла Площадь фигуры, изображенной на рисунке равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Площадь
данной фигуры можно вычислить по
формуле
,
где ![]() ,
, ![]() ,
, ![]() .
Тогда
.
Тогда
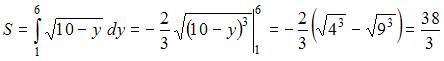 .
.
Тема: Дифференциалы и теоремы о дифференцируемых функциях Дифференциал второго порядка функции равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Дифференциал
второго порядка
функции
выражается
формулой
.
Тогда, вычислив ![]() и
и 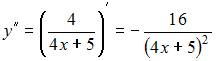 ,
получаем, что
,
получаем, что 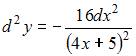
ДЕ5.Функциональный анализ
Тема:
Мера плоского множества
Мера
плоского множества ![]() равна
0
равна
0
Решение: В условии дана окружность радиуса 1, то есть кривая. Ее мера равна нулю.
Тема:
Элементы теории множеств
Даны
два множества
и
.
Тогда количество целых значений![]() ,принадлежащих
пересечению множеств А и В равно 4.
,принадлежащих
пересечению множеств А и В равно 4.
Тема:
Метрические пространства
Функция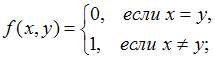 заданная
на множестве целых чисел …
заданная
на множестве целых чисел …
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
Тема: Отображение множеств Прообразом множества при отображении является
Тема:
Элементы теории множеств
Даны
два множества: ![]() и
и![]() .Тогда
количество целых значений х , принадлежащих
объединению множеств А и В, равно …8
.Тогда
количество целых значений х , принадлежащих
объединению множеств А и В, равно …8
Тема:
Мера плоского множества
Мера
плоского множества, изображенного на
рисунке,
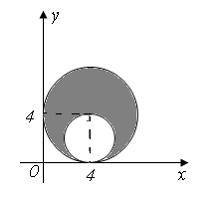
Равна ![]() .
.
Решение:
Мера
плоского множества равна площади
соответствующей фигуры, то есть для ее
определения из площади круга радиуса
4 нужно вычесть площадь круга радиуса
2. Следовательно, мера этого множества
равна ![]()
Тема:
Метрические пространства
Функция ![]() ,
где
и
,
….
не
удовлетворяет аксиоме треугольника
,
где
и
,
….
не
удовлетворяет аксиоме треугольника
не удовлетворяет аксиоме симметрии
не удовлетворяет аксиоме тождества
удовлетворяет всем трем аксиомам метрического пространства
Решение: Функция не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
Тема:
Отображение множеств
Биективное
отображение отрезка ![]() на
отрезок
на
отрезок ![]() может
быть задано функцией …
может
быть задано функцией …![]()
Тема:
Метрические пространства
Расстояние
между функциями ![]() и
и ![]() пространства
всех непрерывных действительных функций,
определенных на отрезке
пространства
всех непрерывных действительных функций,
определенных на отрезке![]() ,
с метрикой
,
с метрикой ![]() ,
равно…3
,
равно…3
Решение: ![]()
Тема:
Отображение множеств
Отображение,
действующее из отрезка
на
действительную числовую ось и имеющее
обратное отображение, может быть задано
функцией … ![]()
Решение: Функция, действующая из отрезка на действительную числовую ось и имеющая обратную, должна быть непрерывной и монотонной на . Например, это функция
Тема:
Мера плоского множества
Мера
плоского множества ![]() равна
…
равна
…![]()
Решение: Мера плоского множества равна площади соответствующей фигуры, изображенной на рисунке:
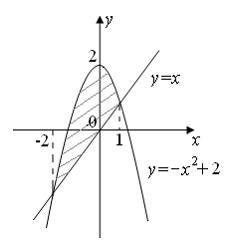
Вычислим
ее с помощью определенного интеграла. 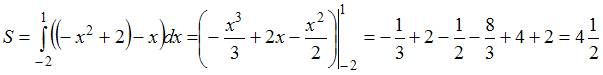
Следовательно,
мера этого множества равна ![]()
Тема:
Отображение множеств
Отображение
действует
по правилу: 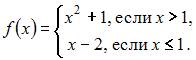 Тогда
имеет
вид …
Тогда
имеет
вид …![]()
Решение:
Так
как ![]() при
и
при
,то
при
и
при
,то![]()
Тема: Метрические пространства Функция , где и , …
|
|
|
не удовлетворяет аксиоме треугольника |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
Решение: Функция , где и , не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
Тема:
Элементы теории множеств
Даны
три множества: ![]() ,
, ![]() и
и ![]() .
Тогда число элементов множества
.
Тогда число элементов множества ![]() равно
…
равно
…
|
5 | |
Решение:
Выполним
операцию в скобках, то есть определим
множество ![]() .
Теперь выполним объединения
.
Теперь выполним объединения ![]() ,
в результате которого получится множество
чисел
,
в результате которого получится множество
чисел ![]() .
Таким образом, множество
содержит
пять элементов.
.
Таким образом, множество
содержит
пять элементов.
Тема: Мера плоского множества Мера плоского множества , где А= и равна …
|
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Решение: Мера плоского множества равна площади соответствующей фигуры, то есть квадрата со стороной 2. Мера плоского множества равна площади соответствующей фигуры, то есть круга с радиусом 1. Так как круг целиком лежит внутри квадрата, то искомая мера равна
Тема:
Элементы теории множеств
Даны
множества: ![]() и
и ![]() .
Тогда число элементов, принадлежащих
их пересечению равно …
.
Тогда число элементов, принадлежащих
их пересечению равно …
|
3 | |
Решение:
![]() .
Определим множество
.
Определим множество ![]() .
Получили множество, состоящее из трех
элементов.
.
Получили множество, состоящее из трех
элементов.
Тема: Мера плоского множества Мера плоского множества равна …
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
Решение:
Мера
плоского множества
равна
площади соответствующей фигуры,
изображенной на рисунке:
 Вычислим
ее с помощью определенного
интеграла.
Вычислим
ее с помощью определенного
интеграла. 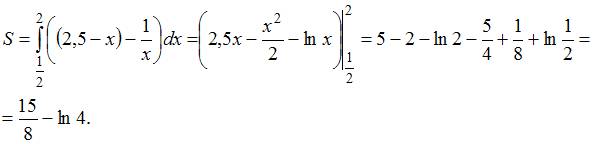 Следовательно,
мера этого множества равна
Следовательно,
мера этого множества равна ![]() .
.
Тема: Элементы теории множеств Даны два множества: и . Тогда количество целых значений , принадлежащих пересечению множеств и , равно …
|
4 | |
Решение: Пересечением множеств и является промежуток [-1; 3), который содержит четыре целых числа.
Тема: Метрические пространства Функция , где и , …
|
|
|
не удовлетворяет аксиоме треугольника |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
Тема: Отображение множеств Пусть задано отображение . Тогда имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
По
определению прообраза множества ![]() .
Тогда
.
Тогда![]()
Тема:
Элементы теории множеств
Даны
множества: ![]() ,
, ![]() .
Тогда число целых чисел, принадлежащих
их объединению равно …
.
Тогда число целых чисел, принадлежащих
их объединению равно …
|
9 | |
Решение:
![]() .
.
![]() .
Таким образом, объединение содержит
девять элементов.
.
Таким образом, объединение содержит
девять элементов.
Тема:
Мера плоского множества
Плоская
мера множества ![]() равна
…
равна
…
|
|
|
0 |
|
|
|
32 |
|
|
|
8 |
|
|
|
18 |
Тема: Метрические пространства Расстояние между функциями и пространства всех непрерывных действительных функций, определенных на отрезке , с метрикой , равно …
|
|
|
3 |
|
|
|
– 2 |
|
|
|
1 |
|
|
|
|
Тема:
Отображение множеств
Обратимым
на ![]() является
отображение …
является
отображение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Отображение ![]() называется
обратимым, если существует отображение
называется
обратимым, если существует отображение ![]() такое,
что
такое,
что ![]() ,
где
,
где ![]() –
тождественные отображения на
множествах
и
соответственно.
По
критерию обратимости: отображение
будет
обратимым, если оно инъективно и
сюръективно.
Отображение
на
отрезке
не
инъективно, например, для точек
и
–
тождественные отображения на
множествах
и
соответственно.
По
критерию обратимости: отображение
будет
обратимым, если оно инъективно и
сюръективно.
Отображение
на
отрезке
не
инъективно, например, для точек
и ![]() образы
совпадают:
образы
совпадают: ![]() .
Отображения
и
также
не инъективны, например, для точек
и
.
Отображения
и
также
не инъективны, например, для точек
и ![]() в
обоих случаях
в
обоих случаях ![]() .
Отображение
.
Отображение 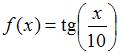 инъективно
(для
инъективно
(для ![]() )
и сюръективно (отрезок
переходит
в отрезок
)
и сюръективно (отрезок
переходит
в отрезок 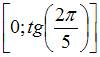 );
обратным для него будет отображение
);
обратным для него будет отображение ![]()
Тема: Мера плоского множества Мера плоского множества равна …
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
Решение: В условии дана окружность радиуса 1, то есть кривая. Ее мера равна нулю.
Тема: Отображение множеств Отображение действует по правилу: Тогда имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы теории множеств Даны множества: и . Тогда число элементов, принадлежащих их пересечению равно …
|
3 | |
Решение: . Определим множество . Получили множество, состоящее из трех элементов.
Тема: Отображение множеств Обратимым на является отображение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы теории множеств Даны два множества: и . Тогда количество целых значений , принадлежащих пересечению множеств и , равно …
|
4 |
Тема: Метрические пространства Расстояние между функциями и пространства всех непрерывных действительных функций, определенных на отрезке , с метрикой , равно …
|
|
|
3 |
Тема: Элементы теории множеств Даны три множества: , и . Тогда число элементов множества равно …
|
1 | |
Решение: Определим множество и выполним операцию пересечения . В результате получится множество , состоящее из одного элемента.
Тема:
Отображение множеств
Прообразом
множества ![]() при
отображении
при
отображении ![]() является
…
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Прообразом
множества
при
отображении
являются
те точки
,
которые при данном отображении попадают
в отрезок
,
то есть множество ![]() .
.
Тема: Мера плоского множества Плоская мера отрезка [0; 1], лежащего на оси в плоскости равна …
|
|
|
0 |
|
|
|
1 |
|
|
|
бесконечности |
|
|
|
несчетна |
Решение: Плоская мера отрезка [0; 1], лежащего на оси в плоскости равна нулю.
Тема: Метрические пространства Расстояние между точками и в метрике , где и равно 4
ДЕ6.Комплексный анализ
1) Области на комплексной плоскости
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке,
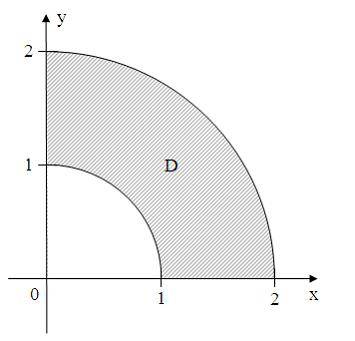
удовлетворяют условию …
![]()
2) Дифференцирование функции комплексного переменного
Значение
производной функции 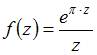 в
точке
в
точке![]() равно
…
равно
…
![]()
Решение: Производная функции имеет вид
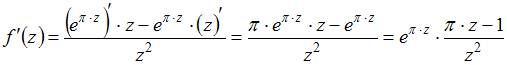 .
.