
- •1 Цілі і завдання загальної освіти і цілі навчання математиці в загальноосвітній школі
- •Внутріпредметні та між предметні зв’язки.
- •2 Характеристика основних методів навчання математики : пояснювально-ілюстративний , репродуктивний , проблемний , Метод доцільних задач.
- •3. Типи уроків та їх структура.Викладання математики за лекційно-практичною системою.
- •4 .Вимоги до сучасного уроку математики в школі. 5-6 кл, 7-9 кл.
- •5.Діяльнісний підхід до навчання мат-ки. Аналіз, синтез, порівняння.
- •6. Методика формування математичних понять в шкм .Види означень в шкм.
- •7. Методика навчання учнів дов-ня мат тверджень .Теореми . Методика доведення теорем у шкм.
- •8.. Задачі в навчанні мат-ки. Методика роз’язування математичних задач.
- •9. Контроль знань та вмінь учнів з математики . Основні вимоги до контролю в умовах диференціального навчання .Види тестів і їх характеристика .
- •10. Методика вивчення натуральних чисел Десяткових дробів і процентів. Методика вивчення звичайних дробів . Методика вивчення дійсних чисел.
- •11. Поняття про ірраціональне число і множину дійсних чисел. Методика викладання тотожних перетворень ірраціональних виразів.
- •12. Рівняння та нерівності в основній школі і методика їх вивчення.Методика вивчення дробово-раціональних рівнянь та нерівностей. Метод інтервалів.
- •13. Функціональна пропедевтика (математика 5-6 кл.) Функції у курсі алгебри основної школи.
- •14. Методика вивчення тригонометричних рівнянь і нерівностей.Методика вивчення тригонометричних ф-цій.
- •16 Методика розв’язування задач на побудову . Основні методи .
- •Метод гмт.
- •Метод паралельного перенесення:
- •Алгебраїчний метод:
- •18. Методика введеня теми „перетворення подібності”.
- •19.. Методика проведення перших уроків планіметрії
- •20. Координати і вектори на площині.
- •22.Методика вивчення тем "Паралельність прямих на площині". Сума кутів трикутника.
- •23. Методика введеня теми „Подібність фігур”.
- •24. Методика вивчення теми чотирикутники.Методика вивчення многокутників.
11. Поняття про ірраціональне число і множину дійсних чисел. Методика викладання тотожних перетворень ірраціональних виразів.
За чинною програмою треба вивчати ірраціональні числа і множину дійсних чисел у 8 клас на доступному рівні за короткий час , без багатьох означень і доведень або фактично на рівні уявлень . Тому мотивання і введення ірраціональних чисел можна здійснити таким методичним варіантом.
На одиничному відрізку координатної прямої будується квадрат і ставеться за мету визначити довжину його діагоналей ОК , а відповідне число зобразити точкою Р на координатний прямій.Геометрично це виконується легко відкладанням циркулем відрізка ОК на координатній прямій.Однак виникає запитання : яким чином виражається координата точки К . Щоб з’ясувати це , позначимо довжину відрізка ОК буквою х і побудуємо ще один квадрат , стороною якого є відрізок ОК . З рисунка видно , що площа квадрата вдвоє більша за площу одиничного квадрата . Одже , х2=2, оскільки площа одиничного квадрата дорівнює 1.
Щоб визначити х ,треба розв’язати одержане квадратичне рівняння. Геометричний спосіб розв’язання свідчить про те , що існують два корені цього рівняння . Квадрат кожного з них дорівнює 2. З попереднього матеріалу учні вже знають , що число , квадрат якого дорівнює 2, наз. Квадратним коренем. Арифметичний квадратний корінь позначається символом . Тому два корені рівняння х2=2 є не що інше як числа . Які це числа.
Далі формується і доводиться методом від супротивного твердження : не існує раціонального числа , квадрат якого дорівнює 2. Отже , корені рівняння не належать до раціональних чисел , Звертається увага на те , що не є ірраціональними числа також . Такі числа називаються ірраціональними. ( можна обчислити з якою завгодно к-тю десяткових знаків наближене значення числа , можна показати на калькуляторі)
Ірраціональних чисел можна утворити безліч , якщо записувати неперіодичний десятковий дріб . Інакше і бути не може , бо тоді б вони були числа раціональні.
Якщо множину раціональних чисел доповнити ірраціональними , то одержана множина називається множиною дійсних чисел і позначається буквою . У множині дійсних чисел виявилась можливою дія добування корення з раціональних чисел і деякі інші математичні операції.
В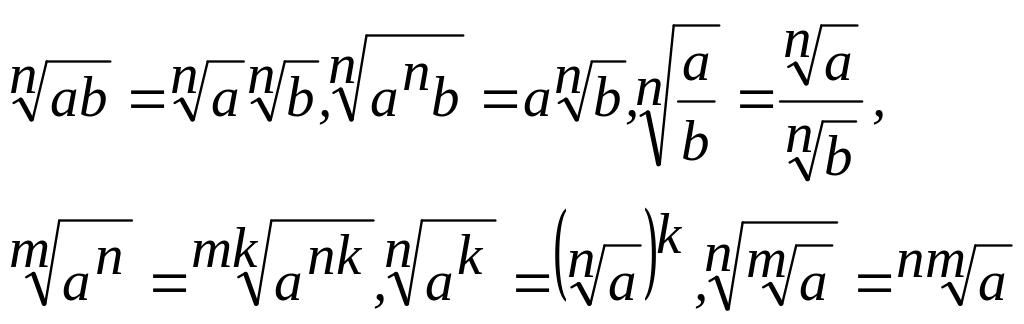 перше
з
ірраціональними виразами
учні ознайомлюються в 8 кл. під час
вивчення квадратних коренів. Вирази ,
які містять дію добування кореня зі
змінної або виразу, який містить змінну
наз. ірр.в. на цьму етапі навчання мають
справу лише з ірр. в. які містять
арифметичні квадратні корені. Вирази
які містять корені будь- якого степеня
вивчаються в курсі алгебри і поч..а. Як
відомо, квадратний корінь, наприклад,
з числа 25 має два значення: 5 і —5. Тому
іноді пишуть: √25 = ±5. Такий запис
неправильний, бо домовились під символом
√25 розуміти тільки арифметичний корінь.
Символ √ треба вводити не зразу після
пояснення квадратного кореня, а
пізніше, коли буде введено поняття
арифметичного кореня. Тоді ж можна
розглянути і тотожність (√а)2
=|a|
ця рівність справедлива при всіх
значеннях а.
перше
з
ірраціональними виразами
учні ознайомлюються в 8 кл. під час
вивчення квадратних коренів. Вирази ,
які містять дію добування кореня зі
змінної або виразу, який містить змінну
наз. ірр.в. на цьму етапі навчання мають
справу лише з ірр. в. які містять
арифметичні квадратні корені. Вирази
які містять корені будь- якого степеня
вивчаються в курсі алгебри і поч..а. Як
відомо, квадратний корінь, наприклад,
з числа 25 має два значення: 5 і —5. Тому
іноді пишуть: √25 = ±5. Такий запис
неправильний, бо домовились під символом
√25 розуміти тільки арифметичний корінь.
Символ √ треба вводити не зразу після
пояснення квадратного кореня, а
пізніше, коли буде введено поняття
арифметичного кореня. Тоді ж можна
розглянути і тотожність (√а)2
=|a|
ця рівність справедлива при всіх
значеннях а.
Переважну більшість тотожних перетворень іррац. виразів виконують, користуючись теоремами про радикали (для додатних а, Ь) звичайно записують так:
У 8 класі розглядають лише деякі з цих тотожностей до того ж тільки з квадратними коренями. Майже всі ці співвідношення доводять однаково, тому ми спинимось на доведенні першого з них для n = 2.
Щоб довести при невід'ємних значеннях а, b тотожність піднесемо обидві частини цієї рівності до квадрата: Як бачимо, квадрати обох частин рівні, тому тотожність справедлива. Міркування було б правильне, коли б ми підкреслили, що обидві частини доводжуваної рівності – числа додатні, а перед цим довели таку лему: якщо квадрати додатних чисел рівні самі числа. Після доведення цієї тотожності учням ще раз треба нагадати що а, Ь — невід'ємні числа. З найхарактерніших помилок, що їх допускають учні в перетворенні ірраціон. виразів є неправильне винесення множників з-під знаку кореня і неправильне внесення множників під знак кореня.
Учні
вважають, що рівність а√в=√а2в
справедлива при всіх числових значеннях
а, зокрема і при відємних
![]()
Розв’язати систему вправ 1) винесення мн-на за знак кореня, 2) внесення множника під знак кореня, 3) якщо знак кореня міститься в знаменику дробу, такий дріб можна замінити тотожнім йому дробом, знаменник якого не містить коренів, досить домножити члени дробу на відповідно підібраний вираз, такі перетворення наз. звільненням дробу від ірраціональності.
