1. Компонентный анализ и 2. Выделение главных компонент

1. Компонентный анализ

Задача следующая: Имеется пространство в котором задана выборки (единый элипс рассеяния).Необходимо найти новые взаимно ортогональные оси так, чтобы дисперсии проекций точек на были максимальны:

- вдоль первой надо получать максим. по сумме расброса точек

- – д.б. ортогональна и при этом иметь вдоль себя также проекции с макс. расбросом и т.д. до с

Вспомним варианты расположения эллипса рассеяния в координатах

На рис 1 - круг рассеяния – х-ы независимы и дисперсии по каждой оси одинаковы – на какую новую ось не проектируй – получишь те же шарики – вид сбоку.

На рис 2. х-ы независимы, то есть матрица ковариаций диагональная . Оси эллипса рассеяния расположены паралельно осям координат - поэтому в данном случае мы имеем уже решенную задачу КА – так как оси рассеяния элипса паралельны осям координат х и удовлетворяют условиям задачи КА

Теперь нам понятна задача КА–

Когда имеем общий случай элипса рассеяния в Х – рис 3 и матрица ковариаций недиагональна то нашей целью есть получить новые координаты в У

такие чтобы все выглядело в них как на рис 2.

То есть сначила найти ось у₁ по макс. расброса рис 4 Затем ортоганальную ей у₂ по макс расброса рис 5. и так далее с тем чтобы получить в новых координатах у рис 5 положение элипса рассеяния так как оно расположено в старых координатах х на рис. 2

Каким образом решать такую задачу.

Запишем - сумму ср. квадр отклонений точек на оси : Если выразим что то если обознач

, и , то есть это -тая строка матрицы , то в вект. виде получим

или где -ковариационная матрица переменных х

(вспомним о золотой матрице ковариаций – центрированной Х^TХ)

Для однозначности нахождения наилучшего и соответствующего уравнения прямой проекции вводят условия нормировки и нам надо найти решение

Справа мы имеем квадратичную форму и можно было бы- как нам привычно (МНК)– взять производную по составляющим вектора и решать соответствующую систему для его определения.

Однако

Так мы найдем только первую главную компоненту. – ту вдоль которой имеется наибольший расброс точек в Х - рис. 4. Но нам надо найти и другие компоненты –

А вторая компонента , будучи ортогональна первой должна иметь направление при этом вдоль максимального расброса в оставшихся направлениях пространства

Для того чтобы решить эту задачу надо вычислить остатки и для них , как ранее на х-ах, построить матрицу ковариаций и снова решить задачу макс. уже при условии нормировки и ортоганальности (*)

Задача посложнее – доп операции по вычислению остатков и

учет дополнительного ограничения (*)

Далее – для третьей оси - снова вычисление остатков и новая поцедура поиска уже вектора . В целом имеем серию процедур последовательной максимизации - на дисперсии остатков от процедуры N =( ) при условии н нормировки и учета условия ортогональности векторов

Все это не очень технологично.

Роль спектральной теоремы в решении задачи компонентного анализа

Но оказывается задачу КА

поиска наибольших дисперсий по взаимно ортогональным направлениям возможно решить в терминах собственных значений и собственных векторов матрицы ковариаций . Вернее более правильно так ------

– известно (из лин алгебры) что для любой положительно определенной матрицы существует преобразование ее в диагональную матрицу : (**) причем ее диагональные элементы есть - собственные числа матрицы , а - матрица ее собственных ее векторов

Выражение (**) называют спектральной теоремой или спектральным разложением матрицы

Если в качестве мы возьмем матрицу ковариаций , то -будут одновременно и СбствЧ и наилучшие дисперсии на осях пространства пространства (на рис 5) из переменных , где - строки матрицы собств. векторов , а в силу того что они налучшие дисперсии, удовлетворяют

Тогда можно применить известный для нас механизм нахождения СЧ и СВ

(вставка о сб.ч. и сб.в.)

1.решаем – это условие нахождения собственных чисел и находим ( это одновременно наши наилучшие дисперсии)

2.затем в условие для собственного вектора (*)

подставляем получая (**)

Решая последовательно (**) для каждого находим все вектора которые есть и направляющие линий проекции

Однако приведенные чисто алгебраические методы поиска и тоже не очень технологичны – например при 10-м порядке матрицы для получения надо решать уравнение десятой степени и находить 10 его корней и тд.

Поэтому для нахожднния и применяют другой приближенный, но достаточно изящный подход

Посмотрите на рис 3 У данного элипса рассеяния недиагональная матрици ковариаций

Если мы найдем целесообразный метод вращения координат то в результате найдутся новые положения осей как на рис 5 что в них элипс будет стоять уже как на рис 2 а значит в преобразованных координатах будем иметь диагональную ков. матрицу , где по диагонали стоят искомые дисперсии (собств. числа ) а итоговая матрица преобразования в будет искомой матрицей собственных векторов и одновременно направляющими линий проекции . Для вращения применяется метод Якоби.

Напомним что рассмотренный выше этап МГК где находятся эти новых компоненты называется компонентным анализом -КА

2. Этап МГК – выделение главных компонент

Построение главных компонент … реализуется так, что полученные и соответственно были упорядочены на диагонали по величине, поэтому нам интересны именно первые несколько - наиболее концентрировавшие в себе дисперсию данных.

Именно они называются главными компонентами и именно их число используют в дальнейшем для анализа.

Число главных компонент q

Наиболее распространенных критерия выбора числа ГК – 2 .

1 .Критерий Кайзера (Kaiser, 1960) Основан на учете того, что процедуры преобразования проводятся не с ковариционной а с корелляционной матрицей – где по диагонили (дисперсии) стоят 1.

Т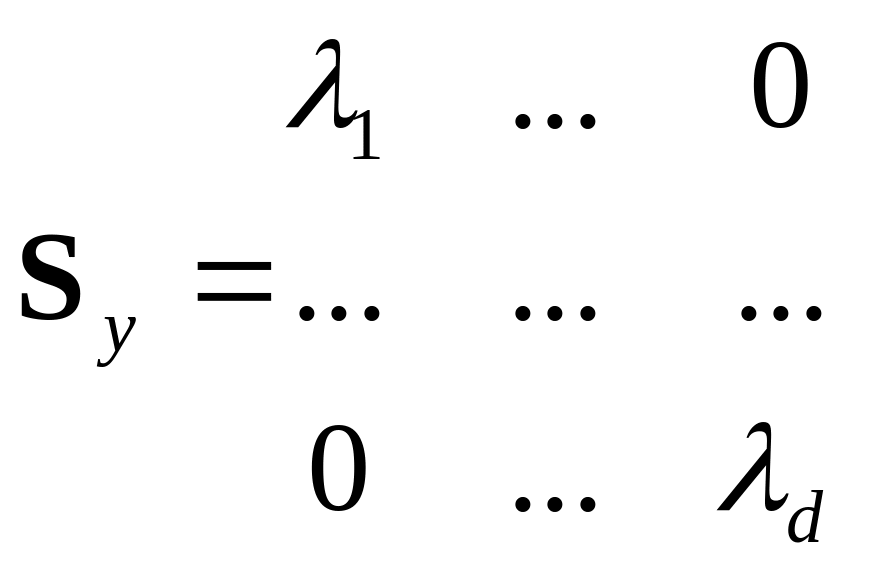 аким образом в преобразованной матрице , где на диагонали тоже будут стоять дисперсии – их величина отражает относительное перераспределение

дисперсий - от ряда дисперсий 1 1 1 1 1 1 к кряду допустим 4 1 0.5 0.2 0.1 0.1

По данному критерию считается достаточным выбрать число компонент с величиной . Здесь это 2 компоненты.

2 . Другой распространенный критерий – критерий Кэттеля (Cattell,1966) или критерий каменистой оссыпи. Строят зависимость :

по оси у- величина по оси х – номер компон. .

Количество компонент выбирается на том месте оси номеров компонент где излом графика наиболее резко переходит к основной затихающей тенднции :

Здесь число главных компонент - 4

Таким образом определяется целесообразная размерность нового сокращенного ортогонального пространства признаков.

Еще раз зачем нужен МГК. – Это метод целесообразного сокращения количества координат пространства. Вместо исходного d мерного в рассмотрение берется небольшое количество новых координат с наибольшими , в которых сконцентрирована и отражается львиная часть исходной дисперсии Х-ов. .

То есть будем оперировать в дальнешем только ГК вытеснив незначимые компоненты и, игнорируя по сути, шумовые составляющие Х.

Оценка эффективности процедуры МГК

– Эффективность МГК покажет насколько точно с помощью новых компонент представлены старые d штук х. Это возможно расчитать , записав обратные зависимости – переменных х от главных компонент у.

Ниже будем называть полученные новые переменные уже не компонентами Y (как выше в компонентном анализе - ) а факторами F как это принято в ФА.

X_i=A_i1F₁+A_i2F₂+...+A_iqF_q+U_i, (*)

В матричном виде X=AF+U,

Где F называют матрицей счетов, А-матрицей факторных нагрузок, F_1…..F_q - общими факторами а U_i- характерными факторами.

U_i по построению (как остатки) предполагаются некоррелированными друг с другом и с общими факторами.

Построив систему (*) оценивают

процент общности определенный общими факторами и

остаток - процент шума вносимый характерными факторами

Внимание

Здесь заканчивается МГК. – далее другие процедуры ФА

Процедуры вращения в ФА (

Дальнешие процедуры ФА отказываются от конструкции факторов как концентрирующих максимум исходной дисперсии признаков и применяют механизм их линейной деформации (вращения) так, что-бы исходные Х сгруппировались (по возможности) в “группы по интересам” – факторам.

Цель – найти положение факторов так что-бы все максимально компактно разделились на “группы влияния” - (условно -подмножества ) в каждом из которых какие-то входят в “свой” фактор . с большими нагрузками , а остальные (не входящие в подмножество фактора ) в данный фактор входят с малыми нагрузками .

Визуальное выделение групп переменных и интерпретация факторов.

Группы переменных разделились по факторам как только мы определилисть с количеством факторов, получили систему (*) и произвели какую-то версию их вращения.

Но для того чтобы увидеть эти группы факторов надо проанализировать величины факторных нагрузок в каждой из исходных переменных.

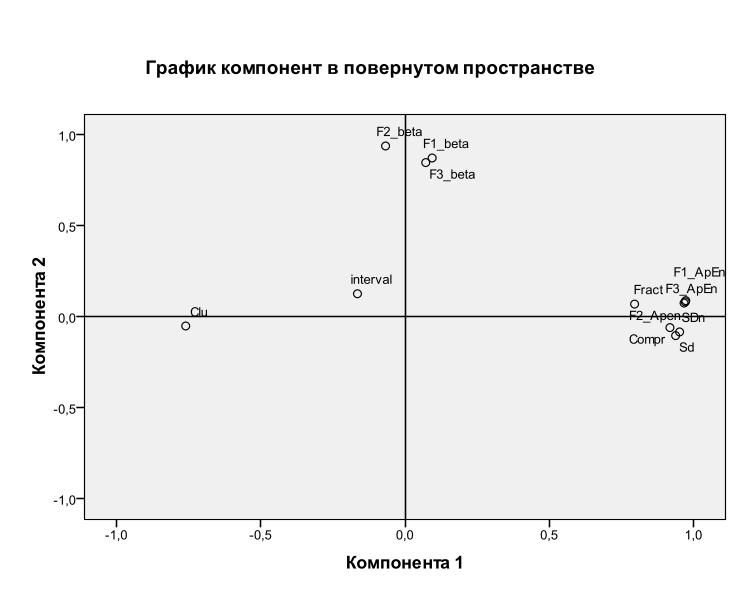
Факторные нагрузки являются инструментом для предметной интерпретации факторов. Увидеть группировки х-ов можно на графике в постранстве нагрузок факторов.

В постранстве нагрузок факторов (если их 2) изображаются переменные х точкой (вектором) и видно как группы “по интересам” ”прижимаются” к соответствующим осям факторов (на рисунке-компонент), большая нагрузка - большая кореляция с данным фактором).

При выделении более 2-х факторов увидеть сформировавшиеся группы переменных можно из таблицы нагрузок факторов – в SSPS название таблиц – Component Matrix (Матрица компонент) после поворота фактoров – Rotated Component Matrix (Матрица повернутых компонент).

Затем надо попытаться обобщить предметный смысл каждой такой выделенной группы переменных и на основе этого сформулировать предметный смысл соответствующего фактора

Критерии целесообразностии ФА

Ну и последнее. Все описанные процедуры ФА целесообразны, если признаки Х достаточно сильно кореллированы. Тогда эфективна задача МГК - можно перераспределить дисперсии х в несколько ГФ - главных факторов,

А вращение факторов поможет найти такое их положение, что каждый из факторов будет зависеть в основном только от выделившейся группы кореллированных переменных х.

Однако если исходные х-ы слабо кореллированы, то “не тратьте куме сили” – их перераспределять, а пуще того, вращать – бессмысленно, – исходные х-ы уже практически факторы, -“ вже маэмо, що маэмо”.

Для оценки ситуации стоит или не стоит провадить ФА оценивают матрицы корреляций х, то есть оценивают - какая присутствует степень связанности исходного пространства в Х. Наиболее показательны следующие критерии -

критерий сферичности Бартлетта-Уилкса и критерий адекватности выборки Кайзера.

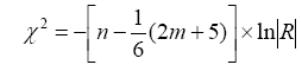1. Критерий сферичности Бартлетта-Уилкса

где n – объем выборки, m – число переменных, ln – натуральный логарифм, |R| - определитель матрицы корреляций, cтепень свободы

С помощью критерия проверяется гипотеза о том что корр. матрица есть единичной матрицой то есть , в которой все элементы главной диагонали равны 1, а все остальные – нулю – то есть нет парных корреляций.

Ориентируются при этом на величину коэффициента сферичности и уровня значимости . Если этот коэффициент достаточно велик, а соответствующий ему уровень значимости мал (p< 0.05 ), то это свидетельствует о надежном отличии корреляционной матрицы от единичной. При высоком уровне значимости - ставится под вопрос адекватность использования ФА с имеющимися данными.

Однако возможных причин неэффективности ФА больше:

Малое количество х, замусоренность пространства х практически идентичными переменными, включенность в состав Х посторонних, некоррелированних переменных и тд. Все это в целом позволяет оценить

2.! Мера адекватности выборки Кайзера-Мейера-Олкина (КМО)

Статистика теста определяет отношение общей дисперсией, (т.е. дисперсии которая определена общими факторами) к полной дисперии данных. Критерий оценивает насколько парная корреляция исходных переменных х может быть объяснена факторами

Т.о. критерий оценивает адекватность факторной модели набору переменных, составившему данную корреляционную матрицу – стоит ли делать факторный анализ с этими данными.

Значения КМО по 6-бальной шкале оценивают следующим образом:

0.9-"отличные",0.8 -"хорошие",0.7-"средние",0.6-"посредственные" , 0.5 -"плохие", а ниже 0.5 - неприемлемые".

Для оценки вклада в “неединичность” корреляционной матрицы каждой переменной х в отдельности используют меру выборочной адекватности ( коэффициент MSA в системе SPSS- это индивидуальный КМО для каждой переменной). Бальные характеристики Кайзера справедливы для оценки и этих величин тоже. Оценки по MSA каждой переменной позволяют исключить из расчетов одну или несколько переменных, и тем самым повысить результативность ФА.

Выводы по ФА

Аппарат ФА - достаточно субъективен (за что его и критикуют) . Вращение чаще применяют ортогональное (в SPSS-“варимакс”)

- полученные Главные Компоненты вращают, оставляя их при этом взаимно ортогональными

и косоугольное, допуская их не ортогональность – лишь бы полученные факторы были тесно кореллированы с образуемой “группой влияния” Х-ов,

Общий принцип – лишь бы попасть на красивую интерпретацию факторов как латентной причины группы “по интересам” следствий – х-ов.

Однако плюсы ФА перевешивают минусы – симбиоз грамотного предметного специалиста и математического аппарата ФА часто попадает в цель и получают очень красиво интерпретируемые результаты внутренней структуры изучаемого явления.

Из-за недостатка времени и указаной субъективности аппарата вращения мы не будем подробно останавливатся на всех разновидностях механизма образования факторов – с ними коротко можно познакомится в самоучителе по ssps, а мы прогоним на практике через ФА в ssps, наши данные и посмотрим результаты группировки переменных в факторы.

Резюме – инструмент ФА – это инструмент выявления скрытых латентных причин (факторов F) каждый из которых должен наилучшим образом объяснять нам изменения, вариации в переменных (следствиях, признаках) х в корреллированных “по интересам” группах х-ов

Канонический ДА

Общее и различия в постановке и принципе решения задач КДА и ФА

В КДА также как в МГК ищутся некоторое количество ортогональных осей на которых с точки зрения эффективности разделения подмножеств Х_1,…,Х_К точек множества , , Х₁= j=1,n₁ …Х_К= j=1,n_к положение проекций этих точек оптимально.

З адача таким образом аналогично в МГК сводится к некоторому условию

решение которого определит нам и качество критериев и положение осей

А механизм получения такого решения нам уже знаком – вращение осей исходного пространства Х до тех пор пока вместо положительно определенной матрицы не получим диаг. матрицу .

На ее диагонали - нужные нам , а итоговая матрица преобразования есть матрица собств. векторов и одновременно направляющие осей .

Есть и особенности задачи КДА относительно задачи МГК.

1. Как определить критерий качества проекций точек х и соответствующую им матрицу отношения дисперсий .

– то есть, вид критерия , характеризующего эффективность положения прямых проекции с точки зрения разделимости классов, а также соответствующую им матрицу для которой -есть характеристич. числа, а собственные вектора которой будут направляющими линий проекции

2. Возможное количество этих линий проекции q - то есть размерность пространства дискриминационных функций

3.Критерии шаговой процедуры ДА для определения оптимального состава Х

4. Характеристики качества разделенности классов отд. приложение – методичка к SPSS

Рассмотрим последовательно эти особенности.

Определение критерия качества проекций в КДА и механизма расчета направляющих осей пространства дискриминантных функций.

1. Критерии качества проекций точек х на оси и соответствующая им матрица отношения дисперсий .

Определим интересующий нас показатель;

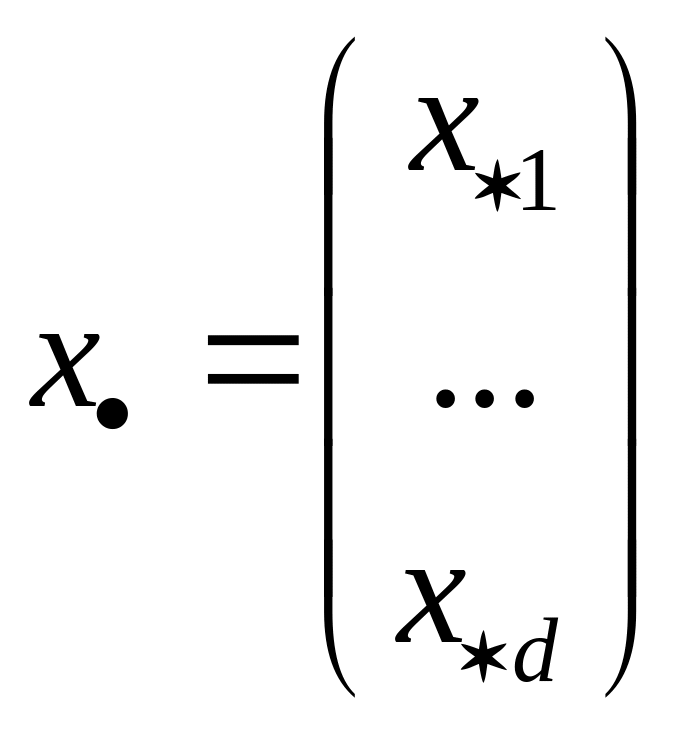1. Если вектор определен как строка матрицы то есть и -к-тый центроид в Х, то матрица разброса (ковариаций) внутри к-того класса

Матрица суммарного внутриклассового расброса

Напомним для дальнейшего, что ранг каждой матрицы образованной как внешнее произведение векторов (типа ВВ^Т )- не более 1. Докажите это.

Пример – = (*) и видим, что если вторую строку умножим на то получим первую строку. Т.о ранг (*) не более 1. и тд

Поскольку ранг каждой из не более единицы, и поскольку только К-1 из них – линейно независимы - (имея центры и к-1 матрицу данных … возможно ввостановить . Покажите это) то ранг матрицы суммарного внутриклассового расброса не более К-1

2 . Определим полный вектор средних значений в Х - m и полную матрицу разброса : и Тогда

Т ак как известно что полный разброс есть сумма разброса внутри класса и разброса между классами то

Тогда естественно определить второй член в (*) как - матрицу разброса между классами, :

Как и выше очевидно что ранг матрицы как и тоже не более чем К-1.

Как будет показано немного ниже из этого следует что максимальная размерность пространства проекции из Х^d в У^q будет не более чем К-1

То есть

Проекция из d-мерного пространства в (К-1)-мерное пространст­во осуществляется с помощью К-1 разделяющих функций

i=1, . . . , К-1 (88)

Если считать составляющими вектора , а векторы весовых функций столбцами матрицы размера d*(К-1), то проекцию можно записать в виде одного матричного уравнения

. (89)

Выборки x₁, . . ., х_n проецируются на соответствующее множе­ство выборок y₁, . . ., y_n которые можно описать с помощью их векторов средних значений и матриц разброса. Так, если мы опре­деляем

и

и

то можно непосредственно получить

(**)

Определим теперь интересующий нас показатель разделимости классов как отношение дисперсии межгрупповой к дисперсии внутригрупповой

(1) - Известно как частное Релея

на интересующих нас новых координатах

О чевидно что это

хороший показатель

- чем он выше тем лучше

разделяющие свойства данной линии у:

чем>числитель тем дальше центры друг от друга, чем< знаменатель тем более компактны группы.

Уравнения (**) показывают, как матрицы разброса внутри класса и между классами отображаются посредством проекции в простран­ство меньшей размерности.

Мы ищем матрицу отображения ,которая максимизирует

отношение разброса между классами к / разбросу внутри класса.

Простым скалярным показателем разброса является определитель матрицы разброса.

Определитель есть произведение собственных значений, а следова­тельно, и произведение «дисперсий» в основных направлениях, измеряющее объем гиперэллипсоида разброса.

Пользуясь этим пока­зателем, получим функцию критерия

(2)

Задача нахождения прямоугольной матрицы , которая мак­симизирует по (1) или (2) – известное как частное Релея, сводится к нахождению обобщенных собственных векторов, соответству­ющим наибольшим собственным значениям в

(**)

Несколько замечаний относительно этого реше­ния.

Во-первых, если — невырожденная матрица, то задачу, как и прежде, можно свести к обычной задаче определения собст­венного значения. То есть образуем из (**) или

То есть можем стандартно искать и как СобствЧисла и СобВек матрицы . Так мы можем решить задачу.

Однако в действительности так решать нежелательно, так как при этом потребуется ненужное вычисление матрицы . Вместо этого можно найти собственные значения как корни характеристического полинома (обобщенная задача определения СЗ)

,

обобщенная задача определения СЗ, а затем решить

непосредственно для собственных векторов v_i. Как решать далее дело вкуса в том числе можно

применить итерационный алгоритм вращения осей (метод Якоби)

получим как и прежде в ФА диагон. матрицу

собственных значений матрицы и соответстующую ей матрицу преобразований (собственных векторов)