2 . Линейное расстояние (манхеттенская мера) тоже выражение что и (п.1) но для общего случая

2 . Эвклидова мера – наше обычное расстояние в постранстве независимых координати равенстве дисперсий рассеяния в классах и по отдельным координатам

3. Обобщенное степенное расстояние Минковского

Из рис видно что

М анхэтенская мера подчеркивает а Минковского (Евклидова) сглаживает различия

4. Взвешенное Эвклидово расстояние

Признаки независимы и дисперсии равны в классах: , , но по отдельным дисперсии различны , ,

Матрицы ковариаций равны в классах и диагональны

– Эвклидовы расстояния равны до центров классов, но очевидно что отнести надо точку х к классу 2 (она ближе к границе рассеяния кл. 2)

По сути, это соответствует коррекции формулы расстояния на величину дисперсий которые отражают форму элипсов рассеяния объектов.

Т.О целесообразно корректировать расстояние до центров классов по данному направлению пропорционально и уже величине такого расстояния определять принадлежность к классу. Это частный случай расстояния Махаланобиса (см. Ниже)

5. Расстояние Махаланобиса

Е сли координаты зависимы – и рассеяния в классах одинаковы, то ковариационные матрицы в классах равны и недиагональны (обозн или )

имеем следующую картину –элипсы рассеяния ориентированы одинаково в классах но произвольно по направлениям.

Мы также видим что при равенстве Эвклидова расстояний от центров классов до точки х - точка более близка к границе 2-го класса

Для того чтобы эта близость следовала из меры расстояния до центров классов ее необходимо скорректировать подобным же образом как и в предыдущем случае,

- но используя не только даигональные элементы матрицы ковариаций – дисперсии, а всю матрицу ковариаций целиком.

Формула расстояния до центра класса теперь по аналогии с предыдущим случаем (но с учетом общего направления рассеяния) выглядит так

где - обратная матрица ковариаций. Эта общая формула расстояния носит название индийского математика Махаланобиса.

6. Ну и понятно что при неравенстве

матриц ковариаций в классах

будем иметь свою формулу расстояния

до соответствующего класса.

0 Вы уже заметили – что мы корректировали формулу расстояния с тем чтобы точку присвоить тому классу, граница рассеяния которой ближе к точке х - Вы уже поняли что методы построения формул границ и методы построения формул расстояний до центров имеют в своей основе нечто общее а именно

- построение формулы общности класса – и в этом

внутреннее единство обоих подходов к распознаванию.

7. Махаланобисово расстояние с учетом априорных вероятностей классов.

Для корректого отнесения точки к классу нужен учет плотности “заселения” элипсов рассеяния точками соответствующих классов = ведь в одном элипсе может быть -3 точки а в другом 333 – и если

это ОТРАЖАЕТ ЧАСТОТУ НАБЛЮДЕНИЯ КЛАСОВ то должно было бы учитыватся в механизме отнесения к классу.

Тогда величины 3\226 и 333\336 –можно принять как - априорные вероятности классов

Мы вилим термины “частота, вероятность” и понимаем что переходим к элементам Вероятностной Постановки.

Корректировка меры расстояния делается в предположении

1. нормальности распределения признаков в классах – и

2. использовании априорных верояностей .

Пока примите на веру что корректировка Растояния Махаланобиса с учетом апприорной вер имеет вид

Потом мы это покажем

Касательно использования отметим

1. Априорные вероятности оказывают основное влияние если есть перекрытия классов в Х, - то есть когда объекты с некоторыми вероятностями могут принадлежать ко многим группам. Если же группы сильно различаются в Х (далеко отстоят) , то предпосылок для применения ВП и априорных вероятностей - нет

2. В качестве априорных вероятностей часто применяют относительный размер выборки класса k.

Для такого решения необходимо знать, является ли неодинаковое число наблюдений в различных классах отражением истинного распределения частоты наблюдения классов, или это только случайный результат процедуры выбора.

В первом случае мы положим априорные вероятности пропорциональными объемам совокупностей в выборке;

во втором – положим одинаковыми для каждой совокупности.

О различных методах ДА.

Обоснование нормального ДА

Введя расстояние Махаланобиса мы пришли на распутье НДА и КДА. Расстояние Махалонобиса в предположении о нормальности распределения х полностью совпадает с показателем степени в многомерном нормальном распределении (МНР)

Многомерная нормальная плотность распределения

Одномерная формула -

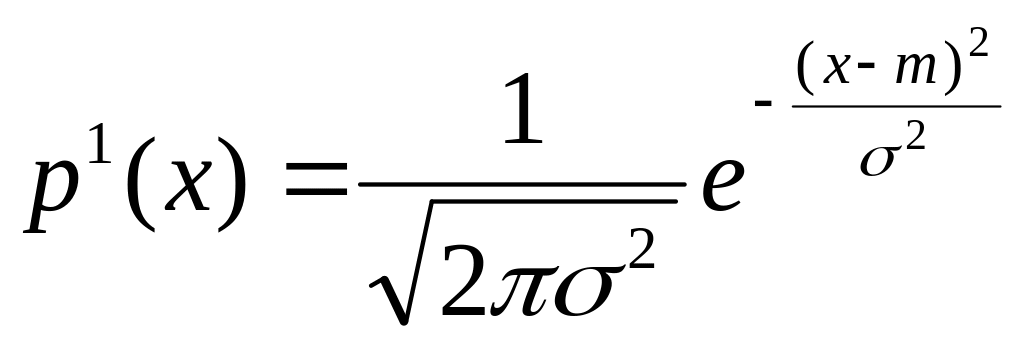
Многомерная плотность в общем виде

Видим что общий вид МНР совпадает с одномерным случаем.

Конкретное выражение дает

З десь - разм. вектора признаков х.

Как видим в показателе степени МНР стоит расстояние Махаланобиса от векторного центра распределения .

- матрица ковариаций .

Рассеяние получаемое в пространстве Х для МНСВ величины х имеют свойство попадать в одну область или кластер (рис. ).

Центр кластера определяется вектором ср. знач. , а фор­ма — ковариационной матрицей .

И з формулы плотности МРСВ следует, что точки постоянной плотности образуют гиперэллипсоиды, для ко­торых квадр. форма постоянна. Главные оси (направления ГО) гиперэллипсоидов задаются собственными векторами , а длины осей (то есть по сути дисперсии расброса) определяются собственными значениями .

Линии равного уровня то есть линии постоянства

э то линии как мы видим равного расстояния Махалонобиса до центра класса.

При линии равного расстояния Махалонобиса до центров классов делят пространство признаков на области классов линейными границами.

При разделяющими границами будут квадратичные формы

Как позже увидим рассмотренные свойства дают удобные формулы расчета

1. принадлежности к классам - линейние классификаторы и

2.вероятности класса для х -

Данные результаты - предмет многомерного НДА

Обоснование канонического ДА

При вычислении меры близости к классу сталкиваемся с проблемой

Х₁

многомерности пространства – (проклятие размерности)–

Х₁

А) Чем выше размерность, тем больше влияет механизм сглаживания различия классов (если они есть, эти различия) для каждой точки. Добавили вредный для распознавания признак и расстояния сгладились

Б) Да и попробуйте обратить матрицу ковариаций (в формуле Расстояния Махалонобиса) размером скажем 100*100 при кореллированных признаках – проблема плохой обусловленности знакома нам из РА.

Поэтому алгоритмы ДА должны быть дополнены механизмами минимизации пространства признаков в котором происходит различение классов.

Таких механизмов предложено 2:

1.Шаговые алгоритмы, оценивающие относительную эффективность различения классов в пространстве признаков Х и формирующие наилучший состав признаков из имеющихся . Идея по сути из регрессионныз шаговых алгоритмов – только надо ввести эти критерии что мы и сделаем. Подход реализуется и в рамках НДА

2 . Реализуя п.1 оптимизации пространства – получение оптимального , плюс одновременно ищется в нем путем проекции в некоторое другое , меньшее по размерности но подобранное так что-бы улучшить различающие свойства классов.

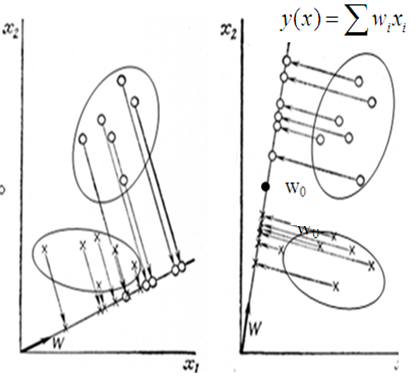
На первом рис. реализованы две разные по качеству разделения проекции из 2-мерного пространства в 1-мерное на некоторые линиии .

В первом случае не очень удачно – смешав на ней точки,

во втором случае более удачно – на ней классы разделились и видно что можно выбрать на точку – порог , который на этой прямой может служить границей, разделяющей классы.

На втором рисунке показана проекция из исходного 3-х мерного в 2-х мерное так что-бы в нем разделения классов осуществлялось наиболее просто – как видим уже на оси разделение практически получено.

Далее для механизма классификации идеология та же что и в НДА

В новом пространстве осей (переменных ) можно

- получить разделяющие (желательно линейные) поверхности делящие пространство на области классов, или

- просто вычислять уже в этом пространстве растояние Махаланобиса от точки до центра класса и отнести точку к классу по минимуму этого расстояния , или

- рассчитать вероятности классов если приняли

А) конкретную гипотезу о виде плотности распределения в классах - (как правило гипотезу о нормальности распределения) и –

Б) предположение о равенстве в классах

Приведенные интуитивные действия могут быть формализованы математически и реализованы в подходящем алгоритме если

выбрать подходящий критерий качества для положения осей проекции когда оцениваем эффективность проектирования точек и сокращения размерности пространства .для разделения классов.

Данный механизм – предмет канонического ДА.

А вот теперь поняв главную идею КДА – для того чтобы понять как

– как находяться линии проекции в КДА

было бы полезно познакомится с методом главных компонент – частью ФА, где для нахождения осей проекции применен близкий по идям подход но в упрощенном виде.

МГК нам все равно нужен в ФА, а после него проще рассказать, как искать линии наилучших проекций в КДА.

Поэтому временно отвлечемся от задачи разделения

и рассммотрим

Факторный Анализ

Метод главных компонент

МГК состоит из 2-х этапов –