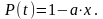Законы распределения вероятностей исходных событий

В данной реализации программного продукта распределение вероятностей исходных событий характеризуется следующими теоретическими законами:

Экспоненциальный

Экспоненциальное рас­пределение часто используют при анализе данных, зависящих от времени, когда частота появле­ния событий не изменяется.

Распределение случайной величины x называется экспоненциальным, если плотность вероятности имеет вид

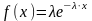
и при условии, что л=const и x≥0.

Если x - наработка до отказа, то величина л называется интенсивностью отказов.

График плотности распределения f(x) (см. рис. 1) представляет собой спадающую экспоненту, у которой при f(x) = л, а при x→∞ f(x)→0.

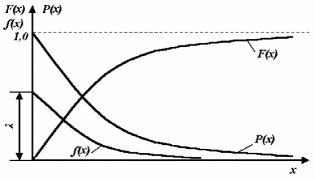
Рис. 1. Графики плотности вероятности f(x), функции F(x) и вероятности безотказной работы P(x)

Функция распределения находится по уравнению:

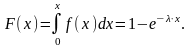
Если x - наработка до отказа, то F(x) - это вероятность отказа до момента x.

Чем больше x, тем больше вероятность отказа. График функции распределения F(x) представляет собой нарастающую экспоненту, у которой при x = 0 F(0) = 0, а при x→∞ F(∞)→1.

Вероятность безотказной работы до момента x

График функции безотказной работы P(x) представляет собой спадающую экспоненту, у которой при x = 0 P(0) = 1, а при x→∞ Р(∞)→0.

Нормальный

Нормальное распределение (или распределение Гаусса) является наиболее известным двухпараметрическим распределением. Все нормальные распределения симметричны. Двумя параметрами этого распределения являются M и у т. е. его среднее значение и стан­дартное отклонение.

Нормальные распределения часто используют для описания характеристик оборудования, которое имеет возрастающую со вре­менем частоту отказов и занимает особое место в теории вероятностей и в теории надежности.

Нормальным распределением называется распределение вероятности непрерывной случайной величины, которая может принимать как отрицательные, так и положительные значения во всем диапазоне возможных значений от -∞ до +∞.

Плотность вероятности имеет вид:

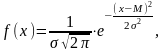
где у - положительная величина, М - любая положительная, отрицательная или нуль.

Кривая плотности (см. рис. 2) симметрична относительно центра, так как (х - М)², и достигает максимума при х = М.

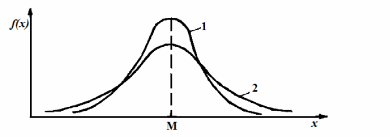
Рис. 2. Графики плотности вероятности нормального распределения у1<у2; М1=М2=М

Значит, математическое ожидание – это среднее значение случайной величины, а у – среднеквадратическое отклонение, определяет величину рассеивания вокруг центра распределения.

Функция распределения находится по уравнению:

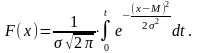
Вероятность безотказной работы до момента x

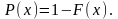
Логарифм-нормальный

Логарифмически-нормальное распределение подобно нормаль­ному распределению, за исключением того, что вместо самих вели­чин принимают нормально распределенные логарифмы значений случайной переменной. Таким образом, все значения положительные, распределения сдвинуты вправо, а степень смещения зависит от у.

Логарифмически-нормальные распределения часто встречаются при обработке данных усталостных испытаний, данных по обслу­живанию и ремонту (по срокам ремонта), а также по отказам и ре­монтам химико-технологического оборудования.

Графики плотности вероятности этого распределения приведены на рис. 3.

Рис 3. График плотности вероятности логнормального распределения:

1 – для у1, 2 – для у2

Вейбулла

Это распределение непрерывной случайной величины, которая может принимать только положительные значения с плотностью вероятности:

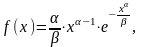
функция распределения:

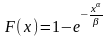
и вероятность безотказной работы:

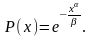
x - величина переменная. Постоянные параметры б и в носят название: б - параметр формы и в - параметр масштаба. В экспоненциальном распределении параметр л - один, здесь - два. Значит, это распределение более сложное. Оно служит для расчетов долговечности технических объектов, для описания распределения сроков службы различных элементов машин. Оно хорошо описывает отказы механических систем в начальный период эксплуатации и отказы из-за хрупких и усталостных разрушений. У шарикоподшипников наработка до отказа подчиняется этому распределению с показателем б = 1,4. У электронных ламп - б = 1,4 - 1,6.

При б = 1 получим экспоненциальное распределение.

Параметры распределения б и в можно найти по формулам:

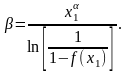
Графики f(x) распределения Вейбулла при различных значениях параметра б приведены на рис. 4.

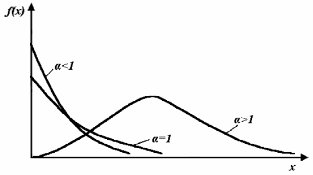
Рис. 4. Графики плотности распределения Вейбулла

Равномерный

Это распределение непрерывной случайной величины, которая может принимать только положительные значения.

Функция распределения имеет следующий вид:

Произвольный (вероятность жестко указывается пользователем)

В данном случае вероятность жестко указывается в формуле и в итоге мы получаем следующие формулы. Для определения плотности вероятности:

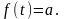
Функция распределения имеет следующий вид:

И вероятность безотказной работы: