8. Поняття двоїстої.

Теорія двоїстості – центральна частина лінійного програмування. Дослідження двоїстості дало можливість отримати важливі теоретичні (розробити ефективні методи розв’язування ЗЛП, проаналізувати та оцінити чутливість моделей лінійного програмування) і практичні (дати економічне тлумачення отриманого розв’язку, розкрити нові закономірності та співвідношення, властиві досліджуваній проблемі) результати.

На початковій стадії дослідження задач лінійного програмування виявили, що кожній ЗЛП відповідає інша, цілком визначена ЗЛП, тобто ці задачі взаємопов’язані: якщо вихідною вважати другу, то їй відповідатиме перша. Крім того, взаємозв’язок настільки тісний, що в ході розв'язування одної з них фактично розв’язується й інша задача. Ця пара була названа двоїстою (спряженою) парою задач.

Економ. інтерпретація двоїстої задачі: якими мають бути ціни одиниці ресурсів, щоб при заданих обсягах ресурсів (b_i) і прибутку від реалізації одиниці продукції (с_j) мінімізувати загальну вартість ресурсів; у_і називаються оцінками, або обліковими, неявними цінами. Ці оцінки (ціни) - відносні, оскільки одні й ті самі ресурси для різних підприємств мають різну цінність, а оцінки ресурсів для того самого підприємства також змінюються зі зміною обсягів ресурсів. Відносність оцінок обумовлена ще й тим, що вони виражаються в одиницях вартості продукції, що випускається. Аналізуючи математичні моделі двоїстих пар задач можна встановити зв’язок між математичними моделями задач і вказати етапи формальної побудови математичної моделі однієї із задач за відомою моделлю іншої. системи обмежень вихідної задачі;

Матем. модель задачі. Знайти такі х_j, які забезпечують максимум функції

Z = c₁х₁ + с₂х₂ + … + с_nx_n (max)

і задовільняють обмеження

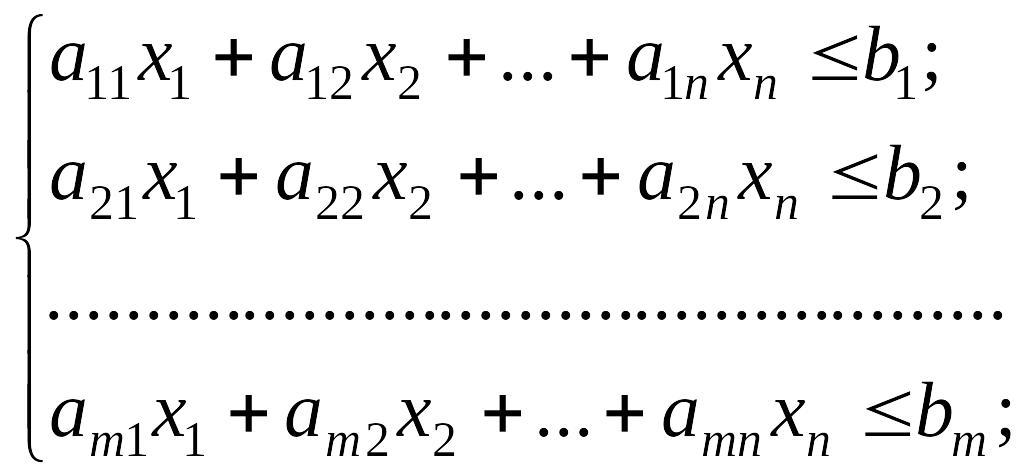
Економічна інтерпретація цієї задачі: скільки та якої продукції треба виробити, щоб при заданих обсягах ресурсів, які витрачаються, максимізувати прибуток.

Нехай у_і - ціна одиниці ресурсу і-го виду, тоді вартість усіх ресурсів

f = b₁y₁ + b₂y₂ + ... + b_my_m.

Прибуток від продажу ресурсів, потрібних для випуску одиниці j-го виробу, має бути не меншим за прибуток від реалізації готового виробу:

a_1jy₁ + a_2jy₂ + … +a_mjy_m ³ c_j.

Отже, двоїсту задачу можна сформулювати так. Знаючи у₁, у₂, ..., у_т, які надають мінімуму функції

f = b₁y₁ + b₂y₂ + ... + b_my_m (min)

і задовольняють обмеження

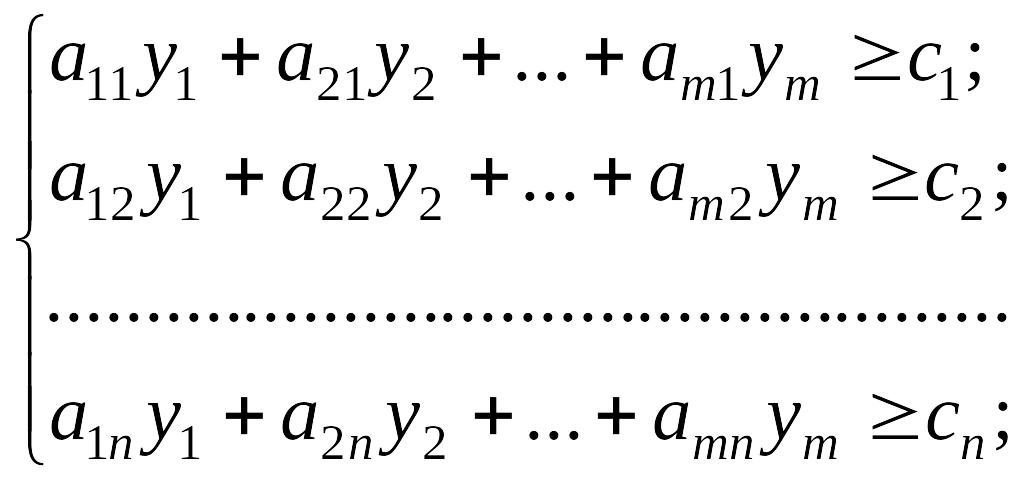
Економічна інтерпретація двоїстої задачі: якими мають бути ціни одиниці ресурсів, щоб при заданих обсягах ресурсів (b_i) і прибутку від реалізації одиниці продукції (с_j) мінімізувати загальну вартість ресурсів;

15. Виробнича функція. Властивості.

ВФ-це відношення між б-я набором ФВ, та макс можливим обсягом прод-ії, виробленим за доп. цього набору факторів.

ВФ є екон.-стат. моделлю процесу вироб-тва прод-ії в даній економ. системі й виражає закономірну кількісну залежність між показниками, що характ. обсяги ресурсів і випуску продукції.

ВФ– це ф-я, де аргументи – ресурси виробництва, а значення ф-ії – кількість виробленої продукції..

В загальному вигляді виробнича функція має вигляд: y=f(x₁;x₂;…;x_n), де x₁;x₂;…;x_n - об’єми ресурсів, а y - кількість виготовленої продукції.

Частіше застосовують ВФ від 2 змінних, які найб. впливають на результат виробництва. Результат виробництва вимірюється одним вартісним показником (показником валової продукції). Виробничі ресурси характер. 2 показниками, а саме, витратами основного капіталу та праці: V=f(K;L). ВФповинна відповідати наступним вимогам.

1) Якщо K>0 і L>0, то f (K;L)>0. З екон. точки зору це означає, що взаємодія трудових ресурсів і вироб. фондів приводить до виробництва продукту.

2) Якщо K*L=0 , то f(K;L)=0. Це означає необхідність для процесу виробництва наявності обох ресурсів.

3) Позитивність частинних похідних:

.

Це віддзеркалює факт зростання обсягу виробництва при збільшенні використання одного з ресурсів при незмінному споживанні іншого. Будь-яке підпр-тво досягає у своїй діяльності такої межі, за якою продуктивність додаткових вкладень в один ресурс (при незмінному використанні інших) спадає в порівнянні з віддачею від попередніх.

4) Для частинних похідних другого порядку повинні виконуватися вимоги:

будь-яке підприємство досягає у своїй діяльності такої межі, за якою продуктивність додаткових вкладень в один ресурс (при незмінному використанні інших) спадає в порівнянні з віддачею від попередніх..

5) Виробнича функція повинна бути однорідною, що означає, що при збільшенні використання всіх ресурсів у λ раз, обсяг продукції зростає в λⁿ раз.

9 Гамно

Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею.

Зв’язок між оптимальними розв’язками прямої та двоїстої задач встановлюють леми та теореми двоїстості.

(достатня умова оптимальності). Якщо та — допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність

то X*, Y* — оптимальні розв’язки відповідних задач.

Лемма 1.1. Якщо X — деякий план вихідної задачі (1) — (3), а В — довільний план двоїстої задачі (4), (5), те значення цільової функції вихідної задачі при плані X завжди не перевершує значення цільової функції двоїстої задачі при плані Y, тобто F(X)<= F*(Y)

Лемма 1.2. Якщо F(X*) = F*(Y*) для деяких планів X* і Y* задач (1) — (3) і (4), (5), те X* — оптимальний план вихідної задачі, a Y* — оптимальний план двоїстої задачі

Теорема 1. (перша теорема подвійності) Якщо одна з пари двоїстих задач (1) — (3) чи (4), (5) має оптимальний план, те й інша має оптимальний план і значення цільових функцій задач при їхніх оптимальних планах рівні між собою, тобто .Якщо ж цільова функція однієї з пари двоїстих задач не обмежена (для вихідної (1) — (3) —зверху, для двоїстої (4), (5) — знизу), то інша задача взагалі не має планів.

Теорема 2. (друга теорема подвійності). План задачі (1) — (3) і план задачі (4), (5) є оптимальними планами цих задач тоді і тільки тоді, коли для будь-якого виконується рівність