2.3.Содержательная декомпозиция базы знаний проектируемой интеллектуальной системы

База знаний разрабатываемой интеллектуальной справочной системы декомпозируется следующим образом:

1. Логика высказываний

2. Логика предикатов

3. SCL

На данном этапе в прототипе реализованы только частично 1, 2, 3 разделы.

2.4.Исходные тексты базы знаний прототипа интеллектуальной системы

Примеры статей на SCg

Рисунок 2.1- Ассоциативное исчисление или система Туэ

Рисунок 2.2 - Теормема Геделя(Вторая) Рисунок 2.3 - Дизъюнкт

Рисунок 2.4 - Логическая функция

Рисунок 2.5 – Отношение нестрогого порядка

Рисунок 2.6 – Опр(Ассоциативное исчисление или система Туэ)

Рисунок 2.7 – Опр.(Дизъюнкт)

Рисунок 2.8 – Опр(Система подстановок или полусистема Туэ)

Рисунок 2.9 - Эквивалентное соотношение

Рисунок 2.10 – Чистое исчисление предикатов

Рисунок 2.11 – Хорновский дизъюнкт

Рисунок 2.12 - Опр.(Теорема Геделя(Первая))

Рисунок 2.13 Опр.(Теорема Геделя(Вторая))

Рисунок 2.14 – Опр.(Теорема Поста о нормальной форме) Рисунок 2.15 - Опр.(формально-непротиворечивая теория) Рисунок 2.16 – Опр.(Отношение строгого порядка)

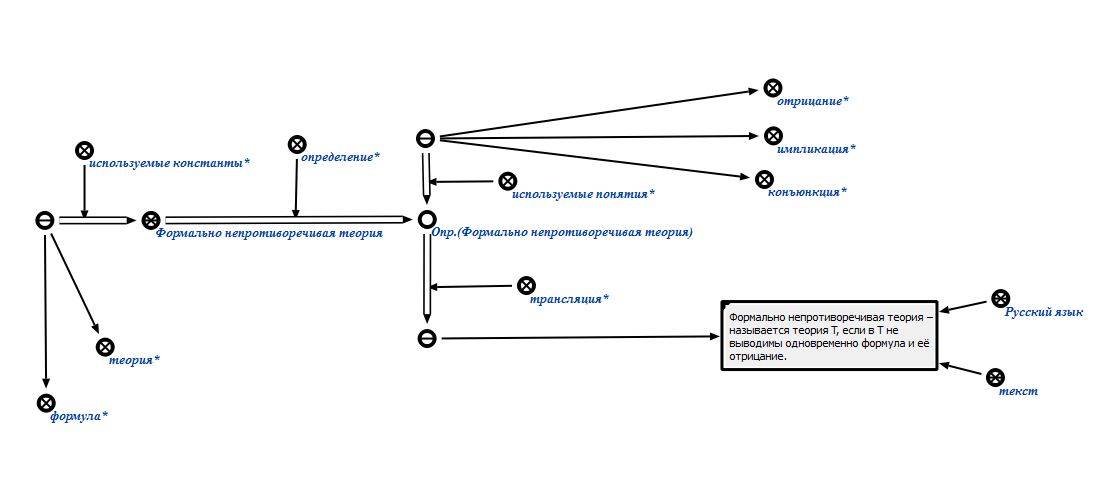Рисунок 2.17 – Теорема Геделя (Первая) Рисунок 2.18 – Система подстановок или полусистема Туэ Рисунок 2.19 – Тождественно истинное высказывание Рисунок 2.20 – Формально непротиворечивая теория

Рисунок 2.21 – Опр.(Хорновский Дизъюнкт)

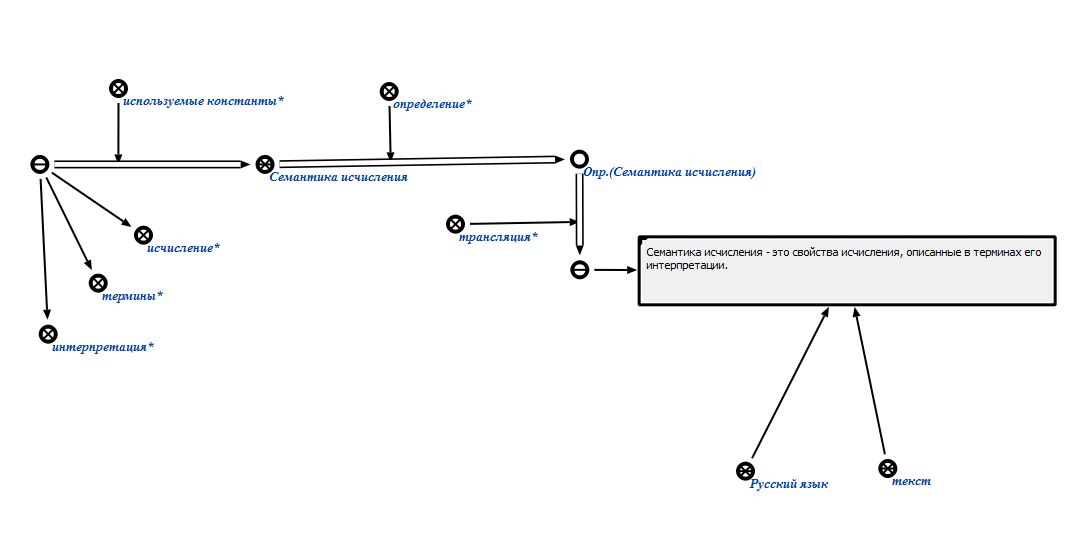
Рисунок 2.22 – Семантика исчисления

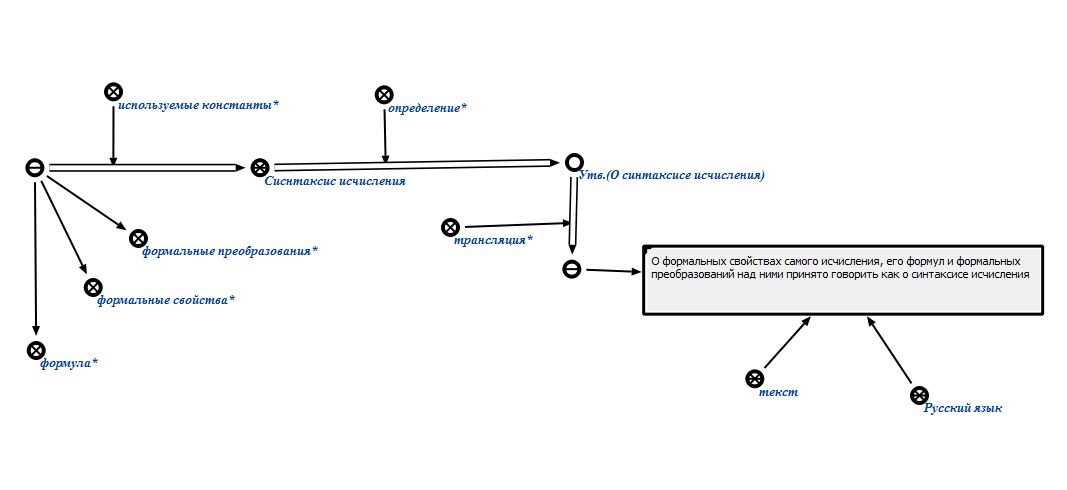
Рисунок 2.23 – Синтаксис исчисления

Рисунок 2.24 – Субъект

Рисунок 2.25 – Теорема Поста о нормальной форме

Для примера приведём несколько статей на SCn:

• Модус Darii

Утв.(модус Darii)

≗ [Если всякий термин M есть термин P иесли всякий термин S есть термин M, то всякий термин S есть термин P.]

≗ [Для любых _S, _M, _P имеет место

импликация:

• если имеет место

коньюнкция:

•• для любых _x имеет место

импликация:

••• если _x∈_M,

••• то _x∈_P,

•• для любых _y имеет место

импликация:

••• если _y∈_S,

••• то _ y∈_M,

• то существует _z,

для которого имеет место

импликация:

•• если _z∈_S,

•• то отрицание: _z∈_P.]

∈ Предметная область Логика предикатов в роли утверждения_

• Модус Ponens

= правило заключений ∈ модус

– Отношения, области определения которых являются надмножеством описываемого множества и связки которых, в общем случае, связывают элементы описываемого множества с другими объектами:

• посылка*

• заключение*

Утв.(модус Ponens)

≗ [если A и A→B — выводимые формулы, то B также выводима.]

≗ [Для любых _A, _B - формулы,_Vf – выводимые формулы,_F – выводима имеет место

импликация:

• если имеет место

коньюнкция:

••_Vf∈_A

•• имеет место

импликация:

••• если _Vf∈_A,

••• то _Vf∈_B,

• то _F∈_B.]

∈ Предметная область Логика предикатов в роли утверждения_

Формальная теория

= Класс формальных теорий

= Множество формальных теорий

= Понятие формальной теории

– Определение:

• Опр.(Формальная теория)

≗ [ Формальная теория - это множество логических закономерностей, описывающих предметную область. ]