Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Г.Н. Миренкова, С.В. Неделько, В.М. Неделько, Т.В. Тренёва

ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Утверждено Редакционно-издательским советом университета в качестве учебно-методического пособия

НОВОСИБИРСК

2008

УДК 519.22(075.8)

О-753

Рецензенты: д-р техн. наук, профессор Г.С. Лбов; канд. физ.-мат. наук, доцент А.П. Ковалевский

Работа подготовлена кафедрами высшей математики и ПС и БД для студентов II курса РЭФ и ФПМИ

О -753         Основы математической статистики : учебно-метод. пособие / Г.Н. Миренкова, С.В. Неделько, В.М. Неделько, Т.В. Тренёва.  Новосибирск : Изд-во НГТУ, 2008.  36 с.

ISBN 978-5-7782-0929-9

Пособие содержит изложение методов решения ряда базовых задач математической статистики, а также задания для самостоятельной работы.

УДК 519.22(075.8)

ISBN 978-5-7782-0929-9 © Миренкова Г.Н., Неделько С.В.,

Неделько В.М., Тренёва Т.В., 2008 © Hовосибиpский государственный технический университет, 2008   

О главление

1. Основные понятия из теории вероятностей и математической статистики 4

2. Эмпирическая функция распределения. Гистограмма 6

3. Точечные оценки для моментов 10

4. Доверительные интервалы для моментов. Доверительная вероятность 12

5. Оценивание параметров. Метод моментов 16

6. Критерии согласия 20

7. Задания практических работ 24

Приложение 1 29

Приложение 2 30

Приложение 3 32

Приложение 4 34

Литература 36

Коллектив авторов 36

1. Основные понятия из теории вероятностей и математической статистики

В настоящем разделе вводятся основные используемые понятия из теории вероятностей. Из-за краткости изложения приведенные определения не предназначены для изучения соответствующих понятий, а включены лишь как справочный материал.

Для чтения пособия следует иметь знакомство с теорией вероятностей и математической статистики в рамках начальных курсов, например с работами [1, 3, 4].

Допустимо, если при первом прочтении часть материала данного раздела останется непонятной. Это не препятствует изучению последующих разделов.

Базовым понятием теории вероятностей является вероятностное пространство, которое включает множество элементарных исходов Ω, σ-алгебру Λ событий и вероятностную меру P.

Множеством элементарных исходов может быть любое конечное, счетное или континуальное множество Ω.

Функция называется вероятностной мерой, если:

1) ;

2) , ;

3) для попарно несовместных (непересекающихся) событий

.

Случайной величиной называется измеримая функция . Измеримость здесь означает существование функции распределения .

При пользовании настоящим пособием читатель может под случайной величиной понимать просто некоторую переменную X, для которой определена функция распределения. При этом под функцией распределения достаточно понимать некоторую функцию F(x), такую что:

1) ;

2) ;

3) ;

4) .

Величина есть вероятность¹ попадания X в интервал   .

Для системы случайных величин определена совместная функция распределения .

В математической статистике важную роль играют независимые случайные величины. Случайные величины называются независимыми, если их совместная функция распределения удовлетворяет условию .

Под выборкой² будем понимать набор значений , полученных как n независимых реализаций случайной величины X. Число n называется объемом выборки.

Например, случайной величиной может являться измеряемое значение некоторой физической величины, тогда выборкой будут результаты n независимых измерений.

Задачи математической статистики заключаются в восстановлении той или иной информации о случайной величине по выборке. Основные задачи следующие:

1) восстановление закона распределения непараметрическими методами;

2) оценивание параметров распределения (параметрические методы);

3) проверка состоятельности гипотезы о законе распределения.

Непараметрический подход включает такие способы восстановления распределения, как построение эмпирической функции распределения и гистограммы, а также множество методов (потенциальных функций и др.), не рассматриваемых в настоящем пособии.

Представителями параметрических методов являются методы моментов и максимального правдоподобия для оценки параметров распределения. Некоторые другие методы читатель может найти в литературе.

2. Эмпирическая функция распределения. Гистограмма

Эмпирическая функция распределения

Эмпирической функцией распределения называется функция , где – количество значений из выборки , меньших x (т.е. число выборочных точек, расположенных на числовой оси левее заданного числа x).

Эмпирическая функция распределения определяет частоту события, в то время как теоретическая функция распределения определяет вероятность этого события.

Эмпирическая функция распределения может считаться приближением (оценкой) функции распределения . Ее значения, так же как и значения , изменяются от нуля до единицы.

По теореме Бернулли при большом числе испытаний частота события X <x сходится по вероятности к вероятности этого события. Следовательно, сходится по вероятности к неизвестной теоретической функции распределения. Построение эмпирической функции распределения является простейшим методом обработки наблюдаемых значений случайной величины.

Для построения графика этой функции достаточно изобразить выборочные значения на числовой оси 0x и нарисовать ступенчатую функцию, возрастающую в каждой точке выборки на . Этот способ применим, когда все выборочные точки различны. Если некоторое значение встречается в выборке r раз, то скачок в этой точке увеличивается также в r раз.

Стрелки на «ступенях» отражают тот факт, что функция в точках разрыва непрерывна слева.

На рис. 1 изображена эмпирическая функция распределения для выборки 1,8; 2; 3,3; 2,6; 1,3; –4; 0,5; 0,7; –0,7; 5,1; 5,7; 2 объема 12 (задание 1 практической работы 1, вариант 0 таблицы 4).

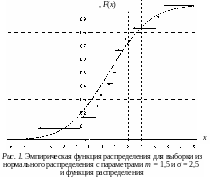
Во всех точках выборки, кроме точки 2, возрастает на 1/12. В точку 2 попали две выборочные точки, поэтому скачок в ней вдвое больше, чем в точках, вошедших в выборку однократно, и равен 2/12 = 1/6.

Для сравнения на рис. 1 приведена теоретическая функция распределения нормально распределенной случайной величины с математическим ожиданием m = 1,5 и среднеквадратическим (стандартным) отклонением σ = 2,5 (параметры распределения указаны в последних колонках таблицы). Выборка является реализацией этой случайной величины.

Гистограмма

Гистограмма наблюдений также является инструментом восстановления распределения случайной величины по выборке. При этом число наблюдений должно быть достаточно велико, не менее пятидесяти выборочных точек. Если число наблюдений невелико, то лучше использовать иные методы обработки данных, например, построить эмпирическую функцию распределения.

В выборке объема n находятся наименьшее и наибольшее значения, пусть это будут и соответственно. Весь диапазон наблюдаемых значений разбивается на несколько интервалов (разрядов). Интервалы могут быть как одинаковыми, так и различными. Далее будут рассматриваться одинаковые интервалы длиной где l есть число интервалов. Для определенности считаем, что левые границы строго включены в интервалы, а правые  нестрого. Если значение из выборки совпадает с левой границей, то оно входит в данный разряд, если совпадает с правой границей, то относится к следующему интервалу. Самая правая граница включается в последний разряд.

Далее подсчитывается количество значений выборки, попавшее в i-й разряд. Эмпирическая частота для интервала находится по формуле .

Сумма частот должна равняться единице. Рассматриваются также относительные частоты . Полученные данные заносятся в таблицу, называемую статистическим рядом.

Построим статистический ряд для данных (табл. 5) варианта 0, практическая работа 2. В отличие от практической работы 1 выборка объема 100 здесь задается не конкретными значениями точек, а интервально. Весь диапазон значений от до предполагается уже разбитым на l=10 разрядов длиной 4. В табл. 5 перечислены через точку с запятой количества выборочных точек в каждом интервале.

Таблица 1

i	1	2	3	4	5	6	7	8	9	10
	[10;14)	[14;18)	[18;22)	[22;26)	[26;30)	[30;34)	[34;38)	[38;42)	[42;46)	[46;50]
	6	7	11	17	19	18	13	5	3	1
	0,06	0,07	0,11	0,17	0,19	0,18	0,13	0,05	0,03	0,01
	0,015	0,0175	0,0275	0,0425	0,0475	0,045	0,0325	0,0125	0,0075	0,0025

В табл. 1 приведен построенный статистический ряд. Данные из табл. 1 графически представляются в виде гистограммы. Гистограмма есть ступенчатая фигура из прямоугольников с основаниями на . Высоты прямоугольников равны относительным частотам . Площадь гистограммы равна единице. Иначе говоря, гистограмма является кусочно-постоянной аппроксимацией плотности вероятности. На рис. 2 совместно изображены гистограмма и плотность вероятности для случайной величины, реализациями которой является данная выборка (нормальная плотность с параметрами m = 29; σ = 9).