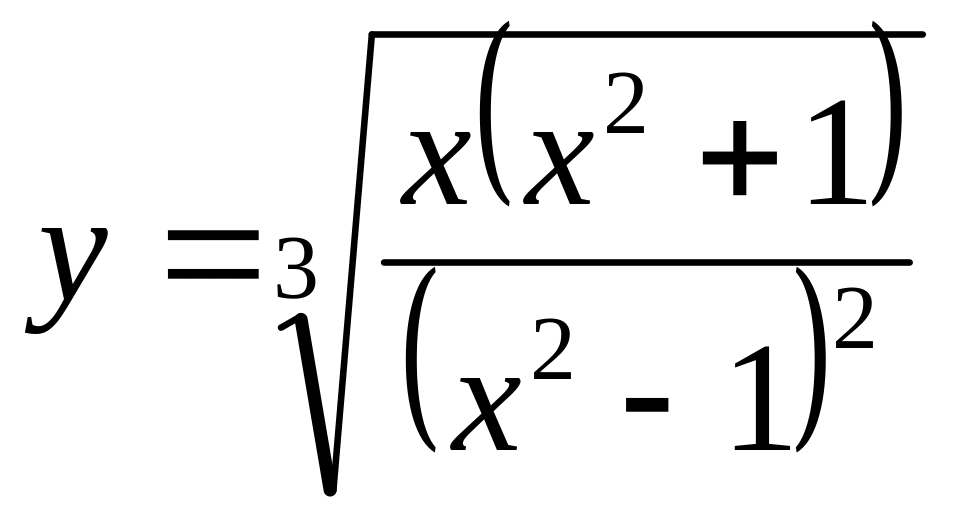- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •27 Вариант
- •28 Вариант
- •29 Вариант
- •30 Вариант
5 Вариант
1. Найти
для функции
![]() .
.
2. Пользуясь таблицей производных, найти производные следующих функций:
|
|
|
|
|
|
|
|
|
|
|
|
3. Найти от функций, заданных неявно:
|
|
4. Найти
от функции
![]()
5. Найти
и y''xx
от функции, заданной параметрически:
![]()
6. Под каким углом пересекаются
кривые
![]() и
и
![]() ?
?
7. Найти приближенное значение
![]()
8.
![]() .
Найти
.
.
Найти
.
9. Показать, что теорема Лагранжа на
отрезке
![]() неприменима к функции
неприменима к функции
![]() Пояснить это утверждение графически.
Пояснить это утверждение графически.
10. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции f (x) = ex, вычислить значение ea при а = 0,21, с точностью до 0,001.
11.
Найти наибольшее и наименьшее значения
функции f (x)
=
![]() на
отрезке
на
отрезке
![]() .
.
12. Найти радиус основания и высоту конуса наименьшего объема, описанного около шара радиуса R.
13. Исследовать методами дифференциального исчисления функцию у = f (x) и, используя результаты исследования, построить график:
а)
![]() б)
б)
![]() .
.
14. Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t0.
![]()
15. Дана функция z
=
![]() .
Показать, что F =
.
Показать, что F =
![]()
16. Дана функция z = x2 + 2xy + 3y 2и две точки А (2; 1) и В (1,96; 1,04). Требуется: 1) вычислить значение z1 в точке В; 2) вычислить приближенное значение z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности z = F (x; y) в точке С(2; 1; zА).
17. Дана функция z = 5x2 + 6xy, точка А(2; 1) и вектор (1; 2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .
6 Вариант
1. Найти
для функции
![]() .
.
2. Пользуясь таблицей производных, найти производные следующих функций:
|
|
|
|
|
|
|
|
|
|
|
|
3. Найти и y''xx от функций, заданных неявно:
|
|
4. Найти
от функции
![]()
5. Найти
от функции, заданной параметрически:
![]()
6. Написать уравнение касательной
к кривой
![]() в точке пересечения с осью
в точке пересечения с осью
![]()
7. Найти приближенное значение
![]()
8.
![]() Найти
.
Найти
.
9. Функция
![]() принимает равные значения на концах
интервала
принимает равные значения на концах
интервала
![]() Убедиться в том, что производная от этой
функции нигде в интервале
Убедиться в том, что производная от этой
функции нигде в интервале
![]() в ноль не обращается и объяснить такое
уклонение от теоремы Ролля.
в ноль не обращается и объяснить такое
уклонение от теоремы Ролля.
10. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции f (x) = ex, вычислить значение ea при a=0,55 с точностью до 0,001.
11.
Найти наибольшее и наименьшее значения
функции f (x)
=
![]() на
отрезке
на
отрезке
![]() .
.
12. При каких линейных размерах закрытая цилиндрическая банка данной вместимости, будет иметь наименьшую полную поверхность?
13. Исследовать методами дифференциального исчисления функцию у = f (x) и, используя результаты исследования, построить график:
а)
![]() б)
б)
![]() .
.
14. Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t0.
![]()
15. Дана функция z
=
![]() .
Показать, что F =
.
Показать, что F =
![]()
16. Дана функция z = x2 + y2 + 2x + y – 1 и две точки А (2; 4) и В (1,98; 9,91). Требуется: 1) вычислить значение z1 в точке В; 2) вычислить приближенное значение z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности z = F (x; y) в точке С (2; 4; zА).
17. Дана функция z = arctg (xy2), точка А (2; 3) и вектор (4; -3). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .