Потенциальное течение жидкости.
Потенциа́льное тече́ние — безвихревое движение жидкости или газа, при котором деформация и перемещение малого объема жидкости происходит без вращения (вихря). При потенциальном течении скорость жидкости может быть представлена следующим образом:
где — некоторая скалярная функция, называемая потенциалом скорости течения. Движение реальных жидкостей будет потенциальным в тех областях, где действие сил вязкости ничтожно мало по сравнению с действием сил давления и в которых нет завихрений, образовавшихся за счет срыва со стенок пограничного слоя или за счет неравномерного нагревания. Необходимым и достаточным условием потенциальности течения являются равенства:
Вихревое течение жидкости.
Вихревое
движение — движение жидкости
или газа,
при котором мгновенная скорость вращения
элементарных объёмов среды не равна
нулю. Количественной мерой завихренности
служит вектор 
,
где v — скорость жидкости; ω
называют вектором
вихря или
просто завихренностью.
Движение называется безвихревымили потенциальным,
если ω = 0, в противном случае имеет место
вихревое движение.
Векторное поле вихря удобно характеризовать некоторыми геометрическими образами. Вихревой линией называется линия, касательная к которой в каждой точке направлена по вектору вихря; совокупность вихревых линий, проходящих через замкнутую кривую, образует вихревую трубку. Поток вектора вихря через любое сечение вихревой трубки одинаков. Он называется интенсивностью вихревой трубки и равен циркуляции скорости по произвольному контуру C, однократно охватывающему вихревую трубку[1].
Вывод уравнения неразрывности.
Уравнение неразрывности либо сплошности выражает один из фундаментальных законов природы - закон сохранения массы применительно к жидкой среде.
- орт внешней нормали, а
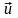- вектор скорости. Через выделенный
элемент dS в единицу времени внутрь
объема проникает масса жидкости
.
Рис. 4.2
.
С другой стороны, приток жидкости в объем приводит к изменению ее массы. При этом, поскольку выделенный объем является постоянным, изменение массы может происходить только за счет изменения ее плотности. Скорость изменения массы можно представить как
,
либо
с учетом того, что
,
можно записать
.
Очевидно, что изменение массы внутри объема должно быть равно массе, поступившей в него извне, т.е.
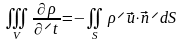
Применяя преобразование Гаусса-Остроградского, получим:
,
либо
.
Равенство нулю интеграла возможно лишь при условии
. (4.3)
Это и есть уравнение неразрывности. Поскольку при выводе его не делалось никаких ограничений, то оно справедливо как для установившегося, так и для неустановившегося движений сжимаемой и несжимаемой жидкости. Уравнение (4.3) относится к числу фундаментальных уравнений механики жидкости.
Уравнение движения в напряжениях.
Выделим произвольный объем жидкости W, ограниченный поверхностью S, и запишем для него закон изменения количества движения: производная по времени от главного вектора количества движения системы равна главному вектору приложенных к ней внешних сил, или
..
Преобразуем данное уравнение:
поменяем местами знаки дифференцирования и интегрирования в левой части уравнения и распишем дифференциал произведения. Получим
..
Так как в процессе движения жидкости ее масса не меняется, то на основании уравнения неразрывности последнее слагаемое обращается в нуль;
с помощью формулы Остроградского-Гауса интеграл по поверхности от потока вектора можно преобразовать в интеграл по объему от дивергенции этого же вектора, т.е.
..
Подставляя в уравнение, описывающее закон изменения количества движения, преобразованные выражения, после выполнения элементарных операций получим
..
Данное выражение справедливо при равенстве нулю подынтегрального выражения, следовательно
. . (1.5.1)
Полученное выражение представляет собой векторную форму уравнения движения жидкости в напряжениях. В проекциях на оси координат оно имеет вид:
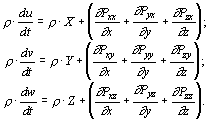(1.5.2)