6.Гармоническая линеаризация.

Метод гармонической линеаризации является приближенным методом исследования НСАР. Основу этого метода составляют следующие положения.

Пусть имеется нелинейное звено с характеристикой y = F(x). Подадим на вход этого звена гармонический сигнал x = A∙sin ωt. На выходе получим y = F(A∙sin ωt). Этот периодический выходной сигнал можно разложить в ряд Фурье.

Предположим, что наша система обладает тем свойством, что величина амплитудной характеристики на частотах высших гармоник значительно меньше, чем для первой: |Wл(jnω)| << |Wл(jω)|, где n = 2, 3, …

Это свойство называется свойством фильтра линейной части системы. Значит, в силу резонансных и фильтрующих свойств линейной части, на выходе НЭ для расчета периодических режимов можно учитывать только основную, первую гармонику, получим x = A∙sin ωt.

Проведем гармоническую линеаризацию нелинейного элемента:

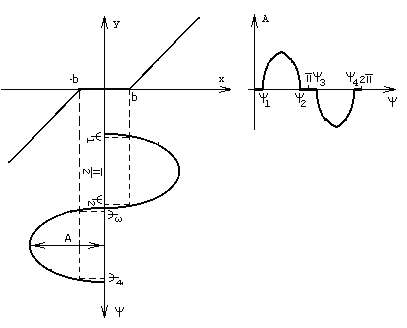
Найдем q(A) и b(A):

В силу симметрии функций sin и НЭ относительно центра координат будем рассматривать интеграл на четверти периода (от 0 до ):

то

то

На участке F(Asinψ)=0

На участке F(Asinψ)=

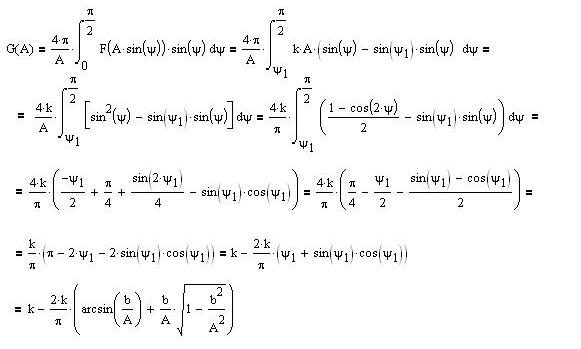
7.Расчет нсар частотным методом.

Периодическое решение линеаризованной системы x = A∙sinωt получается при наличии в характеристическом уравнении замкнутой системы пары чисто мнимых корней. А это по критерию Найквиста соответствует прохождению W(jω) через точку –1. Следовательно, периодическое решение определяется неравенством Wл(jω) ∙ Wнэ(A) = –1

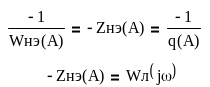
1. Рассчитаем систему без запаздывания т.е. при τ = 0 с:

Д ля этого найдем частоту ω₀ при котором ФЧХ ЛЧ будет равна –π

– ФЧХ ЛЧ

б

Это уравнение имеет корень ,но это на практике не реализуемо, следовательно, нет периодического режима в системе.

Это можно видеть на рис.4.

2. Рассчитаем систему при τ = 2 с:

Д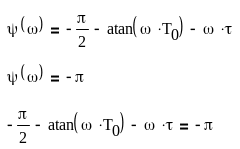 ля этого найдем частоту ω₀ , при котором ФЧХ ЛЧ будет равна –π

– ФЧХ ЛЧ

Решением данного уравнения будет частота ω₀ = 0.128 с^-1

Приравняем –Z_НЭ(A_П) = A(ω₀)

где – АЧХ ЛЧ

уравнение не имеет решения, значит периодического режима нет.

Графики АФХ линейной части и нелинейного элемента:

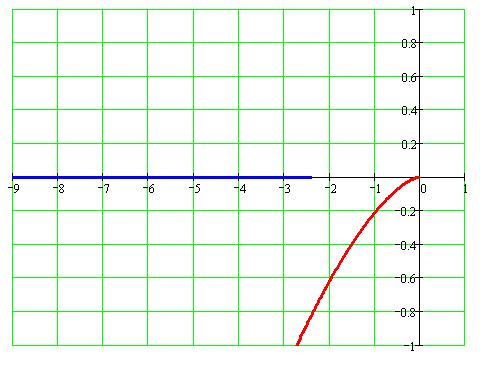
АФХ линейной части и нелинейного элемента без запаздывания

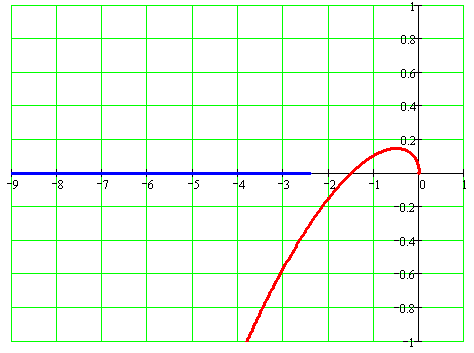
АФХ линейной части и нелинейного элемента с запаздыванием ( )

Найдём значение k_gr , при котором у нас будет периодический режим:

ω₀ = 0.128 с^-1

амплитуда на данной частоте будет равна A(ω₀)=1.47663

т.е.

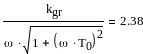
тогда получим .При k>=k_gr в системе будет иметь место периодический режим.

8.Построение диаграммы качества.

Для построения диаграммы качества будем рассматривать колебательный переходный процесс в системе как собственные колебания системы при отсутствии внешних воздействий. Если выполнена гармоническая линеаризация нелинейного элемента, то переходный процесс мы будем искать в виде:

Будем считать переходные колебания близкими к синусоидальным, полагая, однако, что показатели затухания ξ и ω медленно изменяются с изменением амплитуды колебаний a в ходе процесса. Сама амплитуда а(t) может меняться быстро вплоть до затухания за один – два периода. Тогда решение вместо (9) надо искать в виде:

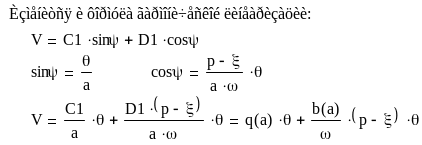
коэффициенты q(a) и b(a) вычисляются аналогично гармонической линеаризации НЭ.

Для построения диаграммы качества используем:

подставив вместо Q знаменатель передаточной функции ЛЧ, а вместо R его числитель и, выделив мнимую и действительную части, получим:

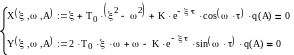
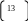
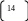
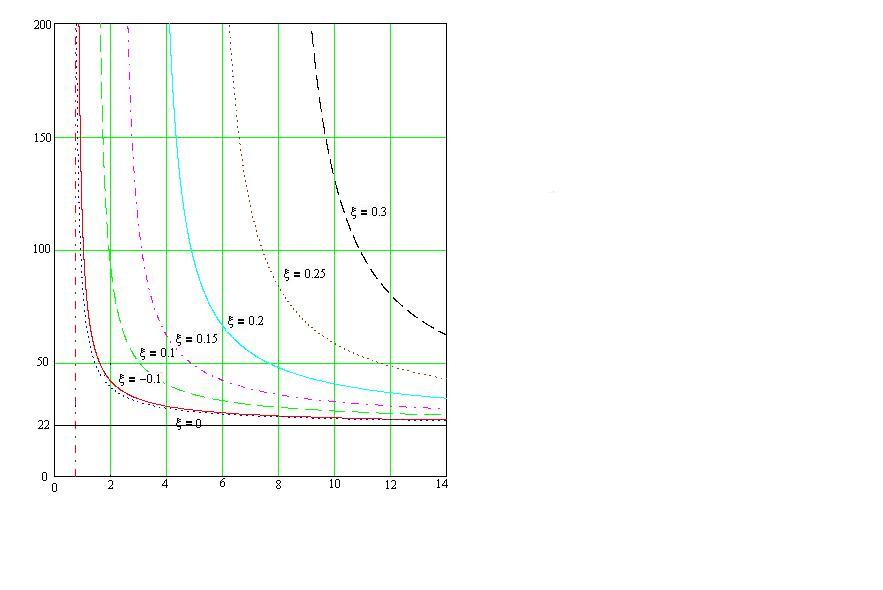
Из (14) выделим ω от ξ, K и подставим в (14). В итоге получим:

Подставляя вместо ξ конкретные значения получим график зависимости K(A):