Построение переходных процессов

Построим переходные процессы Ө(t) и ξ(t).

Для построения переходного процесса Ө(t) воспользуемся формулой (8):

где + C, если Ө > b; I участок

V=

0, если –b ≤ Ө ≤ b; II участок

-C, если Ө < -b. III участок

Т.е. получим три уравнения для трех разных участков:

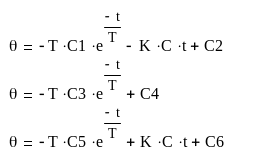
Iучасток

II участок

III участок

Т.к. начальные значения для каждых участков уже были рассчитаны (рассчитывались для построения фазовых портретов), то можно вычислить значения постоянных интегрирования и построить переходный процесс по этим уравнениям.

Графики переходных процессов Ө(t) для различных начальных условий приведены в приложении 1 на рисунке 3 для τ = 0 с. и на рисунке 4 для τ =5 с.

Для построения переходного процесса ξ(t) применим формулу передаточной функции интегрирующего звена:

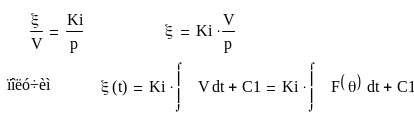
где С1 – постоянная интегрирования.

График переходного процесса ξ(t) приведен в приложении 1 на рисунке 5

Гармоническая линеаризация нелинейного элемента.

Метод гармонической линеаризации является приближенным методом исследования НСАР. Основу этого метода составляют следующие положения.

Пусть имеется нелинейное звено с характеристикой y = F(x). Подадим на вход этого звена гармонический сигнал x = A∙sin ωt. На выходе получим y = F(A∙sin ωt). Этот периодический выходной сигнал можно разложить в ряд Фурье.

Предположим, что наша система обладает тем свойством, что величина амплитудной характеристики на частотах высших гармоник значительно меньше, чем для первой: |Wл(jnω)| << |Wл(jω)|, где n = 2, 3, …

Это свойство называется свойством фильтра линейной части системы. Значит, в силу резонансных и фильтрующих свойств линейной части, на выходе НЭ для расчета периодических режимов можно учитывать только основную, первую гармонику, получим x = A∙sin ωt.

Проведем гармоническую линеаризацию нелинейного элемента для нашего случая:

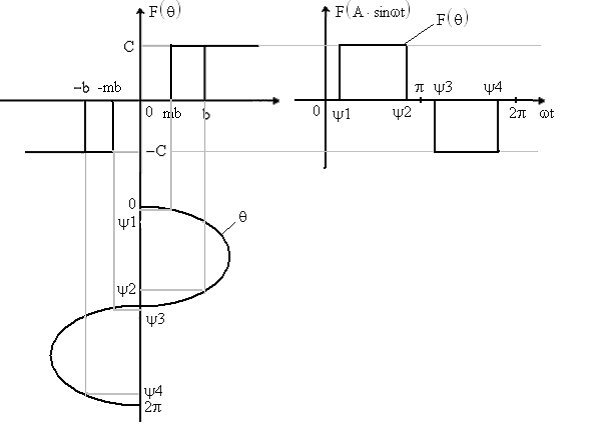
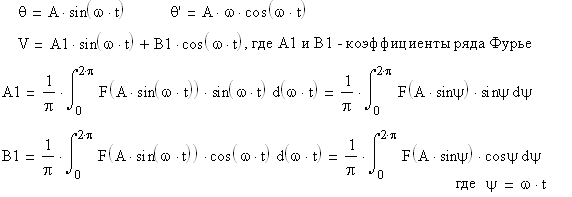
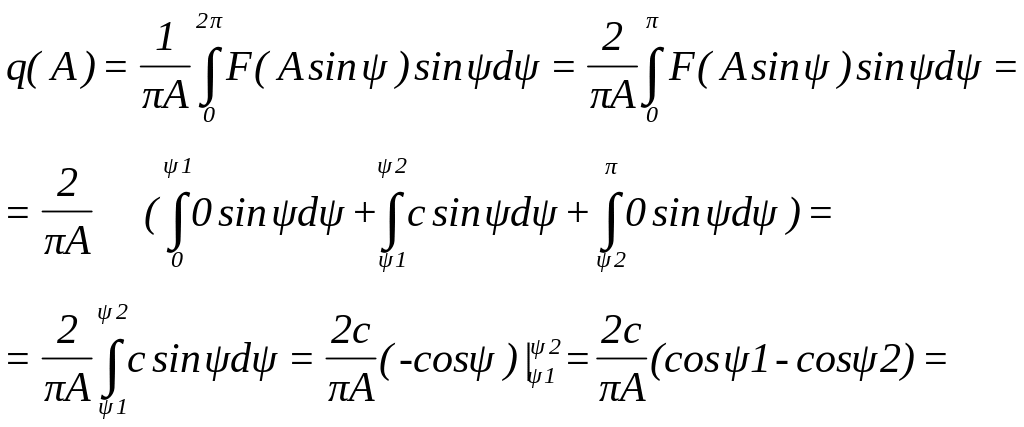
Расчет НСАР частотным методом.

Периодическое решение линеаризованной системы x = A∙sinωt получается при наличии в характеристическом уравнении замкнутой системы пары чисто мнимых корней. А это по критерию Найквиста соответствует прохождению W(jω) через точку -1. Следовательно, периодическое решение определяется неравенством Wл(jω) ∙ Wнэ(A) = -1

1. Расчет для системы без запаздывания, т.е. τ = 0 с.

1. Найдем -Zmin(A) = - π∙b / 2∙C = -0.785

2. Найдем точку пересечения Wл(jω) и отрицательной части вещественной оси:

Все решения уравнения отрицательны, а т.к. значения частоты ω могут быть только положительными, то точки пересечения нет.

Значит в системе нет периодического режима.

2. Расчет для системы с запаздыванием, т.е τ = 5 c.

1. Найдем Zmin(A) = π∙b / 2∙C = 1.309

2. Найдем точку пересечения Wл(jω) и отрицательной части вещественной оси:

Найдем значение Ал(ω) = | Wл (jω) | при ω = ωо:

Получили точку пересечения Wл(jω) и отрицательной части вещественной оси, а т.к. Zmin < Aл(ωo), то существует и точка пересечения Wл(jω) и Zнэ(A).

В системе существует два периодических режима с амплитудами Ап1 и Ап2. Периодический режим с амплитудой Ап = Ап2 будет устойчив, т.к. в этой точке график –Zнэ(A) пересекает график Wл(jω) изнутри наружу.

Найдем Ап:

Решая уравнение получим: Ап1 = 10,013

Ап2 = 196,162

Вывод: В НСАР с запаздыванием (τ = 5 с.) возникают автоколебания с амплитудой Ап = Ап2 = 196,162 и частотой ωп = ωо = 0,217 с^-1.

Графики –Zнэ(A) и Wл(jω) для пунктов 1 и 2 приведены в приложении на рисунке 6 а) и б) соответственно. Распечатка значений координат вблизи точки пересечения графиков –Zнэ(A) и Wл(jω) приведена в приложении 2 пункт 2.