4.2.1. Понятие системы счисления

С истемой счисления (или нумерацией) называют совокупность приёмов построения, обозначения и наименования чисел. Каждая система счисления включает:

1) определённый набор символов (цифр) для записи чисел; эти символы составляют конечный алфавит;

2) определённый способ чтения (наименования) чисел.

Каждой цифре в записи числа однозначно сопоставляется количество, выражаемое этой цифрой. Это количество будем называть количественным эквивалентом цифры¹.

По способу определения количественного эквивалента цифры в записи числа все системы счисления можно разбить на два класса: непозиционные и позиционные.

С истема счисления называется непозиционной, если каждой цифре и в любом месте в записи числа однозначным образом сопоставлен некоторый количественный эквивалент. Таким образом, в непозиционных системах счисления местоположение цифры в записи числа (позиция) не влияет на её количественный эквивалент.

Примером непозиционной системы счисления является римская система². Количественные эквиваленты цифр римской системы счисления равны: (I) = l; (V) = 5; (X) = 10; (L) = 50; (С) = 100; (D) = 500; (М) = 1000.

Количественный эквивалент числа в римской системе счисления определяется по следующему правилу: если в записи числа слева от символа находится символ, имеющий не меньший количественный эквивалент, то этот количественный эквивалент включается в сумму со знаком «плюс», в противном случае  со знаком «минус». Например, количественные эквиваленты чисел CCXXXIX и DCCXL равны: …….(CCXXXIX) = 10  1 + 10 + 10 + 10 + 100 + 100 = 239,

(DCCXL) = 50 –10 + 100 + 100 + 500 = 740.

Исторически вначале появились непозиционные системы счисления. Общим недостатком этих систем счисления является трудность записи в них больших чисел: либо эти записи слишком громоздки, либо алфавит цифр весьма велик. Именно поэтому непозиционные системы счисления в вычислительной технике практически не нашли применения.

С истема счисления называется позиционной, если количественный эквивалент цифры определяется не только видом самой цифры, но и её местоположением в записи числа  позицией.

Примером такой системы является широко используемая нами десятичная система. При смене позиции (места) цифры в числе меняется её количественный эквивалент. Например, у числа 333,3 первая цифра справа означает «три десятых долей единицы», вторая «три единицы», третья – «три десятка», а четвёртая – «три сотни». Сама же запись 333,3 означает сокращённую запись выражения 300 + 30 + + 3 + 0,3 = 310² + 310¹ + 310⁰ + 310 ^–1 = 333,3.

Любая позиционная система счисления характеризуется своим основанием.

О снование позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание системы можно принять любое натуральное число – два, три, четыре и т.д.

Наиболее широкое использование имеют следующие системы счисления:

• десятичная (используются цифры 0, 1, 2, ..., 9);

• двоичная (используются цифры 0, 1);

• восьмеричная (используются цифры 0, 1, 2, ..., 7);

• шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, 2, ..., 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).

Любое число А в позиционной системе счисления можно записать в общем виде³:

А_(p) = ,

где a_i – цифра в i-том разряде записи числа в системе счисления с основанием р.

Для определения номера разряда (значения i) используется простое правило (см. рис. 4.7): первый слева от запятой разряд (точка отсчёта) является нулевым; номера остальных разрядов равны их порядковому номеру относительно нулевого разряда: влево (целая часть числа) – со знаком «+» (при записи опускается); вправо (дробная часть числа) – со знаком «–». Например,

324,54₍₁₀₎ = 310² + 210¹ + 410⁰ + 510^–1 + 410^–2,

1101,01₍₂₎ = 12³ + 12² + 02¹ +12⁰ + 02^–1 + 12^–2,

352,51₍₈₎ = 38² + 58¹ + 28⁰ + 58^-1 + 18^–2,

A4C,3F₍₁₆₎ = 1016² + 416¹ + 1216⁰ + 316^–1 + 1516^–2.

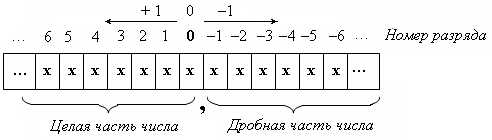
Рис. 4.7. Принцип нумерации разрядов записи числа