Лекція 5

Короткий зміст|вміст,утримання|: Приведення сили до заданого центру. Приведення системи сил до заданого центру. Умови рівноваги просторової системи паралельних сил. Умови рівноваги плоскої системи сил. Теорема про три моменти. Статично визначені і статично невизначені завдання|задачі|. Рівновага системи тіл.

Приведення системи сил до заданого центру. Приведення сили до заданого центру

Р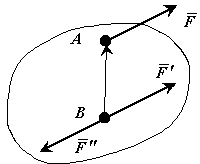 івнодіюча|рівнодійна| системи сил, що сходяться, безпосередньо знаходиться|перебуває| за допомогою складання сил за правилом паралелограма. Очевидно, що аналогічну задачу можна буде вирішити і для довільної системи сил, якщо знайти для них метод, що дозволяє перенести всі сили в одну точку|точку|.

Рисунок 5-1

Теорема про паралельне перенесення|перенос| сили. Силу, прикладену до абсолютно твердого тіла, можна, не змінюючи|зраджувати| дії, що надається|робить,виявляє,чинить| нею, переносити з|із| даної точки|точки| в будь-яку іншу точку тіла, додаючи при цьому пару з|із| моментом, який дорівнює моменту сили, що переноситься відносно|відносно| точки|точки|, куди сила переноситься.

Хай|нехай| сила прикладена в точці A. Дія цієї сили не змінюється, якщо в точці B прикласти дві врівноважені сили. Отримана|одержувати| система трьох сил є силою , яка дорівнює , але|та| прикладену в точці|точці| В і пару з|із| моментом . Процес заміни сили силою|силоміць| і парою сил називається приведенням сили до заданого центру В .

Приведення системи сил до заданого центру

Основна теорема статики (Пуансо)

Будь-яку довільну систему сил, що діє на тверде тіло, можна в загальному|спільному| випадку привести до сили і пари сил. Цей процес заміни системи сил однією силою і однією парою сил називається приведенням системи сил до заданого центру.

Головним вектором системи сил називається вектор, який дорівнює векторній сумі цих сил.

Головним моментом системи сил відносно|відносно| точки|точки| О тіла, називається вектор, який дорівнює векторній сумі моментів всіх сил системи відносно|відносно| цієї точки|точки|.

Формули для обчислення|підрахунку| головного вектора і головного моменту

Формули для обчислення|підрахунку| модуля і направляючих|спрямовувати,скеровувати| косинусів головного вектора і головного моменту

Умови рівноваги системи сил

Векторна форма

Для рівноваги довільної системи сил, прикладених до твердого тіла, необхідно і достатньо|досить|, щоб|аби| головний вектор системи сил дорівнював нулю і головний момент системи сил відносно|відносно| будь-якого центру приведення також дорівнював нулю.

Алгебраїчна форма

Для рівноваги довільної системи сил, прикладених до твердого тіла, необхідно і достатньо|досить|, щоб|аби| три суми проекцій всіх сил на осі декартових координат дорівнювали нулю і три суми моментів всіх сил відносно трьох осей координат також дорівнювали нулю.

Умови рівноваги просторової системи паралельних сил

На тіло діє система паралельних сил. Розташуємо вісь Oz| паралельно силам.

Рівняння

Для рівноваги просторової системи паралельних сил, що діють на тверде тіло, необхідно і достатньо|досить|, щоб|аби| сума проекцій цих сил дорівнювала нулю і суми моментів цих сил відносно двох координатних осей, перпендикулярним силам, також дорівнювали нулю.

- проекція сили на вісь Oz|.