Аксіоми статики

А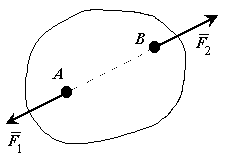 ксіома про рівновагу двох сил. Якщо на вільне абсолютно тверде тіло діють дві сили, то тіло може знаходитися|перебувати| в рівновазі тоді і тільки|лише| тоді, коли ці сили рівні по величині і направлені|спрямовані| вздовж|вздовж,уподовж| однієї прямої в протилежні| сторони.

Рисунок 2-1

А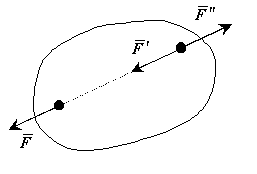 ксіома про додавання|добавляти| (відкиданні) урівноваженої системи сил. Якщо на тверде тіло діє система сил, то до неї можна додати|добавляти| (відкинути) врівноважену систему сил. Отримана|одержувати| після|потім| додавання|добавляти| (відкидання) нова система сил еквівалентна первинною.

Рисунок 2-2

Аксіома паралелограма сил. Дві сили, прикладені до тіла в одній точці|точці| мають рівнодіючу|рівнодійну|, прикладену в тій же крапці|точці| і рівну по величині і напряму|направленню| діагоналі паралелограма, побудованого|спорудити| на цих силах, як на сторонах.

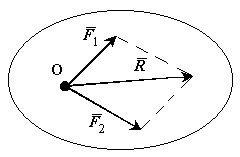
Ця аксіома допускає і зворотне твердження|затвердження|:

Силу можна розкласти безліччю способами на дві сили, прикладені в будь-якій точці лінії дії даної сили.

Рисунок 2-3

А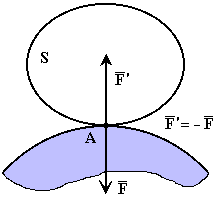 ксіома про рівність дії і протидії. При всякій|усякій| дії одного матеріального тіла на інше має місце така ж по величині, але|та| протилежна за напрямом|направленню| протидія.

Якщо до даного тіла прикладена сила дії від іншого тіла, то від даного тіла до іншого тіла буде прикладена сила , яка дорівнює і прямо протилежна силі . Сили прикладені в одній геометричній точці, але|та| до різних тіл.

Рисунок 2-4

Вільним твердим тілом називається тіло, що має можливість|спроможність| отримувати|одержувати| будь-який рух з|із| даного положення|становища|, для чого необхідно прикласти відповідну силу.

При вирішенні більшості завдань|задач| механіки доводиться мати справу|річ| з|із| тілами позбавленими можливості|спроможності| переміщатися у напрямі дії прикладених до них активних сил.

Тіла, що обмежують рух даного тіла, називаються зв'язками.

Сила, з|із| якою зв'язок діє на тіло, перешкоджаючи його переміщенню в тому або іншому напрямі|направленні| називається силою|силоміць| реакції (протидії) цього зв'язку або просто реакцією зв'язку.

А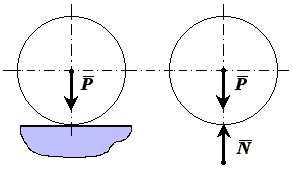 ксіома про зв'язки. Ефект від дії зв'язків такий же, як від дії певних, додаткових сил, які можуть бути прикладені до вільного тіла замість зв'язків.

Аксіому про зв'язки називають також принципом визволення| від зв'язків. Згідно|згідно з| цій аксіомі, не змінюючи|зраджувати| рівноваги тіла, кожен зв'язок можна відкинути, замінивши її реакцією зв'язку.

Сили, які можуть повідомляти вільному тілу Рисунок 2-5 рух, називаються активними силами.

Приклавши до тіла, окрім|крім| активних сил, реакції зв'язків, можна розглядати|розглядувати| тіло як вільне. Активні сили і сили реакції називаються зовнішніми силами.

Наприклад, на гладкій нерухомій горизонтальній площині|плоскості| покоїться куля(рисунок 2-5), площина|плоскість|, що обмежує рух кулі, є|з'являється,являється| для нього зв'язком. Якщо звільнити|визволяти| кулю від зв'язку, то для утримання його у спокої до нього в точці дотику з|із| площиною|плоскістю| потрібно прикласти силу , рівну по модулю ваги кулі і протилежну йому за напрямом|направленню|. Сила і є реакція площини|плоскості| (реакція зв'язку). Куля, звільнена|визволяти| від зв'язку, буде вільним тілом, на яке діє сила , що задається (активна), і реакція площини|плоскості| .