
- •Лекція 1 Вступ|вступ|
- •Статика - це розділ теоретичної механіки, в якому висловлюється|викладає| загальне|спільне| вчення про сили і вивчаються умови рівноваги матеріальних тіл, що знаходяться|перебувають| під дією сил.
- •1. Поняття вектора
- •2. Праві і ліві системи координат
- •3. Довжина проекції і направляючі|спрямовувати,скеровувати| косинуси вектора
- •5. Векторний добуток|добуток| двох векторів
- •Лекція 2
- •Основні поняття і визначення статики
- •Аксіоми статики
- •Теореми статики
- •Лекція 3
- •З'єднання|сполучення,сполука| тіл між собою
- •Тіла, що контактують з|із| поверхнею
- •Зв'язок за допомогою ниток (нитка, ланцюг|цеп|, трос)
- •З'єднання|сполучення,сполука| тіл за допомогою шарнірів
- •Жорстке затиснення
- •Система сил, що сходиться
- •Умови рівноваги системи сил, що сходяться у векторній формі
- •Умови рівноваги системи сил, що сходяться в алгебраїчній формі
- •Момент сили відносно|відносно| осі
- •Зв'язок моменту сили відносно|відносно| осі з|із| моментом сили відносно|відносно| точки|точки|
- •Формули для моментів сили відносно|відносно| осей координат
- •Лекція 4
- •Лекція 5
- •Приведення системи сил до заданого центру. Приведення сили до заданого центру
- •Приведення системи сил до заданого центру
- •Умови рівноваги системи сил
- •Умови рівноваги просторової системи паралельних сил
- •Теорема про момент рівнодіючої (теорема Варіньона)
- •Умови рівноваги плоскої системи сил
- •Теорема про три моменти
- •Лекція 7
- •Тертя Тертя ковзання
- •Кінематика Лекція 1
- •Кінематика точки|точки|
- •Швидкість точки|точки|
- •Швидкість точки|точки| при векторному способі завдання|задавання| руху
- •Лекція 2
- •Природний трикутник
- •Диференціювання одиничного|поодинокого| вектора
- •Рівномірний рух
- •Рух який рівномірно змінюється
- •Лекція 3
- •Лекція 4
- •Кінематика твердого тіла
- •Міри свободи твердого тіла
- •Рівномірне обертання
- •Обертання яке рівномірно змінюється
- •Лекція 5
- •Лекція 6
- •Теорема про прискорення точок плоскої фігури
- •Миттєвий центр прискорень
- •Приклади знаходження мцп.
- •Динаміка Лекція 1
- •Вступ|вступ|
- •Аксіоми класичної механіки
- •Системи одиниць
- •Лекція 2
- •Лекція 3
- •Загальні|спільні| теореми динаміки точки|точки|
- •Кількість руху точки|точки|
- •Елементарний і повний|цілковитий| імпульс сили
- •Теорема про зміну кількості руху точки|точки|
- •Момент кількості руху точки|точки|
- •Теорема про зміну моменту кількості руху точки|точки|
- •Робота сили. Потужність
- •Кінетична енергія точки|точки|
- •Теорема про зміну кінетичній енергії точки|точки|
- •Принцип Даламбера для матеріальної точки|точки|
- •Лекція 4
- •Лекція 5
- •Лекція 6
- •Кількість руху системи
- •Теорема про зміну кількості руху системи
- •Закони збереження|зберігання| кількості руху
- •Теорема про рух центру мас
- •Момент кількості руху системи
- •Момент кількості руху твердого тіла відносно|відносно| осі обертання при обертальному русі твердого тіла
- •Закони збереження|зберігання| моменту кількості руху
- •Кінетична енергія системи
- •Кінетична енергія твердого тіла
- •Теорема про зміну кінетичній енергії системи
Момент кількості руху твердого тіла відносно|відносно| осі обертання при обертальному русі твердого тіла
О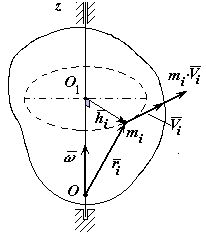 бчислимо|обчислятимемо,вичислятимемо|
момент кількості руху твердого тіла
відносно|відносно|
осі обертання.
бчислимо|обчислятимемо,вичислятимемо|
момент кількості руху твердого тіла
відносно|відносно|
осі обертання.
![]()
![]()
![]()
Момент кількості руху твердого тіла
![]()
відносно|відносно| осі обертання при обертальному русі дорівнює добутку|добутку| кутової швидкості тіла на його момент інерції відносно|відносно| осі обертання
Рисунок 6-1
Теорема про момент кількості руху системи який змінюється
Теорема. Похідна за часом від моменту кількості руху системи, взятого відносно|відносно| будь-якого|будь-якого| центру, дорівнює векторній сумі моментів зовнішніх сил, що діють на систему відносно|відносно| того ж центру.
![]() (6-3)
(6-3)
Доказ: Теорема про зміну моменту кількості руху для точки|точки| має вигляд|вид|:
![]() ,
,
Складемо всі рівнянь і отримаємо|одержуватимемо|:
![]() або
,
або
,
що і потрібно було довести.
Теорема. Похідна за часом від моменту кількості руху системи, взятого відносно|відносно| будь-якої осі, дорівнює векторній сумі моментів зовнішніх сил, що діють на систему відносно|відносно| тієї ж осі.
Для доказу досить спроектувати векторне рівняння (6-3) на цю вісь. Для осі це виглядатиме так:
![]() (6-4)
(6-4)
Теорема про зміну моменту кількості руху системи відносно|відносно| центру мас (без доказу).
Для осей рухомих поступально разом з центром мас системи теорема про зміну моменту кількості руху системи відносно|відносно| центру мас зберігає той же вигляд|вид|, що і відносно|відносно| нерухомого центру.
Закони збереження|зберігання| моменту кількості руху
1.
Якщо головний момент зовнішніх сил
системи відносно|відносно|
точки|точки|
дорівнює нулю (![]() ),
то момент кількості руху системи
відносно|відносно|
точки|точки|
постійний по величині і напряму|направленню|
),
то момент кількості руху системи
відносно|відносно|
точки|точки|
постійний по величині і напряму|направленню|
![]()
2.
Якщо сума моментів всіх зовнішніх сил
системи відносно|відносно|
будь-якої осі дорівнює нулю (![]() ),
то момент кількості руху системи
відносно|відносно|
цієї осі є|з'являється,являється|
постійною величиною
),
то момент кількості руху системи
відносно|відносно|
цієї осі є|з'являється,являється|
постійною величиною
![]()
Кінетична енергія системи
Кінетичною енергією системи називають суму кінетичних енергій всіх точок системи.
![]()
Теорема Кеніга. Кінетична енергія системи в абсолютному русі складається з|із| кінетичної енергії центру мас, якщо в ньому зосередити всю масу системи, і кінетичної енергії системи при її русі відносно|відносно| центру мас.
![]()
Д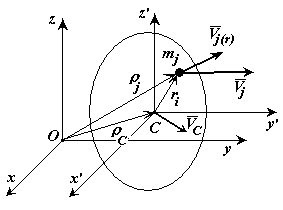 оказ:
Розглянемо|розглядуватимемо|
рух механічної системи відносно двох
систем координат. Одна система нерухома,
інша, з|із|
початком в центрі мас системи, переміщається
відносно|відносно|
першої поступально.
оказ:
Розглянемо|розглядуватимемо|
рух механічної системи відносно двох
систем координат. Одна система нерухома,
інша, з|із|
початком в центрі мас системи, переміщається
відносно|відносно|
першої поступально.
![]() -
радіус-вектор і абсолютна швидкість
точки|точки|
відповідно;
-
радіус-вектор і абсолютна швидкість
точки|точки|
відповідно;
![]() -
радіус-вектор і абсолютна швидкість
центру мас системи відповідно;
-
радіус-вектор і абсолютна швидкість
центру мас системи відповідно;
![]() -
радіус-вектор точки|точки|
відносно|відносно|
центру мас і відносна швидкість цієї
точки|точки|
відповідно.
-
радіус-вектор точки|точки|
відносно|відносно|
центру мас і відносна швидкість цієї
точки|точки|
відповідно.
![]()
![]() (оскі-
Рисунок 6-2 льки|тому
що|
переносний рух поступальний)
(оскі-
Рисунок 6-2 льки|тому
що|
переносний рух поступальний)

Оскільки|тому
що|,
то
![]() або
або
Кінетична енергія твердого тіла
Поступальна хода тіла
Кінетична енергія твердого тіла при поступальній ході обчислюється|обчисляє,вичисляє| так само, як і для однієї точки|точки|, у|біля,в| якої маса дорівнює масі цього тіла.
![]() -
швидкість будь-якої точки твердого
тіла.
-
швидкість будь-якої точки твердого
тіла.
Обертання тіла навколо|навкруг,довкола| нерухомої осі
Кінетична енергія твердого тіла при обертальному русі навколо|навкруг,довкола| нерухомої осі дорівнює половині добутку|добутку| моменту інерції тіла відносно|відносно| осі обертання на квадрат кутової швидкості тіла.
![]() -
кутова швидкість обертання твердого
тіла.
-
кутова швидкість обертання твердого
тіла.
Плоский рух тіла
Кінетична енергія твердого тіла при плоскому русі складається з|із| кінетичної енергії тіла разом з центром мас і кінетичної енергії тіла від обертання навколо|навкруг,довкола| осі, що проходить через центр мас і перпендикулярної площини|плоскості| руху.
![]() -
швидкість центру мас твердого тіла,
-
швидкість центру мас твердого тіла,
![]() - кутова швидкість обертання твердого
тіла.
- кутова швидкість обертання твердого
тіла.
