Швидкість точки|точки|
О
днією
з основних характеристик руху точки|точки|
є|з'являється,являється|
її швидкість відносно|відносно|
вибраної системи відліку.
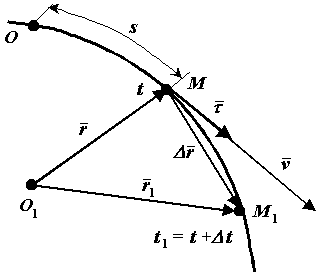
Швидкість точки|точки| при векторному способі завдання|задавання| руху
Положення|становище|
рухомої точки М
відносно|відносно|
системи відліку у момент часу
визначається радіус-вектором
.
В інший момент часу
точка|точка|
займе|позичатиме,посідатиме|
положення|становище|
М1
з|із|
радіус-вектором
.
За час
радіус-вектор рухомої точки|точки|
зміниться на
( рисунок 1-4).
Рисунок 1-4
Середньою
швидкістю
називається відношення|ставлення|
зміни радіус-вектора
до зміни часу
.
(1-4)
Швидкість точки|точки| дорівнює першій похідній за часом від її радіус-вектора.
(1-5)
Швидкість точки|точки| при координатному способі завдання|задавання| руху
Розкладемо радіус-вектор і швидкість на складові, паралельні осям координат. Отримаємо|одержуватимемо|:
(1-6)
Після|потім| диференціювання
(1-7)
Звідси слідує
(1-8)|прямує|
Проекція швидкості точки|точки| на яку-небудь координатну вісь дорівнює першій похідній за часом від відповідної координати цієї точки.
Модуль швидкості і направляючі|спрямовувати,скеровувати| косинуси дорівнюють:
Якщо точка|точка| рухається|суне| в площині|плоскості|, то, вибравши осі координат Oх| і Oу| в цій площині|плоскості|, отримаємо|одержуватимемо|:
Для прямолінійного руху точки|точки| координатну вісь, наприклад вісь Oх|, направляємо|спрямовуємо,скеровуємо| по траєкторії. Тоді
Швидкість точки|точки| при природному способі завдання|задавання| руху
Хай|нехай| швидкість точки|точки| задана природним способом, тобто задані траєкторія точки|точки| і закон її руху по траєкторії .
Обчислимо|обчислятимемо,вичислятимемо| швидкість точки.|точки|
Використовуємо
радіус-вектор
рухомої точки|точки|,
початок|розпочинало,зачинало|
якого знаходиться|перебуває|
в нерухомій точці|точці|
- одиничний|поодинокий|
вектор, направлений|спрямований|
по дотичній до траєкторії у бік зростаючих
відстаней
Рисунок
1-5
. (1-9)
При
напрями|направлення|
векторів
і
співпадають|збігаються|.
Якщо точка|точка|
рухається|суне|
у бік відстані, що зменшується , то
і напрями|направлення|
векторів
і
протилежні.
При
вектор швидкості направлений|спрямований|
по
, тобто у бік зростаючих відстаней; при
він має напрям|направлення|,
протилежний
, тобто у бік відстані, що зменшується
.
- алгебраїчна
швидкість точки|точки|,
проекція швидкості
на позитивний напрям|направлення|
дотичній до траєкторії.
Природне завдання|задавання| руху точки|точки| повністю|цілком| визначає швидкість за величиною і напрямом|направленню|.