15. Определение площади контактной поверхности графоаналитическим методом по а.А. Диннику

В его основе использован графический метод в соответствии, с которым строится только две проекции: продольная и поперечная.

Отрезок М соответствует по своему физическому смыслу длине очага деформации в заданном сечении. Тогда отрезок АВ равен обжатию в этом сечении, а отрезок от оси О до точке В- катающему радиусу, тогда

16)Определение площади контактной поверхности аналитическим методом.

Аналитический метод основан на использовании формул аналитической геометрии, рассматривающей схему взаимодействия раската и калибра. Для ряда простых калибров

т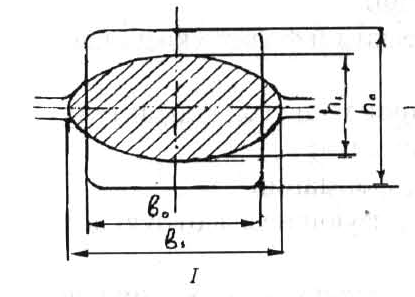 акие формулы разработаны В.Г. Дроздом

При прокатке в калибрах других сложных форм Fк определяется с использованием след. аналитической формулы:

Rcp и hcp – определяются по методу приведенной полосы, который заключается в том,что калибр и полоса любой формы приводятся к прямоугольному профилю той же

квадратный раскат в ширины

овальном калибре

где: и - начальная и конечная высота полосы полученные после перерасчета

- идеальный радиус, равный половине расстояния между осями валков. Погрешность метода составляет 7-18 %

17.Условие свободного начального захвата.

Если заталкивающая сила Q не вызывает смятия кромок, то такой захват называется свободным или естественным.

Рассмотрим силы, которые действуют на валки и полосу в момент захвата. Силы трения Т стремятся увлечь раскат в зев валков, а нормальные силы N – вытолкнуть. Разложим силы N и T на составляющие.Для осуществления захвата необходимо чтобы выполнялось неравенство

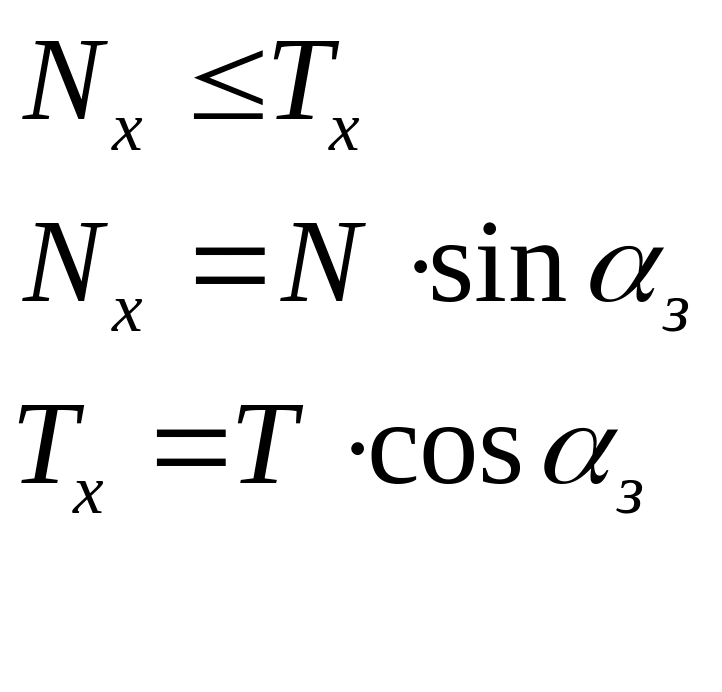
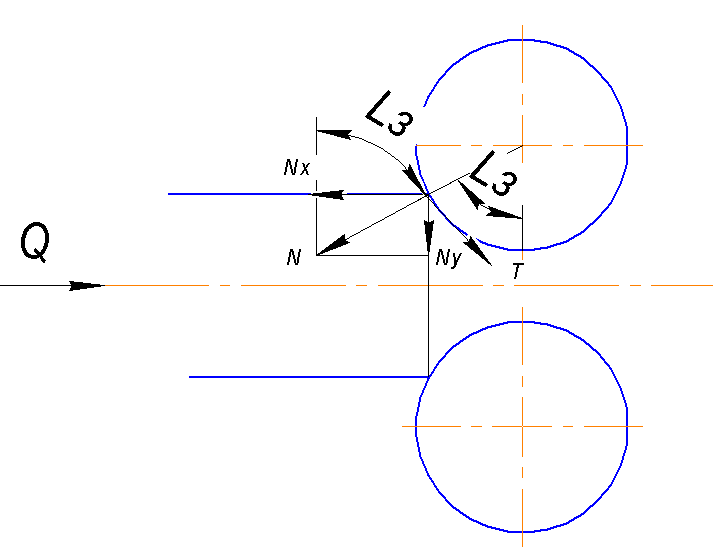
Пользуясь законом трения Амантона-Кулона и произведя преобразования получим

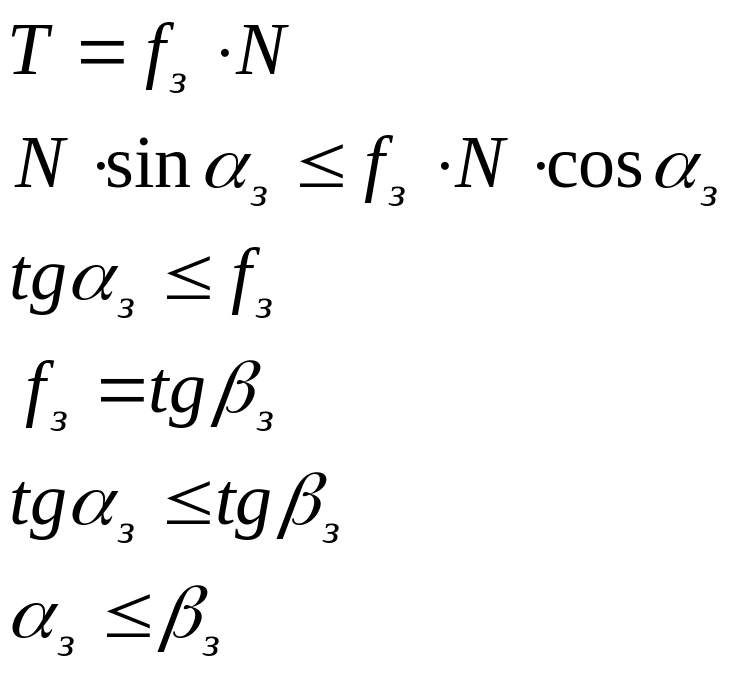
β_з-угол трения при захвате

18.Принудительный захват.

В тех случаях, когда заталкивающая сила Q велика и способна осуществить значительное смятие кромок (вдавливание металла в валки) то такой захват называется принудительным или искусственным. При очень больших значениях Q возможна реализация процесса α_з≥β_з – исключение.

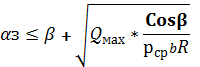- условие принудительного захвата

При β=0, α≤ какого то значения, то есть реализация процесса возможна, но в этом случае реализованный процесс будет процессом продавливания, а не прокаткой.

Увеличение заталкивающей силы Q вызывает ответный рост отталкивающей силы N, таким образом сила Q сама по себе не может создать перевеса втягивающих сил над отталкивающими.

Сила Q приводит к сжатию кромок в результате чего сила N смещается внутрь очага деформации и происходит благоприятный разворот сил в очаге деформации для условия захвата. Когда угол произойдет истинный захват. Под действием силы Q наблюдается раздвижение валком.

Заталкивающая сила максимальна, когда угол равен углу трения .

19. Динамический захват.

Захват по своей природе является динамическим процессом в котором всегда участвуют инерционные силы.

(масса на ускорение).

m-масса тела

dV- изменение скорости тела за время d

Введем инерционные составляющие и запишем в уравнение равновесия.

Рассмотрим 4 характерных случая взаимодействия полосы с валками:

1) классический случай процесса прокатки

V_o- скорость подвода полосы к валкам;

V_B- окружная скорость валков

Втягивает сила 2(T_x-N_x)>0 в очаг деформации при этом V_o <V_B полоса начнет двигаться с ускорением до тех пор пока V_o =V_B (+/+)

В том случае, когда втягивающая сила 2(T_x-N_x) мала, а разница V_o -V_B – велика, полоса начинает двигаться не устойчиво, т.е. с подергиванием и рывками. Для улучшения процесса надо уменьшить разницу V_o -V_B

2)

В начальный момент произойдет удар

+/- - силы трения силы инерции

Полоса движется с замедлением до тех пор пока скорость передней кромки не станет равна V_B.

После этого силы трения меняют знак на противоположный и становятся втягивающими и идет нормальный процесс прокатки.

3)

В начальный момент касания сила T_x положительна (она хочет втянуть металл в валки), но 2(T_x-N_x)<0. В этот момент включается инерция и вдавливает металл в очаг деформации. Если величины инерционной силы хватит, что бы , то захват произойдет. Если нет, то скорость упадет до 0.

4)

Удар, сила T_x<0, инерционные силы больше 0. полоса тормозится пока V_o =V_B, а T_x становится >0, если выполняется условие , то процесс прокатки начнется, если нет, то полоса начнет тормозится пока не остановится или пока не выполнится условие.

20. Условие захвата при установившемся процессе прокатки.

Д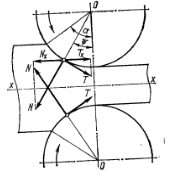 ля вывода условия захвата при установившемся процессе рассмотрим предельный момент прокатки, когда все силы трения полностью используются, как втягивающие. В этом случае только одна зона скольжения и все силы трения приводятся к одной силе T (на одном валке) перпендикулярно к силе N.

В этом случае процесс прокатки идет до тех пор пока

, где - коэф. трения при установившемся процессе прокатки.

Подставим в это выражение и получаем:

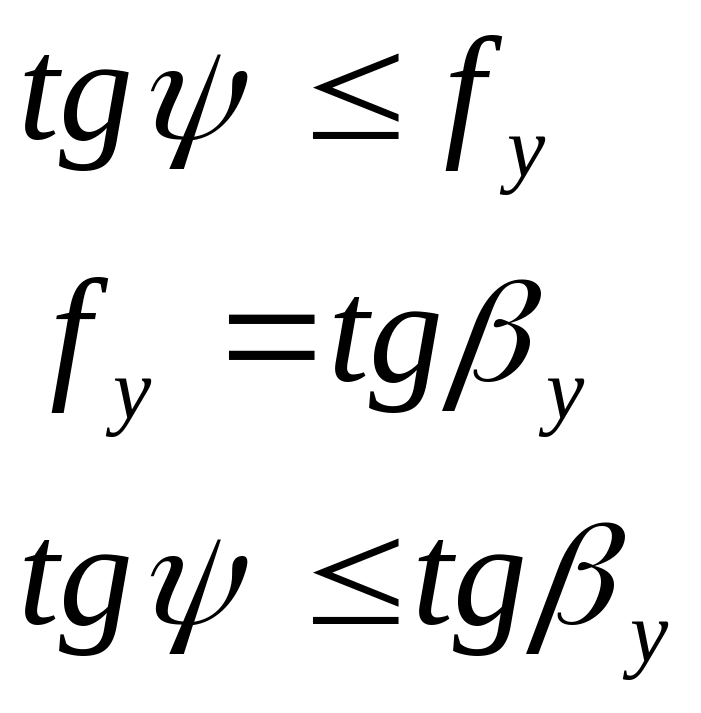
- угол трения при установившемся процессе прокатки.

- условие захвата при установившемся процессе.

- точка приложения равнодействующей силы.

Использование данной формулы неудобно, т.к. неизвестно.

Считают, что силы N и T приложены по середине дуги контакта, т.е. - условие захвата при установившемся процессе.

Из данного неравенства следует, что процесс прокатки реализуется во всех случаях пока угол контакта меньше удвоенного угла трения ( ).

Условие проверяется при прокатке клинообразных образцов