
- •1.Предмет, метод, задачи статистики
- •Комплексный анализ рядов распределения
- •12. Графическое изображение рядов распределения.
- •13. Характеристика центра распределения.
- •Xmo0-нижняя граница модального интервала
- •14. Характеристика структуры распределения.
- •2. Характеризует выпад вершины эмпирического распределения вверх или вниз по отношению к вершине нормального распределения.
- •16. Выравнивание эмпирических распределений, выбор типа закономерности распределения.
- •21. Определение доверительных интервалов.
- •Практические задачи, решаемые с помощью корреляционно-регрессионный анализа (кра):
- •Оценка статистической значимости уравнения регрессии его параметров.
- •34. Задачи изучения динамических рядов.
- •37. Сглаживание рядов динамики.
- •- Стандартная ошибка (ср.Кв. Отклонение)
- •40. Автокорреляция уровней рядов динамики.
- •43. Корреляция рядов динамики
- •44. Экстраполяционное прогнозирование.
- •- Стандартная ошибка (ср.Кв. Отклонение)
- •47. Агрегатные индексы
- •48. Индексы Ласпераса, Паше, Фишера. Индекс-дефлятор.
- •49. Правило выбора весов.
- •50. Индексы средние из индивидуальных
37. Сглаживание рядов динамики.
Механическое
выравнивание проводится
в основном путем укрупнения временных
интервалов или с использованием
скользящей средней: по исходному ряду
включая, например, 3 первых уровня
рассчитывается средняя величина, и
полученная величина относится к середине
интервала. Далее рассчитывается среднее
значение по трем уровням, но начиная со
второго. Полученное средне значение
относится к середине интервала, но к
3-му уровню. Если для определения
скользящей средней используется четно
число уровней (например 4), то получаемая
средняя величина попадает в интервал
м/у 2-ым и 3-им уровнем. Следующее среднее
значение попадает в интервал м/у 3-им и
4-ым уровнями. В этих условиях необходимо
применить так называемое центрирование
– когда выровненный уровень будет
рассчитываться как средняя арифметическая
м/у 2-мя скользящими средними:
![]() . Чем > период скольжения, тем более
отчетливо выявляется основная тенденция.
Однако, с увеличением периода скольжения
более существенно сокращается
анализируемый ДРяд, что отрицательно
сказывается на построении моделей.
Аналитическое
выравнивание
в отличие от механического, позволяет
не только более отчетливо увидеть
основную тенденцию развития изучаемого
явления, но и получить аналитическую
форму изучаемого временного ряда, точнее
его основной тенденции.
. Чем > период скольжения, тем более
отчетливо выявляется основная тенденция.
Однако, с увеличением периода скольжения
более существенно сокращается
анализируемый ДРяд, что отрицательно
сказывается на построении моделей.
Аналитическое
выравнивание
в отличие от механического, позволяет
не только более отчетливо увидеть
основную тенденцию развития изучаемого
явления, но и получить аналитическую
форму изучаемого временного ряда, точнее
его основной тенденции.
Эта
аналитическая форма получила название
трендовой модели. Трендовая модель
представляет собой уравнение регрессии,
в котором в качестве признака результата
выступает уровень изучаемого ряда, а в
качестве фактора – время. Уравнение
тренда:
![]() ,
где , где y
–уровень ряда, t-время.
Т.е. уровень ряда есть функция времени.
Однако следует понимать, что изменение
уровней временного ряда (конкретных
экономических показателей) происходит
не потому что год сменяется годом, а
потому что меняется проявление конкретных
внутренних и внешних факторов. Время в
трендовой модели выступает совокупным
фактором, за изменением которого следует
видеть изменение конкретных экономических
и других факторов. Построение трендовой
модели предполагает выбор формы модели
и расчет параметров уравнения. Ошибка
в выборе формы тренда более существенно
сказывается на прогнозе, чем ошибка в
расчете параметров. Прежде чем приступить
к определению формы трендовой модели,
т.е. модели, описывающей основную
тенденцию изучаемого явления, следует
убедиться в наличии самого тренда, т.е.
тенденции развития. Ряд, в котором
отсутствует тенденция называется
стационарным. Уровни таких рядов
колеблются вокруг средних значений,
отклонения от которых есть случайные
колебания. Стационарные ряды чаще всего
можно видеть в рядах, построенных по
относительным и средним показателям.
Для того, чтобы определить наличие
тенденции в изучаемом ДРяду, ряд разбивают
на 2 ~ равных периода и рассчитывают
значение среднего уровня по каждому из
них. Затем с использованием t-статистики
проверяется о несущественности различий
м/у полученными средними:
,
где , где y
–уровень ряда, t-время.
Т.е. уровень ряда есть функция времени.
Однако следует понимать, что изменение
уровней временного ряда (конкретных
экономических показателей) происходит
не потому что год сменяется годом, а
потому что меняется проявление конкретных
внутренних и внешних факторов. Время в
трендовой модели выступает совокупным
фактором, за изменением которого следует
видеть изменение конкретных экономических
и других факторов. Построение трендовой
модели предполагает выбор формы модели
и расчет параметров уравнения. Ошибка
в выборе формы тренда более существенно
сказывается на прогнозе, чем ошибка в
расчете параметров. Прежде чем приступить
к определению формы трендовой модели,
т.е. модели, описывающей основную
тенденцию изучаемого явления, следует
убедиться в наличии самого тренда, т.е.
тенденции развития. Ряд, в котором
отсутствует тенденция называется
стационарным. Уровни таких рядов
колеблются вокруг средних значений,
отклонения от которых есть случайные
колебания. Стационарные ряды чаще всего
можно видеть в рядах, построенных по
относительным и средним показателям.
Для того, чтобы определить наличие
тенденции в изучаемом ДРяду, ряд разбивают
на 2 ~ равных периода и рассчитывают
значение среднего уровня по каждому из
них. Затем с использованием t-статистики
проверяется о несущественности различий
м/у полученными средними:
![]() .
T-статистика
рассчитывается:
.
T-статистика
рассчитывается:
 ,где
сигма – среднее квадратическое отклонение
разности средних (стандартная ошибка).
Стандартная ошибка рассчитывается
исходя из дисперсий по каждому временному
отрезку и рассчитывается как средняя
арифметическая взвешенная:
,где
сигма – среднее квадратическое отклонение
разности средних (стандартная ошибка).
Стандартная ошибка рассчитывается
исходя из дисперсий по каждому временному
отрезку и рассчитывается как средняя
арифметическая взвешенная:
 .
Поскольку временные ряды не очень
длинные, то стандартная ошибка считается
по правилу малой выборки, т.е. учитывается
не только n,
а (n-1).
Полученное значение t
статистики сравнивается с табличным
значением, и если tф≥tтабл,
то нулевая гипотеза отвергается и
принимается альтернативная о существенности
различий в средних величинах, полученных
по двум временным отрезкам. Что будет
свидетельствовать о наличии тенденции
в изучаемом временном ряду.
.
Поскольку временные ряды не очень
длинные, то стандартная ошибка считается
по правилу малой выборки, т.е. учитывается
не только n,
а (n-1).
Полученное значение t
статистики сравнивается с табличным
значением, и если tф≥tтабл,
то нулевая гипотеза отвергается и
принимается альтернативная о существенности
различий в средних величинах, полученных
по двум временным отрезкам. Что будет
свидетельствовать о наличии тенденции
в изучаемом временном ряду.
38. Понятие тренда.
В отличие от механического, позволяет не только более отчетливо увидеть основную тенденцию развития изучаемого явления, но и получить аналитическую форму изучаемого временного ряда, точнее его основной тенденции.
Эта аналитическая форма получила название трендовой модели. Трендовая модель представляет собой уравнение регрессии, в котором в качестве признака результата выступает уровень изучаемого ряда, а в качестве фактора – время. Уравнение тренда: , где , где y –уровень ряда, t-время. Т.е. уровень ряда есть функция времени.

Графический.
При отображении временного ряда на графике по оси абсцисс – время, по OY значение уровней.
Анализ показателей изменения уровней ДР.
Анализ показателей изменения уровней ДР с учетом свойств известных математических функций. Широко распространен метод конечных разностей. Например, если примерно построенными являются абсолютные приросты (первые разности), а вторые разности равны 0 (ускорение), то в качестве тренда может быть использовано линейное уравнение. Если приблизительно одинаковые вторые разности, а третьи равны 0, то можно использовать полином 2-ой степени, и т.д. Т.е. порядок приблизительно построенных разностей определяет степень полинома.
Формальный выбор тренда с использованием формальных критериев (формул).
Минимальное значение квадрата разности между фактическими и выровненными уровнями.
![]()
![]() - выровненные
уровни.
- выровненные
уровни.
![]() - фактические
уровни.
- фактические
уровни.
Минимальное значение стандартной ошибки или среднеквадратического отклонения.

n – длина ряда
m – число параметров уравнения тренда.
3.3. Минимальное значение средней ошибки аппроксимации
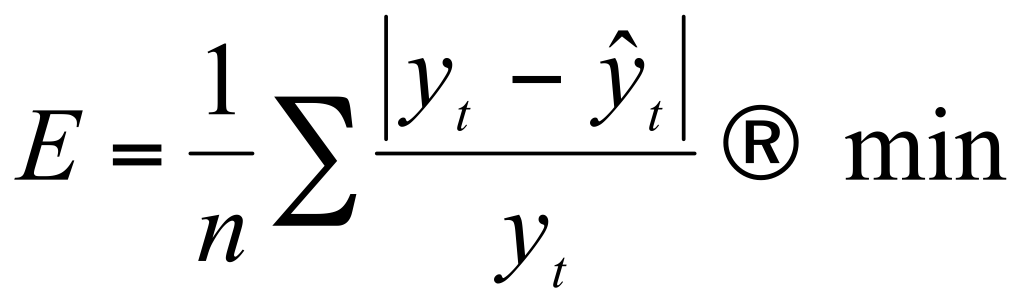
39. Оценка качества модели динамического ряда.
Перечисленные критерии оценивают степень приближения линий тренда к точкам фактических показателей ДР. Поэтому для выбора вида тренда достаточно использовать один из этих критериев.

Наряду с указанными критериями дл выбора формы тренда для последующего программирования max значения коэффициента детерминации или max значение F –критерия Фишера, поскольку эти характеристики отражают степень объясненности вариации результативного признака, в данном случае вариации уровней изучаемого ДР.
Обязательным элементом оценки качества трендовой модели на ее пригодность для прогнозирования является оценка автокорреляции остатков модели.
Остатки – разность между фактическими значениями уровней ряда и значениями, полученными на основе уравнения тренда.
Автокорреляция
– это зависимость остатков каждого
периода от остатков предшествующего
периода.
![]()
наличие автокорреляции в остатках означает присутствие в них тенденции в остатках. Поскольку основная задача трендовой модели – описать основную тенденцию ряда, то сохранение тенденции (автокорреляции) в остатках свидетельствует о плохом качестве полученной модели.
Автокорреляция в остатках может быть оценена через коэффициент автокорреляции, предполагаемый Эзекилем и Фоксом. Он рассчитывается:

Коэффициент автокорреляции изменяется по модулю от 0 до 1. Об отсутствии автокорреляции в остатках говорит величина коэффициента, близкому к 0. Однако, для более объективной оценки наличие или отсутствие автокорреляции в остатках используется специальный критерий Durbin-Watson:

Между
критерием Durbin-Watson
и коэффициентом автокорреляции
существует следующая зависимость:
![]() ,
если
,
если
![]()
Значения
критерия D-W
близкое
к двум будет свидетельствовать об
отсутствии автокорреляции в остатках,
если
![]() Т.е
Т.е
![]()
 .
при полной отрицательной корреляции
остатков D-W=4,
если
.
при полной отрицательной корреляции
остатков D-W=4,
если
![]() ,
т.е. при полной положительной автокорреляции
остатков критерий D-W
=0.
,
т.е. при полной положительной автокорреляции
остатков критерий D-W
=0.
Т.о.
D-W
изменяется
в пределах от
![]() .
Критерий табулирован исходя из числа
уровней ДР и числа параметров уравнения
по таблице находят нижнюю и верхнюю
границы критерия. Если фактическое
значение критерия меньше средней границы
автокорреляция в остатках присутствует.
Если фактическое значение больше верхней
границы, автокорреляция в остатках
отсутствует. Если значение коэффициента
находится между пограничными значениями
– ситуация комментируется как ситуация
неопределенности, требуется дополнительные
исследования.
.
Критерий табулирован исходя из числа
уровней ДР и числа параметров уравнения
по таблице находят нижнюю и верхнюю
границы критерия. Если фактическое
значение критерия меньше средней границы
автокорреляция в остатках присутствует.
Если фактическое значение больше верхней
границы, автокорреляция в остатках
отсутствует. Если значение коэффициента
находится между пограничными значениями
– ситуация комментируется как ситуация
неопределенности, требуется дополнительные
исследования.
![]() -
нижняя.
-
нижняя.![]() - верхняя гр.
- верхняя гр.
Прогнозирование (экстраполяция) на основе трендовых моделей.
Если удается получить качественную модель ДР, то на ее основе может быть осуществлено прогнозирование.
Экстраполяция – продление существующей тенденции в будущие. Может быть осуществлена и на основе показателей изменения уровней ДР, если они примерно постоянны.
Прежде чем приступить к расчету прогноза необходимо обратиться к содержательному теоретическому анализу изучаемого явления или процесса. Поскольку показатели РД и модели характеризуют сложившуюся закономерность в развитие явления, то осуществление прогноза возможно только в условиях уверенности, что в будущем описанная тенденция сохранится.
Трендовая модель – это модель в качестве фактора, которого вступает время.
![]()
Рассчитав параметры a и b для получения прогнозирования достаточно в уравнение тренда подставить порядковый номер года, на который осуществляется прогноз.
Если
![]() ( на 20 лет ДР) нам нужен 21 год, для этого:
( на 20 лет ДР) нам нужен 21 год, для этого:
![]()
Среднегодовой прирост экспорта составляет 0,2 млр.$
Прогноз, полученный на основе уравнения тренда – это та называемый точечный прогноз о полной реализации которого не м.б. и речи. Точечный прогноз д.б. дополнен расчетом доверительных интервалов и указанием доверительной вероятности попадания прогнозируемого показателя в рассчитанный интервал.
Фактическая величина точечного прогноза маловероятна, поскольку тренд описывает только основную тенденцию изучаемого ряда, а уровень ряда кроме трендовой компоненты содержит и др. компоненты, по крайней мере случайную.
Доверительный интервал прогноза рассчитывается на основе показателя, оценивающей степень колеблимости значений фактических уровней вокруг тренда.
