1.6.3 Дерево решения
Обобщим понятие дуги пространства состояний.
Опр. 3. Дугу от вершины типа «ИЛИ» к ее преемнику будем называть унарной связкой (1-связка), k дуг от вершины типа «И» к ее преемникам будем называть k-связкой.
Рассмотрим процесс построения решающего дерева. Выйдем из исходной вершины. Для продолжения движения будем выбирать ровно одну связку. Процесс заканчивается, когда ВСЕ вершины-преемники окажутся терминальными вершинами.
Пространство состояний — частный случай И-ИЛИ графа, т.к. в нем все вершины типа «ИЛИ», и все связки унарные. Для решения «ИЛИ» вершины нужно перейти ровно в одного преемника, поэтому мы получаем путь. Для решения «И» вершины мы должны решить все подзадачи, т.е. перейти в k ее вершин-преемников, поэтому мы получаем дерево. Построение решающего дерева по И-ИЛИ графу — это дело стратегии, т.е. системы управления (глубина, ширина, эвристический поиск). Построим И-ИЛИ граф и выделим в нем дерево решения для нашего примера (рис. 15):
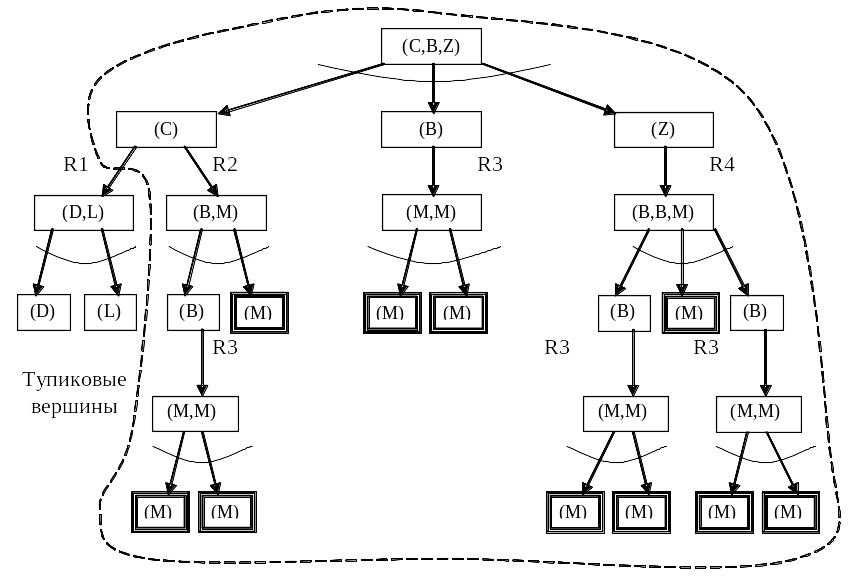
Рисунок 15. «И-ИЛИ» граф для разложимой системы продукций
Штриховой линией обведена та часть И-ИЛИ графа, которая является деревом решения.
Контрольные вопросы.
Что такое системы продукций? Каковы их отличия от иерархической вычислительной системы?
Что такое разложимые системы продукций? Что является представлением задачи, описываемой разложимой системой продукций?
В чем состоит основное отличие И-ИЛИ графа от пространства состояний?
Как построить дерево решения на И-ИЛИ графе?
1.7. Стратегии управления поиском на и-или графах
1.7.1. Представление задачи в виде и-или графов
Для некоторых задач представление в виде И-ИЛИ графа является более естественным, чем в виде пространства состояний. Это задачи, которые разбиваются на взаимно независимые задачи.
Рассмотрим традиционный пример о поиске кратчайшего маршрута от пункта a до пункта z (рис. 16).
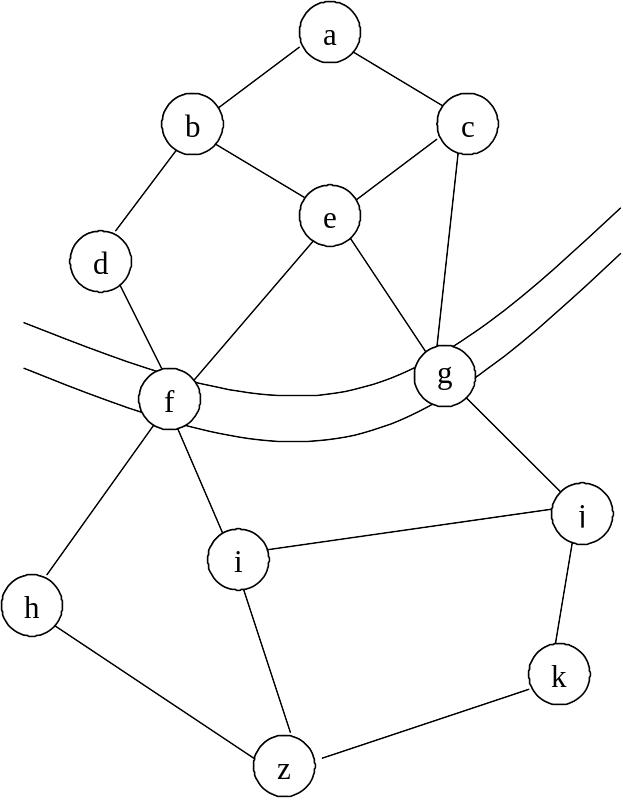
Рисунок 16. Карта дорог для задачи о поиске пути от пункта a до пункта z
Разумеется, эту задачу проще решить с помощью обычного пространства состояний, причем пространство состояний в точности соответствовало бы карте. Попробуем представить ее с помощью разложимой системы продукций. Нашей исходной задачей, или начальной вершиной, является задача «найти путь от a до z» так как f и g — мосты, то попасть из a в z можно либо через пункт f, либо через пункт g. Следовательно, «найти путь из a в z» вершина типа «ИЛИ». Задачи «найти путь от a до z через f» и «найти путь от a до z через g» разбиваются на две подзадачи: «путь от a до моста» и «путь от моста до z». Следовательно, эти задачи являются вершины типа «И». Дальнейшее разбиение можно построить, вводя дополнительные промежуточные пункты. Изобразим часть И-ИЛИ графа на рис. 17:
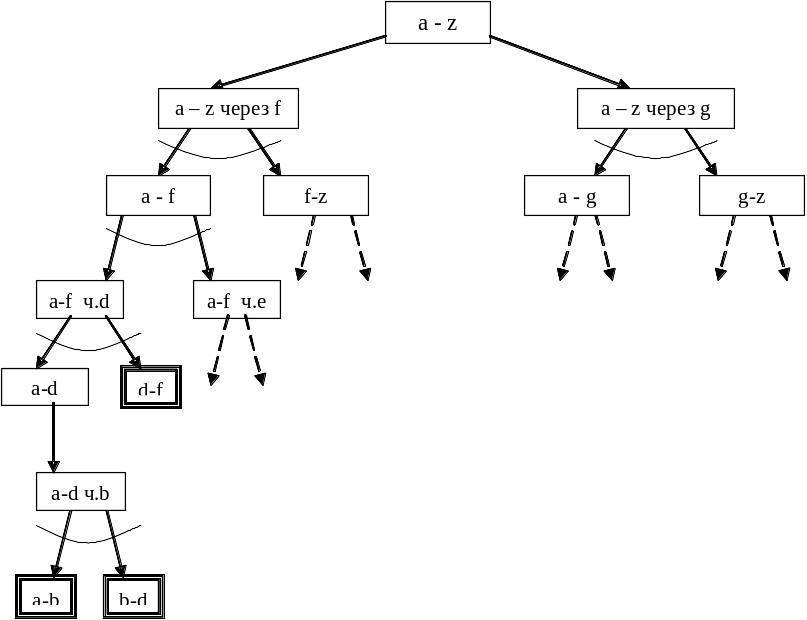
Рисунок 17. Верхняя часть «И-ИЛИ» графа для задачи о мостах
Целевыми вершинами И-ИЛИ графа являются задачи, решаемые непосредственно, т.е. задачи о нахождении пути между вершинами карты, соединенные ребром.
После проведения на этом И-ИЛИ графе какого-либо вида поиска (глубина, ширина, эвристический поиск) будет построено следующее дерево решения (рис. 18):
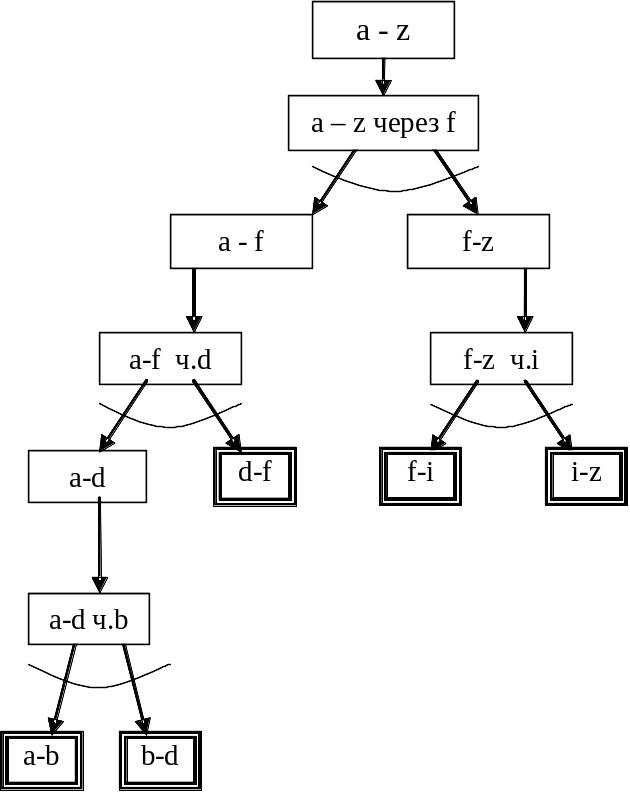
Рисунок 18. Дерево решения задачи о мостах, построенное эвристическим поиском на «И-ИЛИ» графе
Путь от a до z можно восстановить обходом терминальных вершин слева направо: a — b, b — d, d — f, f — i, i — z.