Векторные и комплексные функции действительного аргумента.
Комплексные числа. Алгебраическая, тригонометрическая и показательная формы комплексного числа. Действия над комплексными числами.
Комплексные числа.
Определение.
Комплексным
числом z
называется
выражение
,
где a
и b
– действительные числа, i
– мнимая единица, которая определяется
соотношением:
При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).
Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Определение.
Числа
и
называются
комплексно
– сопряженными.
Определение.
Два комплексных числа
и
называются равными, если соответственно
равны их действительные и мнимые части:
Определение.
Комплексное число равно нулю, если
соответственно равны нулю действительная
и мнимая части.
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.
у
A(a, b)
r b
0 a x
Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.
С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Тригонометрическая форма числа.
Из
геометрических соображений видно, что
.
Тогда комплексное число можно представить
в виде:
Такая форма записи называется тригонометрической формой записи комплексного числа.
При
этом величина r
называется модулем
комплексного
числа, а угол наклона
- аргументом
комплексного
числа.
.
Из
геометрических соображений видно:
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.
Действия с комплексными числами.
Основные действия с комплексными числами вытекают из действий с многочленами.
1) Сложение и вычитание.
2) Умножение.
В
тригонометрической форме:
,
С
случае комплексно – сопряженных чисел:
3)
Деление.
В
тригонометрической форме:
4) Возведение в степень.
Из
операции умножения комплексных чисел
следует, что
В общем случае получим:
,
где n – целое положительное число.
Это выражение называется формулой Муавра.
Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.
Пример. Найти формулы sin2 и cos2.
Рассмотрим
некоторое комплексное число
Тогда
с одной стороны
.
По
формуле Муавра:
Приравнивая,
получим
Т.к.
два комплексных числа равны, если равны
их действительные и мнимые части, то
Получили известные формулы двойного угла.
5) Извлечение корня из комплексного числа.
Возводя в степень, получим:
Отсюда:
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
Показательная форма комплексного числа.
Рассмотрим
показательную функцию
Можно
показать, что функция w
может быть записана в виде:
Данное равенство называется уравнением Эйлера. Вывод этого уравнения будет рассмотрен позднее. (См. ).
Для комплексных чисел будут справедливы следующие свойства:
1)
2)
3)
где m
– целое число.
Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:
Для
комплексно – сопряженного числа
получаем:
Из этих двух уравнений получаем:
Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.
Если
представить комплексное число в
тригонометрической форме:
и
воспользуемся формулой Эйлера:
Полученное равенство и есть показательная форма комплексного числа.
Комплексные функции действительного аргумента: определение, предел, непрерывность, дифференцирование.
Если
каждому действительному числу
по некоторому правилу
поставлено
в соответствие единственное комплексное
число
,
то говорят, что
-
комплексная функция действительного
аргумента.
Так как всякое комплексное число может быть представлено в алгебраической форме, то задание комплексной функции фактически равносильно заданию пары обычных действительных функций.
Графиком комплексной функции действительного аргумента является некоторая кривая на плоскости.
Определение предела непрерывности производной комплексной функции существенно не отличается от соответствующих определений функции действительного аргумента.
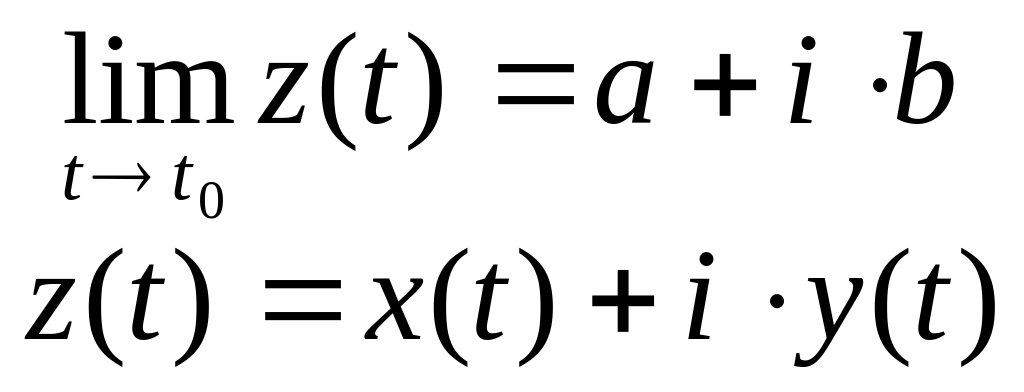
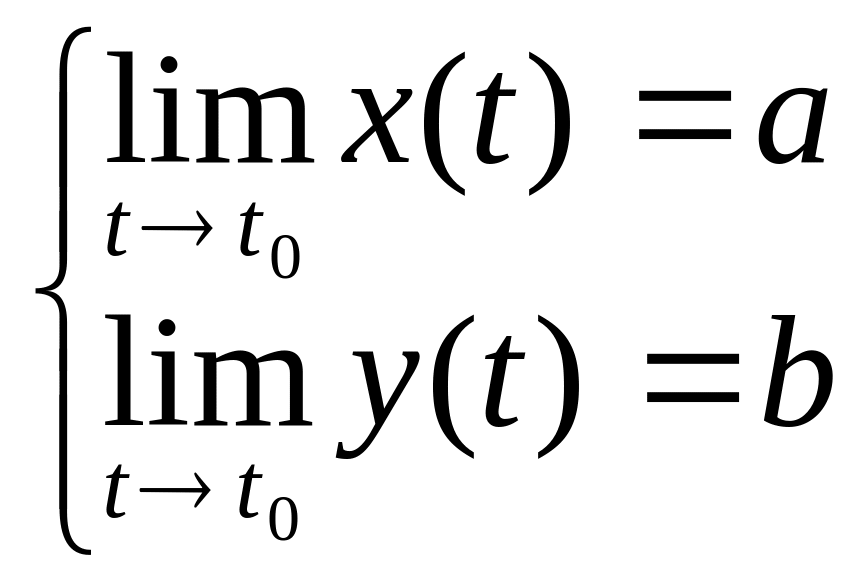
Если
,
то
.
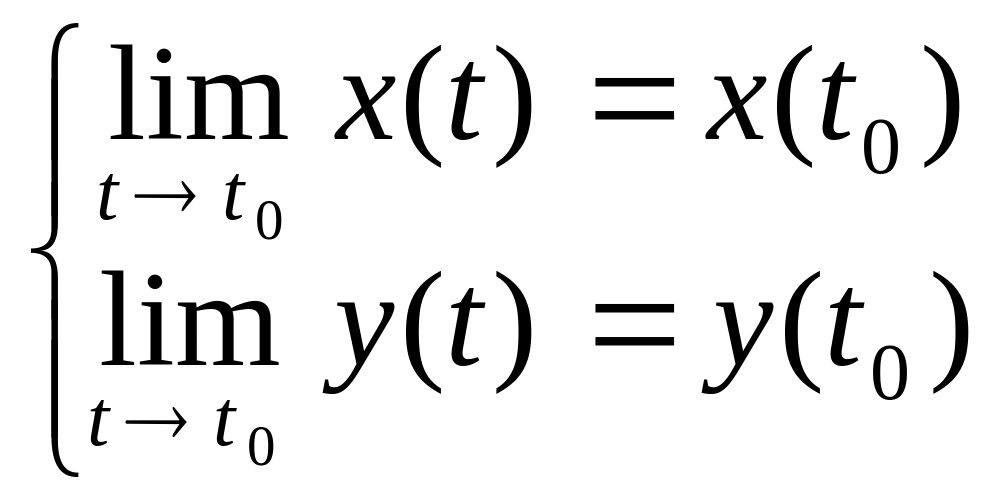Если действительная и мнимая часть функции в точке непрерывны, то и сама функция непрерывна. Если хотя бы один из таких пределов не существует, то предел комплексной функции в точке тоже не существует.
Нахождение производной комплексного переменного ничем не отличается.
Пример.
Найти
производную
в точке
.
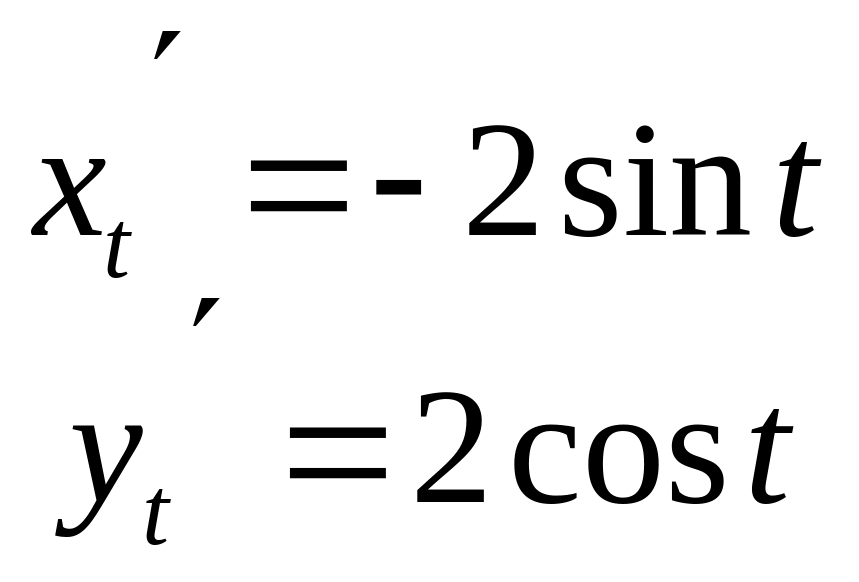
Векторные функции скалярного аргумента: определение, предел, непрерывность, производная.
Векторная функция скалярного аргумента.
z
A(x, y, z)
y
х
Пусть некоторая кривая в пространстве задана параметрически:
x = (t); y = (t); z = f(t);
Радиус-
вектор произвольной точки кривой:
.
Таким
образом, радиус- вектор точки кривой
может рассматриваться как некоторая
векторная функция скалярного аргумента
t.
При изменении параметра t
изменяется величина и направление
вектора
.
Запишем соотношения для некоторой точки t0:
Тогда
вектор
- предел функции
(t).
.
Очевидно, что
,
тогда
.
Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
;
;
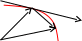
или, если существуют производные (t), (t), f(t), то
Это выражение – вектор производная вектора .
Если имеется уравнение кривой: x = (t); y = (t); z = f(t);
то
в произвольной точке кривой А(xА,
yА,
zА)
с радиус- вектором
можно провести
прямую с уравнением
Т.к. производная - вектор, направленный по касательной к кривой, то
.
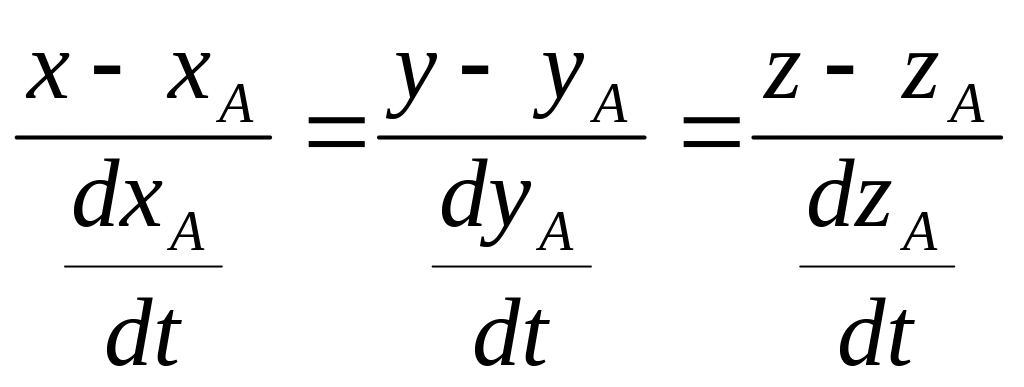Свойства производной векторной функции скалярного аргумента.
1)
2)
,
где
= (t)
– скалярная функция
3)
4)
Определение. Векторной функцией действительного аргумента называется правило, которое каждому действительному числу ставит в соответствие единственный определенный вектор.
Комплексное число – пара чисел, а векторная функция – вектор в пространстве.
Различным значениям аргумента могут соответствовать разные значения вектор-функции.
Линия, которая описывается в пространстве при непрерывном изменении аргумента, называется годографом вектор-функции скалярного аргумента.
С физической точки зрения годограф вектор-функции можно рассматривать как траекторию движущейся в пространстве материальной точки.
Для аналитического описания вектор-функции и ее годографа выберем декартовую прямоугольную систему координат.
параметрическое
задание годографа, равносильно заданию
трех действительных аргументов.
-
конец вектора
при известном
.
Понятие предела.
Вектор-функция
непрерывна в
,
если предел этой функции в точке равен
значению вектор-функции в этой точке.
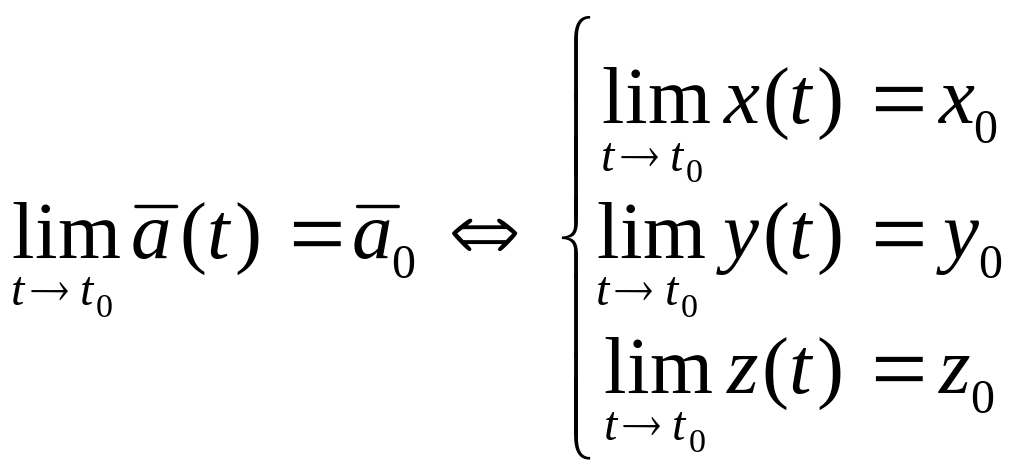
Если предел в точке равен значению функции в точке , то говорят, что вектор-функция в точке непрерывна.
Для того, чтобы вычислить предел вектор-функции в точке, достаточно найти пределы координат этой функции.
С
практической точки зрения, если
вектор-функция
имеет
,
то
