67. Определение среднего предела текучести металла в очаге деформации (метод а.А. Динника)

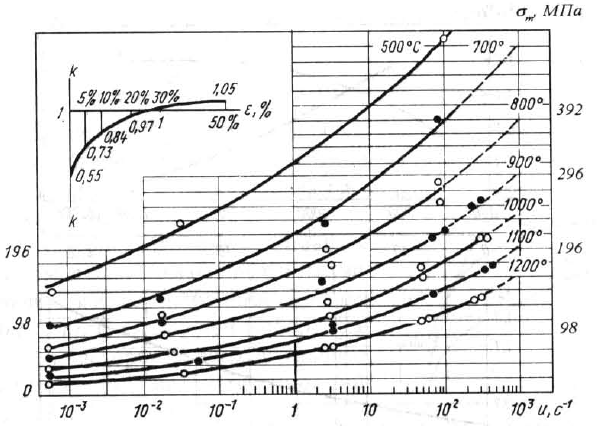
При горячей прокатке основными факторами влияющие на определение предела текучести является степень деформации, скорость деформации, температура, природа материала. Определяются на пластометрах.

На графиках А.А. Динника (добавли 15 сталей к уже имеющимся графикам P.M. Cook) основные кривые соответствуют обжатию ε=30%, корректировку данных по фактическому обжатию проводят при помощи вспомогательного графика, из которого берут поправочный коэффициент К: , где - предел текучести при обжатии 30%.

t=600-1200^оС, u=10^-2-10^-3 , ε = 0-50

68. Определение среднего предела текучести металла в очаге деформации по методу термомеханических коэффициентов (метод в.И. Зюзина).

Средний предел текучести в очаге деформации для конкретных условий горячей прокатки определяется из выражения , где - предел текучести материала полученный в опытах при t=1000^оС, u=10^-1с, ε = 0,1, - термомеханические коэффициенты, учитывающие соответственно степень и скорость деформации, температуру. В литературе приведены базисные значения пределов текучести для 44 марок сталей и 20 цветных металлов и сплавов. Коэффициенты определяют из специальных графиков, построенных для каждого металла.

69. Определение среднего предела текучести металла в очаге деформации при холодной прокатке.

При холодной прокатке основным фактором, влияющим на предел текучести, является деформационное упрочнение или наклеп. При выборе прежде всего необходимо учитывать суммарное обжатие получены при холодной деформации. Предел текучести определен по кривым упрочнения. Третьяков (см рисунок)

, где - предел текучести не наклепанного горячекатаного (или отожженного) металла. ε- суммарное относительное обжатие, %, а, n – эмпирические коэффициенты зависящие от химического состава.

.

Для сильно наклепанного металла

Для расчетов применяется средний предел текучести , где пределы текучести в сечении входа и в сечении выхода из очага деформации. Погрешность данного метода заключается в том, что в реальных условиях предел текучести растет неравномерно. В реальных условиях для повышения прочности используют подход по среднему относительному обжатию , где о,1- суммарные относительные обжатие до и после пропуска металла через валки.

Дополнительные факторы влияющие на предел текучести: 1) скорость деформации: на разрывной машине скорость деформации u 10^-3-10^-2 c^-1, на современных промышленных станах скорость деформации 10²-10³ с^-1, т.е. Δu = 10⁴-10⁶ В этом случае предел текучести возрастает на 30-40%. 2) схема нагружения: на разрывной машине – растяжение, а на стане – сжатие. Доказано, что при сжатии предел текучести выше на 10%, т.е. погрешность +10%. 3) температура: реальная температура прокатки 200-250. Определение приращения температуры в общем случае приращения температур происходит диссипация энергии, за счет трения на контактных поверхностях.

70. Дифференциальное уравнение равновесия продольных сил.

Вывод большинства теоретических формул для определения усилия прокатки основан на решении дифференциального уравнения равновесия продольных сил приложенных к металлу в очаге деформации.

Р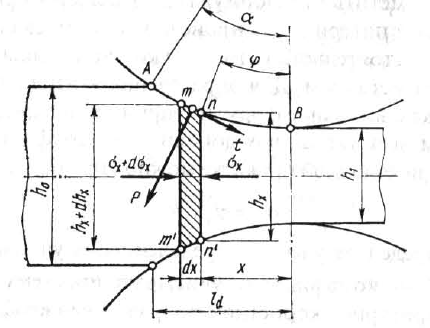 ассмотрим условие равновесия элементарного объема mnm’n’ при следующих допущениях: напряжение в любом поперечном сечении по высоте распределяется равномерно; деформация является плоской, т.е. прокатка без уширения и напряжение по ширине полосы не изменяется

Грань nn’: , где сигма – продольное напряжение, hx и b – высота и ширина полосы в сечении

Грань mm’:

Определяем продольные силы, создаваемые контактными напряжения P и t на площадках mn и m’n’

Принимаем, что элементарный объем выделен в зоне отставания, тогда сила t втягивает металл в очаг деформации. Находим горизонтальные составляющие от действия силы P

Где – длина площадок mn и n’m’ по касательной

От действия t

Находим и записываем уравнение равнодействия на горизонтальной оси

Σх=0