1.3. Свойства напряжений внутренних сил.

Д ля исследования напряжений внутренних сил в жидкости установим связь между напряжениями, действующими на произвольно ориентированную площадку и три взаимно перпендикулярные площадки, проходящие черезо одну точку. Для этого мысленно выделим в движу-щейся жидкости элементарную (ма-лую) жидкую ча-стицу в форме тетраэдра объемом V (рис.3).

На гранях тетраэдра изобра-жены не поверх-ностные силы, а напряжения этих сил, направленные произвольным образом к соответствующим граням. Индекс у вектора напряжения характеризует ориентировку площадки, т.е. нормаль. За положительное направление нормали принимается внешнее по отношению к выделенному жидкому объему. Ускорение центра тяжести частицы обозначим ; напряжение массовых сил - .

Уравнение движения этой элементарной частицы в векторной форме основано на втором законе Ньютона: произведение массы тела на его ускорение равно сумме всех действующих на него сил

,

или, с учетом напряжений массовых сил и напряжений поверхностных сил, действующих на грани тетраэдра со стороны отброшенной внешней жидкости

, (1.6)

где S_x, S_y и S_z – площади граней тетраэдра, перпендикулярных соответствующим осям координат; , , , - векторы напряжений в центре площадок, обозначения которых соответствуют направлению нормалей к ним; знаки «минус» перед последними тремя слагаемыми означают, что нормали к соответствующим площадкам направлены противоположно осям координат.

Из аналитической геометрии известно, что

(1.7)

Разделим обе части уравнения (1.6) на S_n и используем (1.7)

(1.8)

Для получения связи между напряжениями в точке, устремим объем тетраэдра к нулю, стягивая его в точку к началу координат. При этом , а следовательно, связь между напряжениями запишется в виде

. (1.9)

Проектируя это векторное уравнение на оси координат, получим

;

; (1.10)

,

где первый индекс при проекциях напряжений соответствует ориентации площадки, на которой действует напряжение, а второй – оси, на которую оно проектируется.

При этом скалярные величины p_xx, p_yy, p_zz представляют собой нормальные напряжения, а p_xy, p_xz,... – касательные напряжения, действующие в соответствующих площадках.

Касательные напряжения в дальнейшем будем обозначать буквой  (_xy, _yz, _xz) – как показано на рис.4. На этом рисунке изображены нормальные и касательные напряжения, действующие на три взаимно перпендикулярные грани параллелепипеда, выделенного в жидкости.

Применяя теорему моментов относительно начала координат для изображенных напряжений, нетрудно доказать свойство взаимности касательных напряжений, состоящее в том, что

; ; . (1.11)

Кроме свойства взаимности, существуют и другие свойства напряжений в жидкости. Касательные напряжения  возникают только при движении реальной вязкой жидкости. При движении невязкой жидкости они равны нулю. В покоящейся жидкости касательные напряжения также равны нулю, так как жидкости не обладают свойством трения покоя.

Отметим два свойства нормальных напряжений. Первое свойство: при отсутствии касательных напряжений, т.е. когда , нормальные напряжения не зависят от ориентации площадки

. (1.12)

З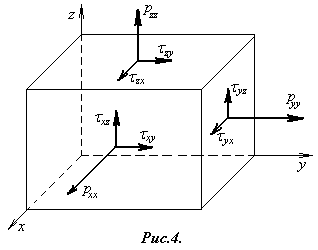 ависимость (1.12) выполняется при покое вязкой жидкости, а также при движении и покое невязкой жидкости.

Второе свойство: При отсутствии касательных напряжений в жидкости могут проявляться только сжимающие (отрицательные) усилия, которые называются давлениями.

Давлением в жидкости при отсутствии касательных напряжений называют величину нормальных напряжений, взятую с обратным знаком:

, (1.13)

откуда следует, что величина давления не зависит от ориентации площадки.