
- •В.В. Киричевський, н.М. Д’яченко інтегральне числення
- •6.050100 „Економічна кібернетика”
- •1. Неозначений інтеграл
- •1.1. Первісна і неозначений інтеграл
- •1.1.1. Основні властивості неозначеного інтегралу.
- •1.1.2. Таблиця основних інтегралів.
- •1.2. Основні методи інтегрування
- •1.2.1. Безпосереднє інтегрування.
- •1.2.2. Метод підстановки.
- •1.2.2.1. Частковий випадок: метод інтегрування внесення під диференціал.
- •1.2.2.2. Загальний випадок.
- •1.2.3. Інтегрування частинами.
- •1.3. Інтегрування раціональних функцій
- •1.4. Інтегрування тригонометричних функцій
- •1.5. Інтегрування ірраціональних функцій
- •2. Означений інтеграл
- •Поняття означеного інтегралу Римана та його властивості. Геометричний зміст означеного інтегралу
- •2.2. Економічний зміст означеного інтегралу
- •2.3. Обчислення означених інтегралів.
- •3. Застосування означеного інтегралу
- •3.1. Застосування означеного інтегралу в геометрії
- •3.1.1. Обчислення площ плоских фігур.
- •3.1.2. Обчислення довжин плоских дуг
- •3.1.3. Обчислення об’ємів тіл обертання
- •3.2. Застосування означеного інтегралу в економіці
- •4. Невласні інтеграли
- •5. Узагальнення поняття інтегралу
- •5.1. Визначення подвійного інтегралу та його властивості
- •5.2. Обчислення подвійних інтегралів
- •5.3. Геометричний зміст подвійного інтегралу
- •Типове індивідуальне завдання
- •Список літератури
- •Питання, що виносяться на самостійне вивчення
- •Питання, що виносяться на іспит і на колоквіум
- •Інтегральне числення
- •6.050100 „Економічна кібернетика”
2.2. Економічний зміст означеного інтегралу
Література
[4 c.
286-287].
Нехай функція
![]() описує зміну продуктивності деякого
виробництва залежно від часу. Знайдемо
обсяг продукції
описує зміну продуктивності деякого
виробництва залежно від часу. Знайдемо
обсяг продукції
![]() ,
що вироблено за проміжок часу
,
що вироблено за проміжок часу
![]() .
.
Відмітимо,
що за умови незмінності продуктивності
з часом (тобто
![]() )
обсяг продукції
)
обсяг продукції
![]() ,
яка виготовлена за деякий проміжок часу
,
яка виготовлена за деякий проміжок часу
![]() ,
визначається формулою
,
визначається формулою
![]() .
В загальному випадку здійснюється
наближена рівність
.
В загальному випадку здійснюється
наближена рівність
![]() ,
де
,
де
![]() ,
яка стає тим більш точною, чим менше
,
яка стає тим більш точною, чим менше
![]() .
.
Розіб’ємо відрізок на проміжки часу
![]() .
.
Для
величини обсягу продукції
![]() ,
що вироблено за проміжок часу
,
що вироблено за проміжок часу
![]() ,
маємо
,
маємо
![]() ,
де
,
де
![]() ,
,
![]() .
Тоді
.
Тоді
![]()
![]() .
.
Якщо
![]() прагне до нуля, то наближена рівність
стає все більш точною, тому
прагне до нуля, то наближена рівність
стає все більш точною, тому
![]() .
.
Враховуючи визначення означеного інтегралу, отримаємо
![]() ,
,
тобто,
якщо
![]() ‑ продуктивність праці в момент часу
‑ продуктивність праці в момент часу
![]() ,
то
‑ це обсяг продукції, що випускається
за проміжок часу
.
,
то
‑ це обсяг продукції, що випускається
за проміжок часу
.
З
наведеного випливає, що обсяг продукції,
що виробляється за проміжок часу від
![]() до
до
![]() дорівнює
дорівнює
|
1. За
функцією продуктивності праці
![]() [дет/год], знайти скільки деталей зробить
робітник за другу половину робочого
дня.
[дет/год], знайти скільки деталей зробить
робітник за другу половину робочого
дня.
Другій
половині робочого дня відповідає
проміжок часу від
![]() [год.]
до
[год.]
до
![]() [год.].
За цей час робітник виготовить
[год.].
За цей час робітник виготовить

![]() [дет].
[дет].
2.3. Обчислення означених інтегралів.
(№Д2242)

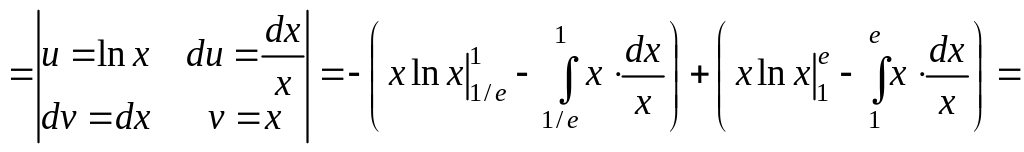

(№Д2247)
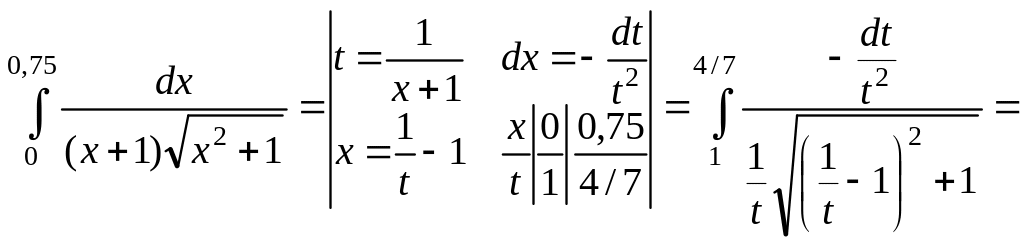


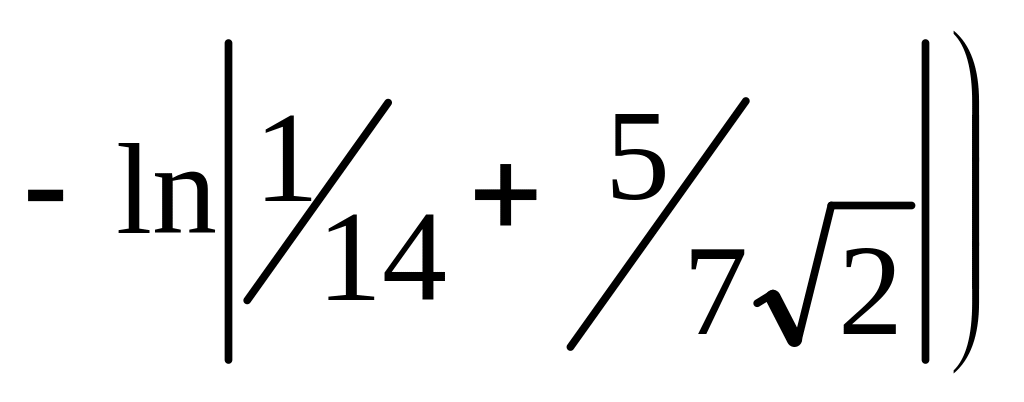
 .
.(№Д2246)


 .
.
Задача 2.2. Отримати формулу
|
(2.1) |
3. Застосування означеного інтегралу
3.1. Застосування означеного інтегралу в геометрії
3.1.1. Обчислення площ плоских фігур.
П
Рис.
3.1.

![]() ,
,
![]() ,
де
,
де
![]() ,
відрізками прямих
,
(рис. 3.1), обчислюється за формулою
,
відрізками прямих
,
(рис. 3.1), обчислюється за формулою
|
Я
Рис. 3.2.
Рис.
3.3.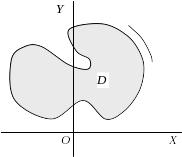
![]() ‑ параметричне рівняння кривої,
обидві координатні функції якої
неперервні разом із своєю похідною на
,
крім того крива є замкненою, пробігає
проти руху стрілки годинника, обмежує
зліва від себе фігуру
з площею
‑ параметричне рівняння кривої,
обидві координатні функції якої
неперервні разом із своєю похідною на
,
крім того крива є замкненою, пробігає
проти руху стрілки годинника, обмежує
зліва від себе фігуру
з площею
![]() (рис. 3.2), тоді
(рис. 3.2), тоді
|
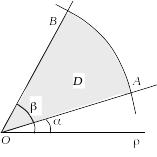
Площа
сектора OAB (рис. 3.3), що обмежений
неперервною кривою
![]() ,
заданою в полярній системі координат,
і двома півпрямими
,
заданою в полярній системі координат,
і двома півпрямими
![]() і
і
![]() (
(![]() )
дорівнює
)
дорівнює
|
Не будемо зупинятися на строгому математичному визначенні квадрованих фігур, але зазначимо, що всі області, що розглянуті вище з наведеними для них формулами обчислення площ є квадрованими плоскими фігурами, тобто фігурами, що мають площу.
(
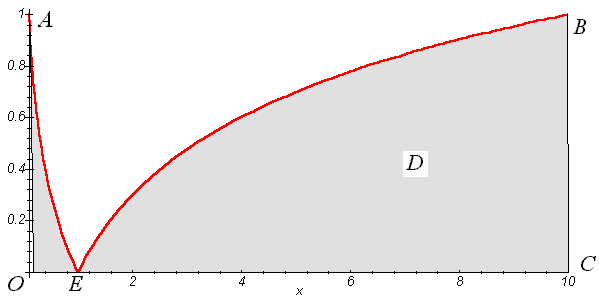
Рис. 3.4.
№Д2400 Знайти площу фігури, що обмежена кривими
![]() .
.
На рис.
3.4. зображено дану фігуру
(OAEBC).
Вона є криволінійною трапецією, площа
якої дорівнює
![]()
![]() .
Цей інтеграл будемо обчислювати частинами
аналогічно прикладу 1 пункту 2.2:
.
Цей інтеграл будемо обчислювати частинами
аналогічно прикладу 1 пункту 2.2:



![]()
![]()
(№Д2400.2) Знайти площу фігури, що обмежена кривими
 ,
,
 ,
,
 (
( ).
).
Дану
фігуру
зображено на рис. 3.5. Її площу можна
обчислювати двома способами. Перший
спосіб цікавий з методичного погляду
і він полягає в необхідності розбиття
області на дві частини віссю ординат.
Ліва з цих частин є криволінійною
трапецією, що обмежена віссю абсцис,
графіком функції
і вертикальними прямими
![]() і
і
![]() .
Права частина обмежена знизу гілкою
синусоїди, що виражається через обернену
тригонометричну функцію за формулою
.
Права частина обмежена знизу гілкою
синусоїди, що виражається через обернену
тригонометричну функцію за формулою
![]() ,
а зверху іншою гілкою ‑
,
а зверху іншою гілкою ‑
![]() ,
а також вертикальними прямими
і
,
а також вертикальними прямими
і
![]() .
Площа області
буде дорівнювати сумі площ двох утворених
частин, тому
.
Площа області
буде дорівнювати сумі площ двох утворених
частин, тому
Рис. 3.5.![]()

Перший інтеграл обчислюється, як інтеграл від степеневої функції, а другий ‑ частинами. Не будемо зупинятися на його обчисленні і запропонуємо це зацікавленому читачеві.
Наведемо
більш простий другий спосіб. Оскільки
ця фігура зліва обмежена гілкою (правою)
параболи, справа – синусоїдою, а також
горизонтальними прямими
і
![]() ,
то її площу можна обчислити також за
формулою
,
то її площу можна обчислити також за
формулою
![]() ,
де
,
де
![]() ,
,
![]() ,
,
![]() ,
рівняння правої гілки параболи, в якому
x
виражене через y,
утворює рівняння кривої
,
рівняння правої гілки параболи, в якому
x
виражене через y,
утворює рівняння кривої
![]() .
Якщо
,
то звідси
.
Якщо
,
то звідси
![]() .
Знак „+” дає праву гілку параболи, а
„‑”
– ліву, тому
.
Знак „+” дає праву гілку параболи, а
„‑”
– ліву, тому
![]() .
Таким чином,
.
Таким чином,
![]()
Для спрощення студентові задачі з виконання типових завдань на рис. 3.7-3.9 наведено графіки деяких функцій, що задані параметрично.
(№Д2414) Обчислимо площу петлі, що зображена на рис. 3.9:
 .
.
Щоб
дізнатися, яким значенням параметра
![]() відповідає петля, потрібно знайти точку
відповідає петля, потрібно знайти точку
![]() самоперетину графіку цієї функції і
два
самоперетину графіку цієї функції і
два
значення
![]() і
параметру
,
що їй відповідають, тобто
і
параметру
,
що їй відповідають, тобто
![]() .
.
У
а
б
в
Рис.
3.6.
Графік розгортки круга
а)
Рис.
3.7.
Графік циклоїди
Рис.
3.8.
Графік астроїди Рис. 3.9.
Графік функції

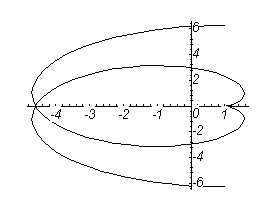
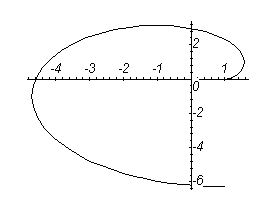
![]() при
при![]() ;
б)
;
б)
![]() ,
в)
,
в)
![]()
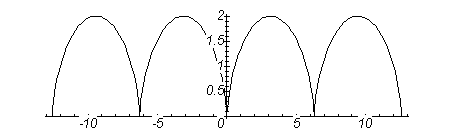
![]() при
при


![]() при
.
Петля при
при
.
Петля при
![]()
![]()
![]() .
.
(№Д2429) Зводячи рівняння до параметричного виду, знайти площу фігури, що обмежена кривою
 .
.
Треба
увести таку тригонометричну параметризацію,
яка після підстановки у ліву частину
виділяє в ній тригонометричну одиницю.
Такою параметризацією буде
![]() .
При зростанні параметра
від 0 до
.
При зростанні параметра
від 0 до
![]() крива робить повний обхід проти руху
стрілки годинника і замикається в точці
крива робить повний обхід проти руху
стрілки годинника і замикається в точці
![]() .
Ця крива називається астроїдою; при
.
Ця крива називається астроїдою; при
![]() її графік зображено на рис. 3.8.
Обчислимо її площу
її графік зображено на рис. 3.8.
Обчислимо її площу
![]() .
.
Перший спосіб обчислення інтегралу. Отриманий інтеграл має суму показників степенем обох тригонометричних функцій парну, тому його можна обчислити з використанням формули зниження степеня і формули синуса подвійного кута:

Звідки одержимо
![]()
![]() .
.
Другий спосіб обчислення інтегралу. Для застосування формули (2.1) зауважимо, що в силу симетрії даної функції відносно прямих
![]() отримаємо
отримаємо
![]() ,
тому
,
тому

![]()
Д
Рис.
3.10.
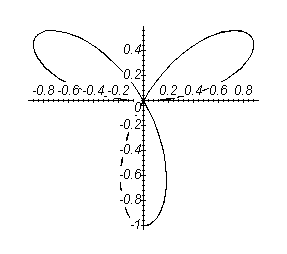
Графік кардіоїди Рис. 3.11.
Графік трилисника
а б
Рис.
3.12.
Графіки лемніскат а)

![]()
![]()
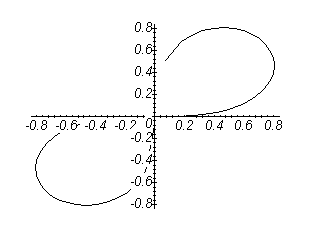

![]() ,
б)
,
б)
![]()
(№Д2419) Обчислити площу фігури, що обмежена кардіоїдою
 .
.
При
графік кардіоїди зображено на рис. 3.10.
Графік даної функції обмежує симетричну
відносно вісі абсцис фігуру, тому площа
частини цієї фігури, що відповідає зміні
полярного кута
![]() від 0 до
від 0 до
![]() ,
дорівнює половині площі усієї цієї
фігури, тобто
,
дорівнює половині площі усієї цієї
фігури, тобто
![]()
![]()
6. (№Д2428) Переходячи до полярних координат, знайти площу кривої
![]() .
.
Нехай
![]() ,
тоді рівняння кривої перепишеться у
вигляді
,
тоді рівняння кривої перепишеться у
вигляді
![]() ,
тобто
,
тобто
![]() (при
графік даної лемніскати зображено на
рис. 3.12 а). Щоб дізнатися про межі зміни
полярного кута
потрібно розв’язати нерівність
(при
графік даної лемніскати зображено на
рис. 3.12 а). Щоб дізнатися про межі зміни
полярного кута
потрібно розв’язати нерівність
![]() .
У даному випадку вона рівносильна
нерівності
.
У даному випадку вона рівносильна
нерівності
![]() ,
розв’язок якої має вигляд
,
розв’язок якої має вигляд
![]() .
Щоб не потрапити на повторний оберт
навколо кривої потрібно взяти
.
Щоб не потрапити на повторний оберт
навколо кривої потрібно взяти
![]() і
і
![]() ,
тоді
,
тоді
![]() .
Фігура симетрична відносно початку
координат, тому
.
Фігура симетрична відносно початку
координат, тому
![]()

 .
.