1.2.2.2. Загальний випадок.

1. (№Д1776) .

2. (№Д1777) .

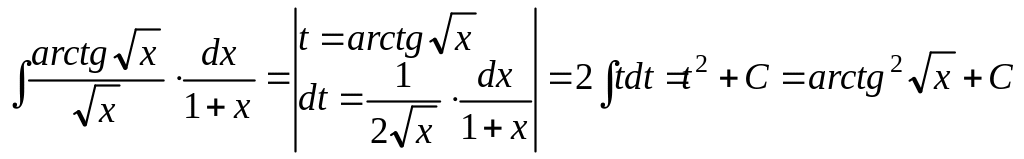За допомогою тригонометричних замін обчислюють інтеграли, що містять такі ірраціональності:

1) (після заміни отримаємо );

2) (після заміни отримаємо );

3) (після заміни отримаємо ) та інші.

Наприклад:

3.

.

Оскільки , а , то , тому

.

4.

Оскільки , то , тому модуль відкривається із знаком „+”, звідки отримаємо

.

Далі скористаємось формулою і одержимо

.

1.2.3. Інтегрування частинами.

Теорема 1.3. Якщо функції і диференційовані на і існує на неозначений інтеграл , тоді існує інтеграл і має місце формула

.

Основні класи функцій, що інтегруються частинами.

	Види інтегралів	Перша підінтегр. функція	Друга підінтегр. функція	Заміни	Зауваження
А)	та звідні до них	- многочлен,			Формула інтегрування частинами застосовується разів
Б)	або та звідні до них.	- дробово-лінійна функція, зокрема многочлен		, відповідно (або методом підстановки , відповідно )	Інтегрувати частинами стільки разів, доки підінтегральна функція буде містити
В)	, та звідні до них				Двічі інтегрувати частинами (див. приклад 3)
Г)	інші

1. Обчислимо інтеграл, що відноситься до класу А.

.

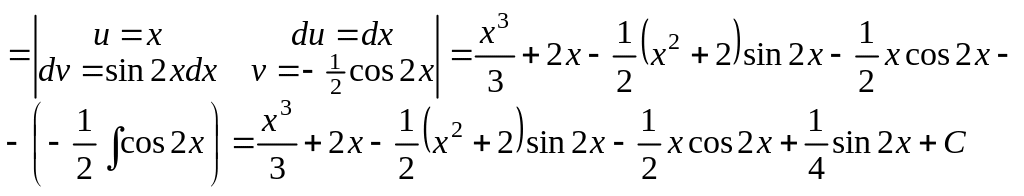2. Тепер обчислимо інтеграл із класу Б (№Д1813).

.

3. Позначимо . Цей інтеграл потрібно двічі інтегрувати частинами, кожен раз уводячи споріднені заміни, тобто або кожен раз експоненціальну функцію позначати через , а тригонометричну, помножену на через , або навпаки:

.

Маємо: , звідки одержимо

.

Аналогічно можна отримати

.

4. (№Д1808) Інтеграл типу Б

.

Згідно до таблиці інтеграл виражається через , в якому опущено у відповіді модуль, тому що дана підінтегральна функція має множину визначення .

5. (№Д1820) Інтеграл типу Г.

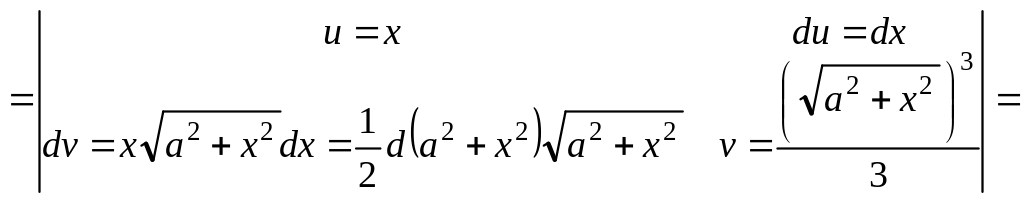
Звідки одержимо

.

Зауважимо, що цей інтеграл також можна інтегрувати тригонометричними або гіперболічно-тригонометричними підстановками.

Зауваження 1.1. Не всі елементарні функції інтегруються в елементарних функціях. До таких функцій відносяться

1. інтеграл Пуассона (інтеграл помилок) , що використовується в теорії ймовірностей, в статистичній фізиці, теорії теплопровідності і дифузії,

2. інтеграли Френеля , що використовується в оптиці,

3. інтегральний логарифм ,

4. інтегральні косинус і синус .

В наступному параграфі ми розглянемо методи інтегрування раціональних функцій, які завжди інтегруються в елементарних функціях. Після цього перейдемо до деяких інтегралів від тригонометричних і ірраціональних функцій, інтегрування яких можна здійснювати безпосередньо або через раціоналізуючу заміну.