1.3 Численное интегрирование в Mathcad

Численное интегрирование – достаточно простая вычислительная операция. Оно реализовано в виде соответствующего оператора MathCAD.Результатом численного интегрирования является некоторое число – значение определенного интеграла.

Чтобы вычислить определенный интеграл, следует написать его обычную математическую форму:

Решить определенный интеграл можно следующими приближенными методами:

Метод прямоугольников

Главная идея этого способа основана на простых геометрических соображениях, а именно определенный интеграл, который есть площадь криволинейной трапеции. Он вычисляется как сумма площадей элементарных прямоугольников.

Метод левых прямоугольников

Отрезок интеграла 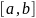разбивается на n-элементарных отрезков равной длины ,

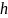Пример метода левых прямоугольников на рисунке 7.

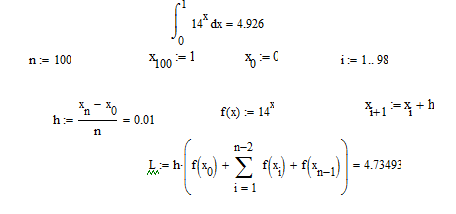
Рис. 7. Метод левых прямоугольников.

Метод правых прямоугольников.

Отрезок интеграла разбивается на n-элементарных отрезков равной длины

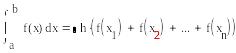
Пример метода правых прямоугольников на рисунке 8.

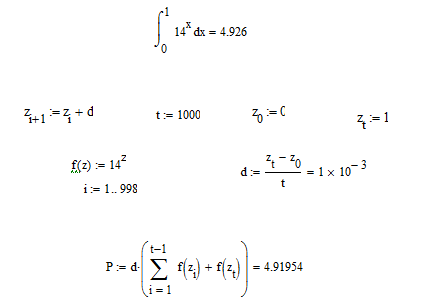
Рис. 8. Метод правых прямоугольников.

Метод средних прямоугольников

Отрезок интеграла разбивается на n-элементарных отрезков равной длины

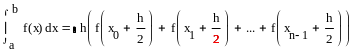
Пример метода средних прямоугольников на рисунке 9.

Метод трапеций

В методе трапеций элементы криволинейной трапеции заменяются прямоугольными трапециями, в результате чего получаем приближенный способ нахождения определенного интеграла.

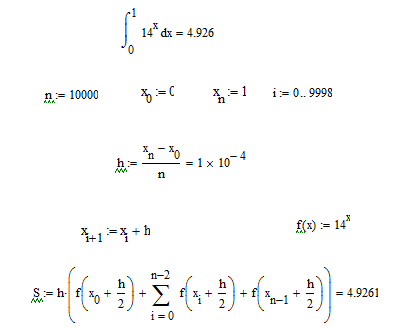
Рис. 9. Метод средних прямоугольников.

Пример метода трапеций на рисунке 10.

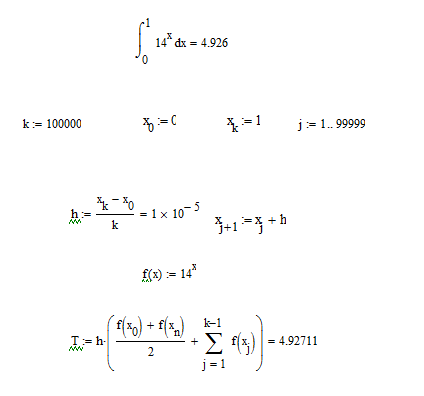
Рис. 10. Метод трапеций.

Метод Симпсона

В данном методе отрезок интеграла разбивается не на n элементарных отрезков, а на n пар элементарных отрезков.

Пример метода Симпсона на рисунке 11.

Рис. 11. Метод Симпсона.

Глава 2. Методы решения нелинейных уравнений

Все функции, которые не являются алгебраическими называются трансцендентными (нелинейными). Все рассмотренные методы решения нелинейных алгебраических уравнений представляют собой итерационные процедуры, последовательно уточняющие значение корня по некоторому алгоритму или итерационной формуле.

2.1 Метод Хорд

Пусть − абсциссы концов хорды, − уравнение прямой, содержащей хорду. Найдем коэффициенты и из системы уравнений:

.

Вычтем из первого уравнения второе:

, затем найдем коэффициенты и :

, тогда

.

Уравнение принимает вид:

Таким образом, теперь можем найти первое приближение к корню, полученное методом хорд:

Теперь возьмем координаты и и повторим все проделанные операции, найдя новое приближение к корню. Повторять операцию следует до тех пор, пока не станет меньше или равно заданному значению погрешности.

Пример метода хорд на рисунке 12.

Рис.12. Метод хорд.

2.2 Метод Ньютона (касательных)

В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.

Формула итераций этого метода имеет вид:

Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения , а затем использовать это значение на каждой последующей итерации:

При таком выборе в точке выполнено равенство:

и если отрезок, на котором предполагается наличие корня и выбрано начальное приближение , достаточно мал, а производная непрерывна, то значение будет не сильно отличаться от и, следовательно, график пройдёт почти горизонтально, пересекая прямую , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.

Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число следует выбрать равным

Пример метода Ньютона(касательных) на рисунке 13.

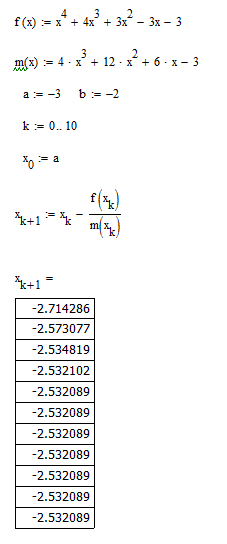
Рис. 13. Метод Ньютона (касательных).