1.2 Решение уравнений линейной алгебры в Mathcad

Решение уравнений вида f(x)=0

Для нахождения корня уравнения вида 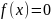следует использовать встроенную в систему функцию root. Эту функцию целесообразно использовать для решения трансцендентных уравнений, т.е. тех уравнений, которые не имеют аналитических решений.

Рассмотрим следующий пример: необходимо определить, при каких значениях переменной x функция обращается в ноль.

Для решения данной задачи вначале следует задать приближенное значение переменной:

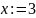
После этого, воспользовавшись встроенной функцией root, можно определить переменную, в которой будет содержаться точное значения корня функции:

Далее это значение можно вывести на рабочий лист:

Точность вычислений задается системной переменной TOL. По умолчанию переменная TOL имеет значение, равное 0,001.

Поиск корней многочлена

Для отыскания всех корней полинома следует использовать встроенную функцию polyroots.

Для применения этой функции следует определить полином:

Чтобы отыскать корни полинома, также следует указать вектор коэффициентов полинома, для чего следует воспользоваться командой Polynomial Coefficients меню Symbolic. В результате выполнения этой команды будет вычислен столбец, содержащий коэффициенты полинома.

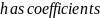
Далее следует определить вектор коэффициентов и вычислить корни полинома:

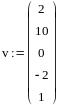
В результате функция возвращает все корни полинома.

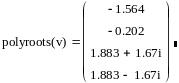
Решение системы линейных уравнений

Для решения систем линейных уравнений используется внутренняя функция lsolve.

Пусть дана система уравнений:

Для ее решения следует определить матрицу коэффициентов, которая не должна быть вырожденной:

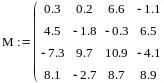
а также указать вектор свободных коэффициентов:

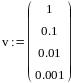
Решение:

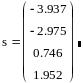
Хорошей альтернативой решению систем в матричной форме является так называемый solve block (Блок решения). Он удобен тем, что при его использовании уравнения записываются не в матричной, а в обычной форме, а также тем, что позволяет решать нелинейные уравнения и вводить ограничительные условия для определяемого решения. Блок решения применяется как для нахождения численного решения, так и для отыскания решения в символьном виде.

Синтаксис Блока решения:

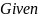
Уравнения

Ограничительные условия

– возвращает значение одной

или ряда переменных для точного решения

– переменные, которые надо найти.

Последовательность действий при численном решении:

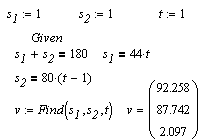
Задаем начальные (стартовые) значения для искомых переменных.

Заключаем уравнения в блок решения, начинающийся ключевым словом и заканчивающийся ключевым словом

Если после слова ввести знак равенства [=], Mathcad выдаст численное решение.

При символьном решении не надо вводить начальные значения, а после ключевого слова вместо знака равенства следует ввести символьный знак равенства (при помощи комбинации [Ctrl+.] или соответствующей пиктограммы панели Evaluation).

Матрицы

Панель операторов с матрицами находится на панели Math.(рис. 4)

Рис.4. Панель операторов с матрицами.

кнопками панели закреплены следующие функции:

– определение размеров матрицы;

– ввод нижнего индекса;

– вычисление обратной матрицы;

– вычисление определителя матрицы: ; вычисление длины вектора ;

 — поэлементные операции с матрицами: если , то ;

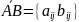– определение столбца матрицы: – j -й столбец матрицы M;

– транспонирование матрицы:

– вычисление скалярного произведения векторов: ;

• — вычисление векторного произведения векторов:

– вычисление суммы компонент вектора: ;

– определение диапазона изменения переменной;

– визуализация цифровой информации, сохраненной в матрице.

Для решения задач линейной алгебры в MathCAD встроены матричные функции. Их можно разделить на две основные группы:

• функции определения (генерации) матриц и операции с блоками матриц;

• функции, реализующие численные алгоритмы решения задач линейной алгебры.

Из каждой группы приведем по несколько, наиболее часто используемых функций.

Первая группа:

1. matrix(m, n, f) – создает и заполняет матрицу размерности , элемент которой, расположенный в i-ой строке и j-ом столбце равен значению функции ;

2. diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;

3. identity(n) – создает единичную матрицу порядка n;

4. augment(A, B) –объединяет матрицы A и B; матрица B располагается справа от матрицы A, при этом матрицы должны иметь одинаковое число строк;

5. stack(A, B) – объединяет матрицы A и B, матрица В располагается внизу под матрицей А, при этом матрицы должны иметь одинаковое число столбцов;

6. submatrix(A, ir, jr, ic, jc) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с ir по jr и в столбцах с ic по jc, причем ir  jr, ic  jc.

На рисунке 5 изображены некоторые из приведенных выше функций в действии.

Вторая группа:

1. rref(A) – приведение матрицы к ступенчатому виду с единичным базисным минором (выполняются элементарные операции со строками матрицы: перестановка строк, умножение строки на число, сложение строк);

2. rank(A) – вычисляет ранг матрицы А (количество линейно-независимых строк или это число ненулевых строк ступенчатой матрицы rref(A));

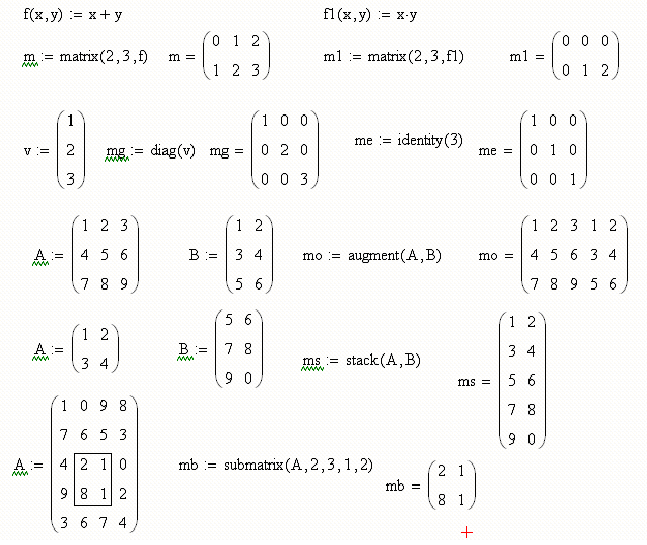
Рис. 5. Операции с матрицами.

3. eigenvals(A) – вычисление собственных значений квадратной матрицы А;

4. eigenvecs (A) – вычисление собственных векторов квадратной матрицы А, значением функции является матрица, столбцы которой есть собственные векторы матрицы А, причем порядок следования векторов отвечает порядку следования собственных значений, вычисленных с помощью функции eigenvals(A);

5. eigenvec(A,e) – вычисление собственного вектора матрицы А, отвечающего собственному значению e;

6. normi(A) – max – норма, или  - норма (infinity norm). в линейной алгебре используются различные матричные нормы, которые ставят в соответствие матрице некоторую скалярную числовую характеристику;

7. lsolve (A,b) – решение системы линейных алгебраических уравнений вида .

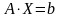Функции второй группы реализуют, как правило, довольно сложные вычислительные алгоритмы. Приведем примеры на использование функций rref и функций для вычисления собственных значений и собственных векторов матрицы.

На рисунке 6 изображены некоторые из приведенных выше функций в действии.

Рис. 6. Операции с матрицами.

В самом простом виде задача на собственные значения матрицы формулируется следующим образом: требуется найти такие значения , чтобы матричное уравнение имело решение. В таком случае число называют собственным числом матрицы А, а n – компонентный вектор Х, приводящий уравнение с заданным в тождество – собственным вектором. В вышеприведенном примере собственные вектора матрицы А получены в матрице MS. Проверка проведена для первого столбца матрицы MS и соответствующего ему собственного числа