19. Идеальные градиентные системы X(y). Схемы расположения.

Для создания градиентного магнитного поля в поперечном направлении X или Y Голлей предложил использовать систему седлообразных катушек. Градиентная система X состоит из четырех симметричных катушек, каждая из которых содержит два дуговых и два линейных участка (рис. 2.5.3). Градиентные системы Х и Y одинаковы по конструкции, но развернуты относительно друг друга вокруг оси Z на 90°.

Рис. 2.5.3. Схема градиентной системы Х

Обозначим расстояние по координате от центра системы координат до дугового проводника через , половину угла раскрыва дуги , радиус дуги и протекающий в ней ток .

Суммарное значение индукции от четырех дуговых участков определяется из выражения

B_z=B_zA+B_zB+B_zC+B_zD. (2.5.8)

Положение дуговых участков и величина центрального угла в такой градиентной системе выбрано из условия равенства нулю члена 3-го порядка в разложении в ряд функции (2.2.2)

. (2.5.9)

Таким образом найдены решения , и . К недостаткам описанной градиентной системы можно отнести ее большую длину, часто превышающую габаритные размеры основной магнитной системы.

20. Аксиальные градиентные системы X(y).

Градиентные системы поперечного градиента

Для создания градиентного магнитного поля в поперечном направлении X или Y Голлей предложил использовать систему седлообразных катушек. Градиентная система X состоит из четырех симметричных катушек, каждая из которых содержит два дуговых и два линейных участка (рис. 2.5.3). Градиентные системы Х и Y одинаковы по конструкции, но развернуты относительно друг друга вокруг оси Z на 90°.

Рис. 2.5.3. Схема градиентной системы

При расчете таких систем воспользуемся формулами (2.2.2–2.2.5) для аксиальной составляющей индукции магнитного поля в произвольной точке пространства от дуговых участков (рис.2.2.1). Обозначим расстояние по координате от центра системы координат до дугового проводника через , половину угла раскрыва дуги , радиус дуги и протекающий в ней ток .

Суммарное значение индукции от четырех дуговых участков определяется из выражения

. (2.5.8)

Положение дуговых участков и величина центрального угла в такой градиентной системе выбрано из условия равенства нулю члена 3-го порядка в разложении в ряд функции (2.2.2)

. (2.5.9)

Таким образом найдены решения , и . К недостаткам описанной градиентной системы можно отнести ее большую длину, часто превышающую габаритные размеры основной магнитной системы.

Поиску более компактных решений для построения градиентных систем посвящена работа автора [9]. Возьмем в качестве источника магнитного поля дугу бесконечно тонкого соленоида. Для этого проинтегрируем по выражения 2.2.11, 2.2.14 и запишем функцию индукции магнитного поля в виде ряда

, (2.5.10)

где – линейная плотность тока в катушке, А/м; – коэффициент ряда -го порядка.

В этом случае выражения для и записанные в относительных единицах ( ), имеют вид

, (2.5.11)

. (2.5.12)

На рис.2.5.4 представлены графики функции и в диапазоне значений от 0 до 3.

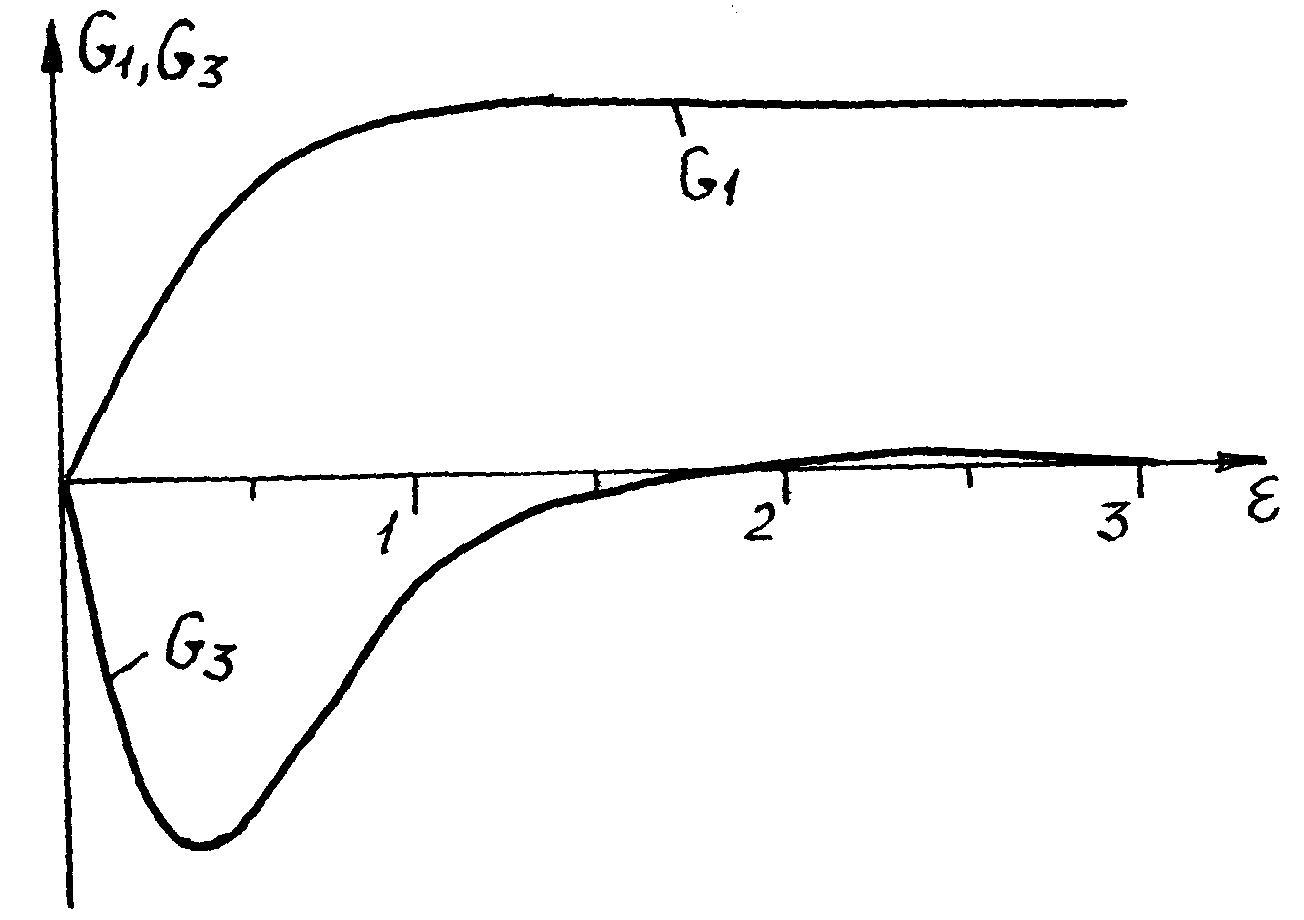
Рис. 2.5.4. Зависимости и от параметра

График имеет экстремумы в точках 0.39 и 2.57, что использовалось некоторыми авторами для компенсации функции (2.5.9). В нашем случае, для заданной ширины катушек , это соответствует единственному решению системы уравнений

(2.5.13)

На рис.2.5.5 пунктирными линиями изображено семейство векторов параметров градиентных систем, полученных при решении системы уравнений (2.5.13). Так как при малых решение имеет известные значения 0.39 и 2.57 назовем такую систему нормальной.

Рис. 2.5.5. Семейства векторов параметров для нормальной

(пунктирная линия) и компактной (сплошная линия) градиентных систем Х

Однако компенсация нежелательного градиента 3-го порядка может быть осуществлена и при других значениях переменных, если перейти к решению системы из трех уравнений

(2.5.14)

Так как система уравнений (2.5.14) избыточна по числу параметров, то для ее решения необходимо задать два независимых параметра, например, ширину катушек и полную длину градиентной системы . Семейство векторов параметров для варианта с и различных значений изображено на рис.2.5.5 сплошными линиями. Назовем такое решение компактным.

Сравнить эффективность двух вариантов градиентных систем можно по значениям функций :

для нормальной ,

для компактной .

На рис.2.5.6 приведена зависимость отношения для различных значений параметра .

Из графика видно, что при эффективность компактной системы несколько больше, чем у нормальной (102%), а при уменьшении габаритного размера до она незначительно падает (до 94%). Дальнейшее уменьшение габаритов градиентной системы нецелесообразно, так как ее эффективность при этом резко падает. Характеристики системы Голея будут приведены ниже.

Для синтеза градиентных систем более высокого порядка локальным методом можно использовать методику, описанную в части 2.5.1 работы, но практика показывает, что при этом градиентные системы имеют большие габариты, и низкую эффективность.

Рис. 2.5.6. Зависимость эффективности компактной градиентной системы от габаритного размера ( )

Для улучшения характеристик системы воспользуемся методом оптимизации. Расчет градиентной системы произведем, используя схему, изображенную на рис.2.5.7 и формулы 2.2.3–2.2.6. Пусть каждая из четырех обмоток состоит из секций, расположенных на расстояниях от центра системы, содержащих дуговых участков с радиусом , центральным углом и соединяющих их прямолинейных участков, параллельных оси .

Участки с обратным направлением тока расположены на расстоянии от центра системы и содержат суммарное число дуговых участков.

Синтезирующее уравнение для такой градиентной системы имеет вид

. (2.5.15)

Таким образом, описываемая градиентная система имеет независимых параметров С. При использовании алгоритма многомерной оптимизации, для найдены значения параметров переменных: , , , , , , и , при которых область с нелинейностью менее 1% максимальна [23]. Сравнение параметров градиентных систем двух типов приведено в табл.2.5.3. Из таблицы следует, что синтезированная система имеет вдвое больший относительный рабочий объем и эффективность по сравнению с системой Голея.

Рис. 2.5.7. Схема расчета градиентной системы

Таблица 2.5.3

Параметр	Система Голея	Оптимизиро-рованная
Габаритный размер	5.14	3.50
Число секций	1	3
Отношение токов в секциях	1:1	1:1:2
Диаметр сферы с нели­нейностью менее 1%	0.40	1.0
Эффективность	100%	270%
Потребляемая мощность	100%	38%

Анализ различных вариантов этого решения показал, что размеры области с высокой линейностью градиента в пределах 50% внутреннего диаметра сохраняются при следующих изменениях параметров: , , , и .

Таким образом, оптимизация параметров позволяет улучшить технические характеристики градиентных систем.