16. Метод знаходження екстремумів функції багатьох змінних: виключення частини змінних Якобі.

Имеется необходимое условие глобального характера, связанное с поведением множества экстремалей, близких к заданной экстремали (см. Якобы условие). Для задачи (3) условие Якоби состоит в следующем. Для того чтобы экстремаль x(t) доставляла минимум в задаче (3), необходимо, чтобы решение уравнения ( Якоби уравнения)

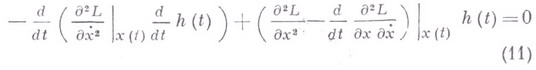
с краевыми условиями не имело бы нулей в интервале . Нули решения уравнения (11) наз. точками, сопряженными с точкой . Таким образом, условие Якоби заключается в том, что интервал не должен содержать точек, сопряженных с .

Необходимые условия слабого минимума , являются точными аналогами условий минимума для функций одного переменного. Условие Якоби при выполнении Лежандра условия (усиленного) является необходимым условием неотрицательности второй вариации. Это приводит к следующему результату: для того чтобы функция x(t).реализовывала слабый минимум функционала (3), необходимо, чтобы: а) функция удовлетворяла уравнению Эйлера, б) выполнялось условие Лежандра в) интервал не содержал точек, сопряженных с точкой t₀ (при условии, что выполняется усиленное условие Лежандра).

17. Метод множителей Лагранжа.

Метод множителей Лагранжа, метод нахождения условного экстремума функции , где , относительно ограничений , где меняется от единицы до .

• Составим функцию Лагранжа в виде линейной комбинации функции и функций 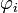, взятых с коэффициентами, называемыми множителями Лагранжа — :

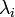где .

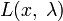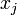• Составим систему из уравнений, приравняв к нулю частные производные функции Лагранжа по и .

• Если полученная система имеет решение относительно параметров 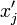и 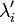, тогда точка 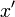может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.

18 . Опуклі множини та їх властивості.

Опукла множина — підмножина евклідового простору яка містить відрізок, який з'єднує будь які дві точки цієї множини.

Іншими словами, множина називається опуклою, якщо:

Тобто, якщо множина разом з будь якими двома точками , які належать цій множині, містить відрізок, який їх з'єднує:

.

У просторі опуклими множинами будуть пряма, напівпряма, відрізок, інтервал, одноточкова множина.

У просторі опуклим буде сам простір, будь який його лінійний підпростір, куля, відрізок, одноточкова множина. Також, опуклими будуть такі множини:

• пряма 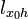, що проходить через точку в напрямку вектора :

;

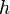• промінь 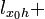, який виходить із точки в напрямку вектора :

;

• гіперплощина H_pβ з нормаллю p:

;

• півпростори на які гіперплощина поділяє простір:

,

.

Всі перелічені множини (крім кулі) є частковими випадками опуклої множини поліедру.

Властивості опуклих множин

• Перетин опуклих множин є опуклим.

• Лінійна комбінація точок опуклої множини опукла.

• Опукла множина містить будь яку опуклу комбінацію своїх точок.

• Будь яку точку n-вимірного евклідового простору з опуклої оболонки множини можна представити як опуклу комбінацію не більш ніж n+1 точок цієї множини.