30. Покоординатний спуск. Введение

Рассмотрим задачу поиска минимума функции , записываемую в виде:

(1)

В этой статье описан метод покоординатного спуска, решающий поставленную задачу. Также приведена теорема сходимости метода покоординатного спуска.

Метод покоординатного спуска Алгоритм

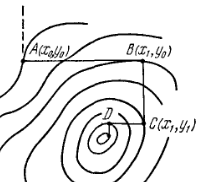
Рис.1 Иллюстрация метода

Вход: функция

Выход: найденная точка оптимума

1. Инициализация некоторым значением

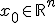
2. повторять:

   • для

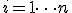
     1. фиксируем значения всех переменных кроме 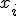, получая одномерную функцию

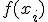
     2. проводим одномерную оптимизацию по переменной , любым методом одномерной оптимизации

     3. если выполен критерий останова (варианты описаны ниже), то возвращаем текущее значение

Критерий останова

Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:

1. 

2. 

Здесь - значение, полученное после -го шага оптимизации. - наперед заданное положительное число.

Сходимость метода

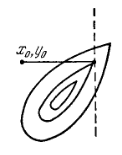
Рис.2

Легко убедится, что существуют функции, когда метод координатного спуска не приводит даже в локальный оптимум.

Пусть линии уровня образуют истинный овраг (рис.2), когда спуск по любой координате приводит на <<дно>> оврага, а любое движение по следующей координате (пунктирная линия) ведет на подъем. Никакой дальнейший спуск по координатам в данном случае невозможен, хотя минимум еще не достигнут.

Теорема о сходимости метода покоординатного спуска.

Для простоты рассмотрим функцию двух переменных . Выберем некоторое начальное приближение и проведем линию уровня через эту точку. Пусть в области , ограниченной этой линией уровня, выполняются неравенства, означающий положительную определенность квадратичной формы:

Тогда спуск по координатам сходится к минимуму из данного начального приближения, причем линейно.

Числовые примеры

Для исследования сходимости метода покоординатного спуска была выбрана функция:

.

Начальное приближение - точка (10,10). Использован критерий останова:

Для решения одномерных задач оптимизации использован метод золотого сечения.

Метод получил точность 1e-8 за 7 итераций.

Отсюда можно сделать вывод, что метод координатного спуска сходится неплохо на примерах, для которых он применим.

31,32. Градієнтні методи.

2. Градієнтні методи

Основна ідея методів полягає в тому, щоб йти в напрямку найшвидшого спуску, а цей напрямок задається антіградіента :

де λ ^[j] вибирається

• постійною, в цьому випадку метод може розходитися;

• дробовим кроком, тобто довжина кроку в процесі спуску ділиться на деяке число;

• порад задля спуском:

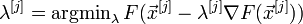
2.1. Метод найшвидшого спуску (метод градієнта)

Вибирають , Де всі похідні обчислюються при , І зменшують довжину кроку λ ^[j] у міру наближення до мінімуму функції F .

Для аналітичних функцій F і малих значень f _i Тейлоровской розкладання F (λ ^[j]) дозволяє вибрати оптимальну величину кроку

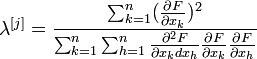(5)

де всі похідні обчислюються при . Параболічна інтерполяція функції F (λ ^[j]) може виявитися більш зручною.

2.1.1. Алгоритм

1. Задаються початкове наближення і точність розрахунку

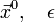
2. Розраховують , Де

3. Перевіряють умова зупину:

   • Якщо 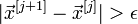, То j = j + 1 і перехід до кроку 2.

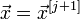   • Інакше і зупинка.

2.2. Метод покоординатного спуску ( Гаусса-Зейделя)

Покращує попередній метод за рахунок того, що на черговій ітерації спуск здійснюється поступово уздовж кожної з координат, однак тепер необхідно обчислювати нові раз за один крок.

2.2.1. Алгоритм

1. Задаються початкове наближення і точність розрахунку

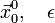
2. Розраховують 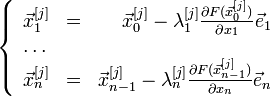, Де

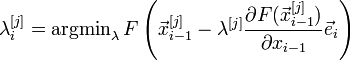
3. Перевіряють умова зупину:

   • Якщ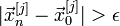о , То 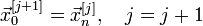і перехід до кроку 2.

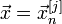   • Інакше і зупинка.

2.3. Метод спряжених градієнтів

Метод спряжених градієнтів грунтується на поняттях прямого методу багатовимірної оптимізації - методу сполучених напрямків.

Застосування методу до квадратичним функцій в визначає мінімум за n кроків.

2.3.1. Алгоритм

1. Задаються початковим наближенням і похибкою:

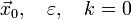
2. Розраховують початкова напрям:

3. 

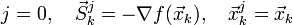
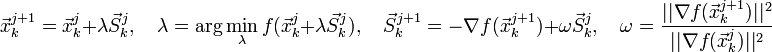
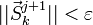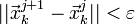   • Якщо або , То 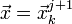і зупинка.

   • Інакше

     • якщо (J + 1) <n< i=""> </n<> , То j = j + 1 і перехід до 3;

     • інакше 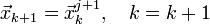і перехід до 2.