7. Анализ чувствительности скорректированной системы.

Для анализа чувствительности скорректированной системы выберем в качестве нестабильного звена усилитель. Исследуем разброс значений показателей качества при изменении коэффициента усиления k_У в пределах 120-180. Показатель колебательности M должен быть меньше 1.2, а время регулирования t_Р минимально из всего набора полученных значений. Для наглядности результаты представлены в таблице 1.

kУ	tР,с	M
120	0.12	1.048
130	0.10	1.045
140	0.09	1.042
150	0.08	1.040
160	0.07	1.038
170	0.07	1.036
180	0.11	1.035

Табл.1. Анализ чувствительности скорректированной системы.

Полученные значения показывают, что показатель колебательности удовлетворяет условию задания (меньше 1.2), а минимальное время регулирования равно 0.07 с. Можно сделать вывод, что скорректированная система достаточно устойчива и удовлетворяет заданным показателям качества в пределах погрешности (лучшие показатели достигаются при k_У =170,что можно практически реализовать).

8. Анализ нелинейной системы.

8.1. Моделирование системы в simulink.

С помощью инструмента Simulink из пакета MATLAB введем модель системы в ЭВМ. Получим следующую схему:

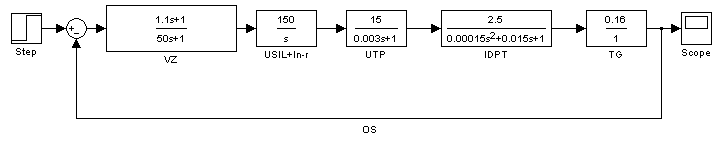
Рис. 13. Схема скорректированной системы, полученная путем моделирования в Simulink.

После моделирования процесса в Simulink видно, что результаты (см. рис. 14) совпадают с результатами, полученными при помощи программы CLASSIC (см. рис. 11).

h(t)

t, с

Рис.14. График переходного процесса скорректированной системы, полученный путем моделирования в Simulink.

8.2. Ввод нелинейного элемента.

В реальных системах обычно присутствуют нелинейные элементы. Это могут быть звенья релейного типа, звенья с кусочно-линейной характеристикой, звенья с криволинейной характеристикой, нелинейные импульсные звенья, логические звенья и др. Рассмотрим нелинейность типа насыщение. Блок Saturation (Насыщение) представляет собой одну из распространенных нелинейностей в цепях с усилителями, которые обычно имеют ограничения в усилении входного сигнала уровнем питающего его напряжения.

Рассмотрим данный элемент подробнее:

Назначение: выполняет ограничение величины сигнала. Параметры:

1. Upper limit-верхний порог ограничения.

2. Lower limit-нижний порог ограничения.

3. Treat as gain when linearizing (флажок)-трактовать как усилитель с коэффициентом передачи равным 1 при линеаризации.

Выходной сигнал блока равен входному если его величина не выходит за порог ограничения. По достижении входным сигналом уровня ограничения выходной сигнал блока перестает изменяться и остается равным порогу. На рис. 15 показан пример использования блока для ограничения синусоидального сигнала. На рисунке приводятся временные диаграммы сигналов и зависимость выходного сигнала блока от входного.

Рис.15. Пример использования блока Saturation.

На рис. 16 представлена схема скорректированной системы с введенным нелинейным элементом.

Рис. 16. Схема нелинейной системы с блоком Saturation.

На рис.17 изображено действие блока насыщение. Входной сигнал (1) подается с выхода УТП, результат на выходе блока (2) подается на вход ИД. Заданы условия границы насыщения сверху 2.57 В, снизу 0 В, из рисунка можно получить полное представление о нелинейности типа насыщение на входной сигнал.

U, В

t, с

Рис. 17. Сигналы на входе блока Saturation (1) и на его выходе (2).

Исходный максимальный уровень напряжения на двигателе (без ограничения насыщение) равен 2.76 В.

На рис.18 приведен пример изменения графика переходного процесса при введении нелинейности насыщения с параметрами насыщения 2.55 В – 0 В. Видно как при ограничении максимального напряжения, подаваемого на исполнительный двигатель, время затухания сигнала увеличивается, график исходного переходного процесса (1) при насыщении имеет вид (2).

t, с

h(t)

Рис. 18. Изменение характера переходного процесса при введении блока Saturation.

Далее будут проанализированы параметры переходного процесса при введении насыщения и сделаны выводы об изменениях в системе при добавлении нелинейного звена. В таблице 2 представлены изменения параметров переходного процесса, характеризующих систему.

Границы насыщения, В	Значение перерегулирования σ, %	Время регулирования tр, с
2.6..- 0	4.0192	0.0873
2.57..- 0	2.8759	0.0873
2.55..- 0	2.0751	0.0873
2.5..- 0	0.8889	0.0873
2.45..- 0	0	0.0932
2.4..- 0	0	0.0844
2.35..- 0	0	0.092
2.3..- 0	0	∞

Табл.2. Влияние насыщения на характеристики переходного процесса.

Из приведенной таблицы видно, что система достаточно устойчива при границах насыщения 2.6.. - 0. При границах 2.4..- 0 время регулирования оказывается меньше исходного. При границах 2.3..- 0 процесс не входит в полосу 0,95 – 1,05, поэтому его время регулирования равно бесконечности(процесс не сходится к единице).