
2. Анализ объекта
2.1. Линеаризация дифференциальных уравнений объекта
При малых отклонений переменных от точек равновесия гладкие НЭ могут быть заменены линейными звеньями, коэффициенты которых равны tgуглов наклона касательных. ВMatlab\Simulink(в дальнейшем просто вMatlab) есть специальная команда линеаризации:
>>[A,B,C,D]=linmod('имя')
где A,B,C,D– матрицы линеаризованной системы дифференциальных уравнений (ДУ) в форме пространства состояний (ФПС)
ДУ в ФПС выглядят следующим образом:

![]() -
вектор переменных состояния
-
вектор переменных состояния
f– внешнее воздействие на объект
y– выход объекта
Командой linmodполучим матрицы линеаризованной системы:
A =
0 0 0 1.0000
-9.8000 0 0 0
0 1.0000 0 0
0 0 -107.8000 0
B =
0
1
0
0
C =1 0 0 0
D =0
Линеаризованная модель в ФПС в соответствии с полученными матрицами запишется так:
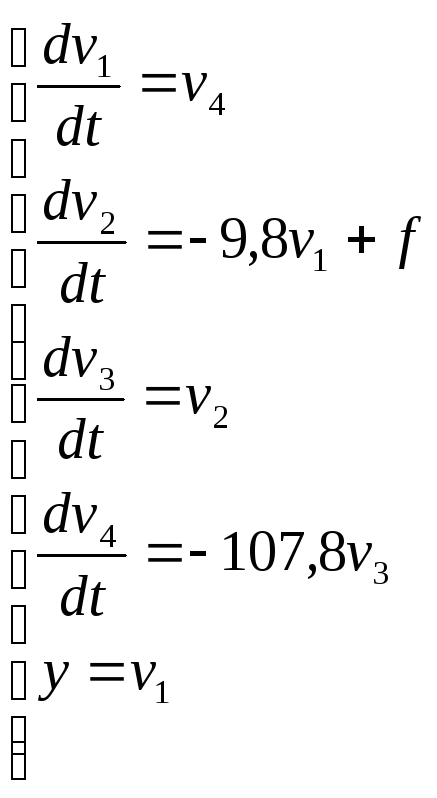
На основе данной системы уравнений делаем вывод какая переменная состояния соответствует какой переменной нашей системы:
![]()
2.2. Анализ устойчивости
Анализ устойчивости сводится к вычислению собственных значений матрицы А. Это можно сделать командой Matlab:
>>eig(A)
ans =
-5.7011
0.0000 + 5.7011i
0.0000 - 5.7011i
5.7011
Анализ устойчивости положения равновесия.
Согласно 1 методу Ляпунова об устойчивости положения равновесия нелинейной системы можно судить по линеаризованным уравнениям вычислением собственных значений матрицы А. Мы получили правый корень. Его наличие означает, что положение равновесие не устойчиво.
Определим передаточную функцию нашей системы. Это можно сделать командой
>>[num,den]=ss2tf(A,B,C,D)
где numиden– соответственно числитель и знаменатель передаточной функции.
num =
-107.8000
den =
1 0 0 0 -105.644
командой
>>printsys(num,den)
можно получить передаточную функцию в привычном виде:
num/den =
-107.8
-------------
s^4 - 1056.44
Полюсы передаточной функции вычисляются командой
>>roots(den)
ans =
-5.7011
-0.0000 + 5.7011i
-0.0000 - 5.7011i
5.7011
Они, естественно, совпадают с собственными значениями матрицы А.
2.3. Анализ управляемости и наблюдаемости объекта.
Синтез управляющего устройства начинается с анализа таких свойств объекта как управляемость и наблюдаемость. В соответствие с критерием Калмана объект управляем полностью, если матрица управляемости имеет полный ранг. В нашем примере она должна иметь ранг равный 4.
Вычислим матрицу управляемости.
>>U=ctrb(A,B)
U =
0 0 0 -107.8
1 0 0 0
0 1 0 0
0 0 -107.8 0
Ранг вычисляется командой
rank(U)
ans= 4
Ранг полный, следовательно, объект полностью управляем.
Объект полностью наблюдаем если матрица наблюдаемости имеет полный ранг.
Вычислим матрицу наблюдаемости.
>>V=obsv(A,C)
V =
1 0 0 0
0 0 0 1
0 0 -107.8 0
0 -107.8 0 0
rank(V)
ans = 4
Объект также полностью наблюдаем. Следовательно имеет место синтез управляющего устройства.
