
Лабораторная работа №3
.pdfСанкт-Петербургский Государственный Электротехнический Университет
(ЛЭТИ)
Отчет по лабораторной работе №3
ИССЛЕДОВАНИЕ УСТАНОВИВШИХСЯ ПРОЦЕССОВ В СУ
Выполнили студенты группы 1341, ФКТИ |
Куцелев Н. |
|
Пухкал И. |
|
Трофимов Д. |
Санкт-Петербург 2004

Содержание |
2 |
Содержание
1 |
Постановка задачи |
3 |
2 |
Выполнение работы |
3 |
3 |
Вывод |
15 |

2 Выполнение работы |
3 |
1. Постановка задачи
Цель работы:
Исследование установившихся ошибок в СУ
1. Ввести систему управления со следующими характеристиками WR(s) =
kR, Wp(s) = 1 3 . Постоянная времени T выбирается самостоятельно
(1+T s)
вдиапазоне 0.1 ÷ 10 сек.
(a)Установить kR = 1. Определить переходную характеристику и по ней определить установившуюся ошибку εó . Рассчитать теоретическое значение и сравнить с экспериментальным.
(b)Рассчитать критическое значение kRk и повторить пункт 1a, установив kR = kRk · 0.8.
(c)При kR = kRk · 0.8 подать на вход системы линейно нарастающий входной сигнал xó = kt. Для формирования сигнала использовать формирующий фильтр. Значение k выбрать самостоятельно, с учетом ранее выбранной T. Оценить результаты.
2.Изменить ПФ регулятора, введя интегральный закон регулирования: WR =
ksR .
(a)Рассчитать критическое значение kRk и установить kR = kRk · 0.7.
(b)Повторить исследование ошибки при xó = f(t) и xó = kt.
(c)Подать на систему параболический входной сигнал xó = kt2 и исследовать ошибку.
3. Ввести систему с ПФ: Wp(s) = |
1 |
, WR = |
kR(1+TRs) |
(T1 = 10 с, |
(1+T1s)(T2s+1) |
s |
T2 = 0.01 с, kR = 100 с−1, TR = 1 с).
(a)Определить диапазон частот входного синусоидального сигнала xó = a sin ωkt, амплитуды которых ослабляются на выходе не менее, чем в 100 раз. Определить диапазон частот, которые практически не отрабатываются системой. Подтвердить результаты теоретически.
(b)Подать на вход экспоненциальное воздействие: xó = e−kt. Определить ошибку.
4.Сформулировать основные выводы по работе, привести теоретические подтверждения.
2.Выполнение работы
Здесь и далее будем полагать T = 1 с
1.Wp = (s+1)1 , WR = kR
(a)kR = 1.
2 Выполнение работы |
4 |
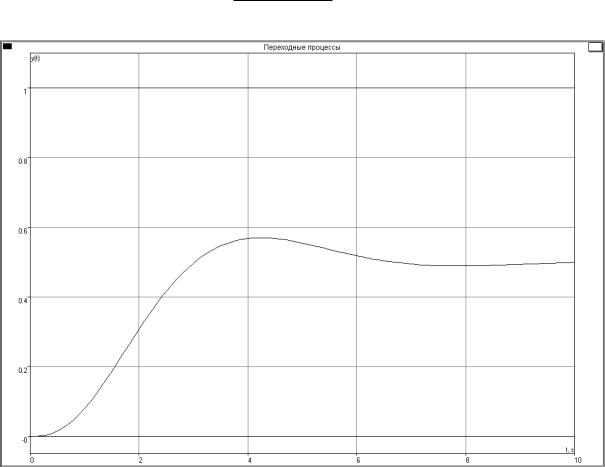
Переходная характеристика замкнутой системы
Φ(s) = |
WR(s)Wp(s) |
|||||
1 + WR(s)Wp(s)WÎÑ (s) |
|
|
||||
|
|
1 |
1 |
|
|
|
Wp(s) = |
|
= |
|
|
||
(s + 1)3 |
s3 + 3s2 + 3s + 1 |
|||||
|
|
|
1 |
|
|
|
Φ(s) = s3 + 3s2 + 3s + 2
Рис. 1. Результат анализа программой «Классик»: Переходные процессы
Установившаяся ошибка
εó = lim ε(t) = lim sε(s) = lim sΦ0(s)xó (s)
t→∞ s→0 s→0
|
|
|
|
s3 |
+ 3s2 + 3s + 1 |
1 |
1 |
||||
εó = lim s |
|
|
|
|
|
|
= |
|
|
||
· |
s3 |
+ 3s2 + 3s + 2 |
· s |
|
|||||||
s |
→ |
0 |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

2 Выполнение работы |
5 |
Рис. 2. Результат анализа программой «Классик»: График ошибки
Ном.Система Установившееся значение: 0.5000
(b)kR = kRk · 0.8
Критическое значение kRk
1
Φ(s) = s3 + 3s2 + 3s + 1 + kêð
3 |
1 + kêð |
0 |
|
= 1 |
3 |
0 |
03 1 + kêð
1 = 3 > 0
2 |
= |
3 |
1 + kêð |
|
= 9 − (1 + kêð) = 8 − kêð = 0 |
1 |
3 |
||||
|
|
|
|
|
|
|
|
|
|
|
|

2 Выполнение работы |
6 |
3 1 + kêð |
0 |
3 = 1 |
3 |
0 = 9 − (1 + kêð) = 8 − kêð = 0 |
0 |
3 |
1 + kêð |
kêð = 8
Рис. 3. Результат анализа программой «Классик»: Комплексная плоскость
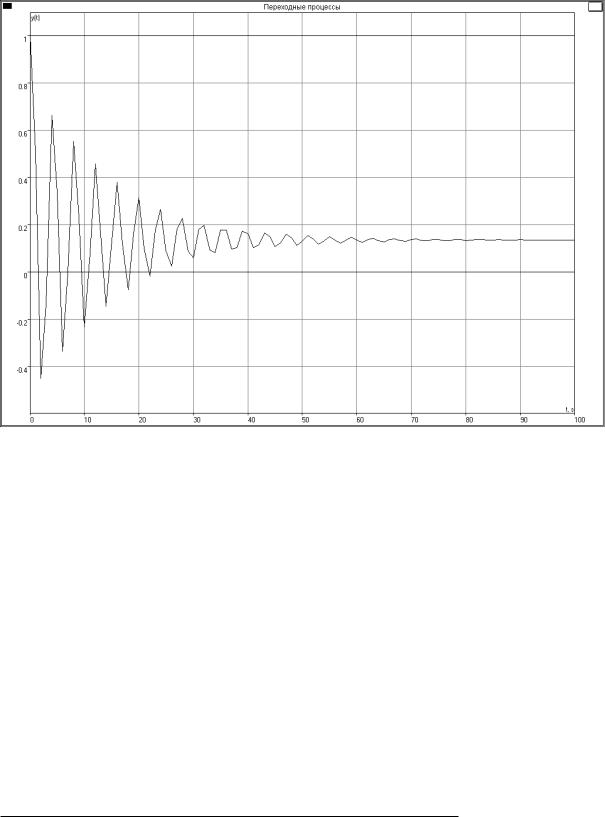
Переходная характеристика замкнутой системы
WR(s)Wp(s)
Φ(s) = 1 + WR(s)Wp(s)WÎÑ (s)
6.4
Φ(s) = s3 + 3s2 + 3s + 7.4

2 Выполнение работы |
7 |
Рис. 4. Результат анализа программой «Классик»: Переходные процессы
Установившаяся ошибка |
|
|
|
||||||||
|
|
|
|
|
|
s3 + 3s2 + 3s + 1 1 |
1 |
|
|||
εó |
lim s |
|
|
|
|
|
= |
|
= 0.1351 |
||
· |
s3 + 3s2 + 3s + 7.4 · s |
|
|||||||||
|
= s |
→ |
0 |
7.4 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 Выполнение работы |
8 |
Рис. 5. Результат анализа программой «Классик»: График ошибки
Ном.Система Установившееся значение: 0.1351
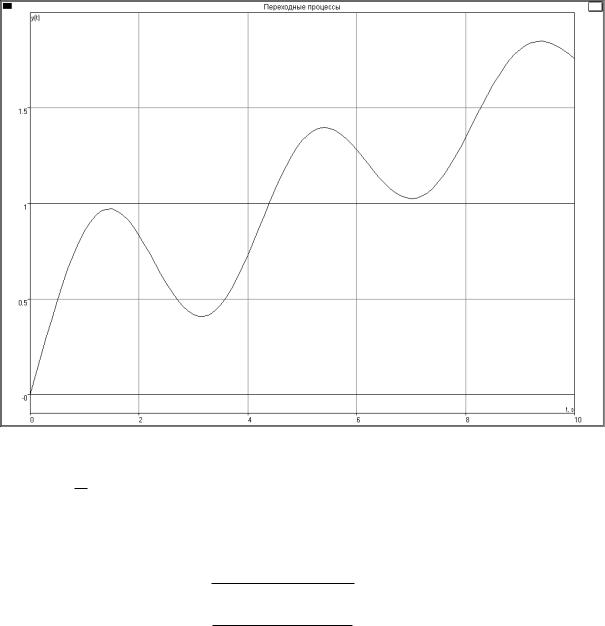
(c)xó = t
Установившаяся ошибка
εó |
lim s |
|
s3 + 3s2 + 3s + 1 1 |
= ∞ |
|||||
|
|
|
|
||||||
· s3 + 3s2 + 3s + 7.4 · s2 |
|||||||||
|
= s |
→ |
0 |
||||||
|
|
|
|
|
|
|
|
||
Ном.Система Процесс расходящийся
2 Выполнение работы |
9 |
Рис. 6. Результат анализа программой «Классик»: График ошибки
2.WR = ksR
(a)kR = 0.7 · kRk
Критическое значение kRk
WR(s)Wp(s)
Φ(s) = 1 + WR(s)Wp(s)WÎÑ (s)
Φ(s) =
kêð
s4 + 3s3 + 3s2 + s + kêð
|
3 |
1 |
|
0 |
0 |
|
|
1 |
3 |
kêð |
0 |
||
1 |
3 |
|
0 |
kêð |
||
= |
|
|
|
|
|
|
|
0 |
3 |
|
1 |
0 |
|
|
1 = |
3 |
> 0 |
|
|
|
|
|
|
|
|
|
|
2 |
= |
3 |
1 |
= 9 − 1 = 8 > 0 |
1 |
3 |
|||
|
|
|
|
|
|
|
|
|
|
2 Выполнение работы |
10 |
3 1 0
1 |
3 |
kêð |
|
= 9 − |
êð |
− 9k |
êð |
= 0 |
||
3 = 0 |
3 |
1 |
(1 + 9k ) = 8 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 = kêð 3 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
kêð = |
8 |
= 0.889 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
9 |
|
|
|
|||||
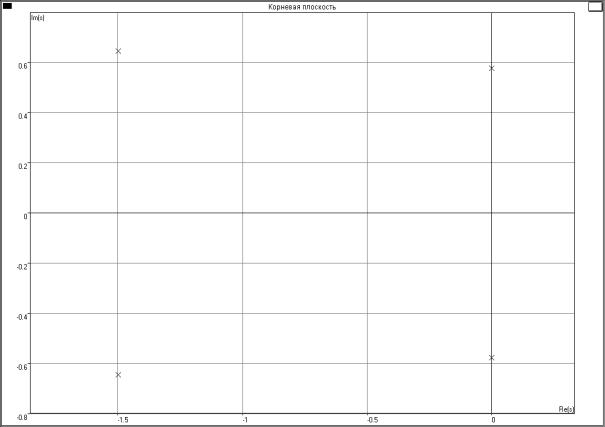
Рис. 7. Результат анализа программой «Классик»: Комплексная плоскость
•x(t) = 1(t)
Установившаяся ошибка
εó |
lim s |
· |
s4 + 3s3 + 3s2 + s |
|
· |
1 |
= 0 |
||||
|
|
|
|
|
|||||||
s4 + 3s3 + 3s2 + s + 0.889 |
|
s |
|||||||||
|
= s |
→ |
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
