8.2. Парная регрессия

Определение параметров уравнения корреляции (регрессии) осуществляется с помощью метода наименьших квадратов. Для расчета параметров линейного уравнения необходимо решить систему нормальных уравнений:

(8.5)

где п - число единиц наблюдения.

В уравнении регрессии показывает усредненное влияние неучтенных (не выделенных для исследования) факторов на результативный признак; параметр показывает, насколько в среднем изменяется значение результативного признака при изменении факторного на единицу его собственного измерения.

Если связь между признаками х и у криволинейная и описывается уравнением параболы второго порядка, то система нормальных уравнений имеет вид:

(8.6)

Оценка обратной зависимости межу х и у, когда с увеличением (уменьшением) х уменьшается (увеличивается) значение результативного признака у, может быть осуществлена на основе уравнения гиперболы.

Система нормальных уравнений для нахождения гиперболы следующая:

(8.7)

Оценка тесноты связи между исследуемыми признаками проводится при помощи коэффициента корреляции (r). Расчет данного коэффициента проводится по формуле

, (8.8)

где , , , (8.9)

- среднее квадратическое отклонение х и у.

(8.10)

Линейный коэффициент корреляции изменяется в пределах от -1 до 1. Интерпретация значений коэффициента корреляции представлена в табл. 8.2.

Таблица 8.2

Оценка линейного коэффициента корреляции

Значение коэффициента корреляции	Характер связи	Интерпретация связи
r = 0	отсутствует	показатели между собой не связаны
0< r <1	прямая	с увеличением х увеличивается у
-1< r <0	обратная	с увеличением х уменьшается у, и наоборот
r = ±1	функциональная	каждому значению факторного признака строго соответствует одно значение результативного признака

8.3. Многофакторная регрессия

Наибольший успех в изучении связей между социально-экономическими величинами достигается тогда, когда используются методы множественной (многофакторной) регрессии. При исследовании таких связей необходимо найти аналитическое выражение зависимости результативного признака (у) от трех и более факторных признаков (х₁, х₂, … , х_n).

Практика построения многофакторных моделей показывает, что все реально существующие взаимосвязи между социально-экономическими явлениями можно описать, используя линейную, параболическую, гиперболическую, степенную или показательную функцию. Наибольшее распространение в силу простоты и логичности экономической интерпретации имеют линейные модели. Нелинейные формы зависимости можно привести к линейным путем линеаризации.

Простейшим примером множественной регрессии является связь между тремя факторами, которая может быть выражена уравнением

. (8.11)

Решение системы нормальных уравнений позволяет определить параметры а₀, а₁, а₂:

,

, (8.12)

.

Оценить тесноту связи между результативным (у) и двумя факторными признаками (х₁ и х₂) можно, рассчитав множественный коэффициент регрессии R:

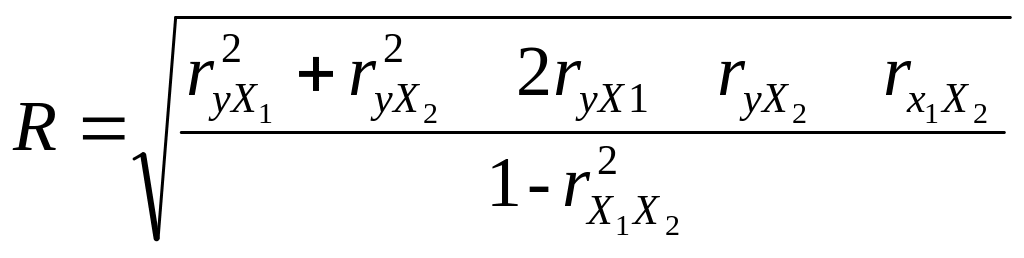, (8.13)

где r – парные коэффициенты корреляции меду признаками.

Для оценки степени влияния фактора (факторов) на результативный признак используется коэффициент детерминации (D). Этот показатель рассчитывается по формуле

D= . (8.14)

Коэффициент детерминации показывает, на сколько процентов изменение результативного признака объясняется изменением факторного (всех факторных) признака.

Для экономической интерпретации используется коэффициент эластичности (Э), который рассчитывается по формуле

. (8.15)

Коэффициент эластичности показывает относительное (%) изменение результативного признака при изменении факторного признака на один процент.

Уравнения как парной, так и множественной зависимости могут быть использованы для целей планирования и прогнозирования.