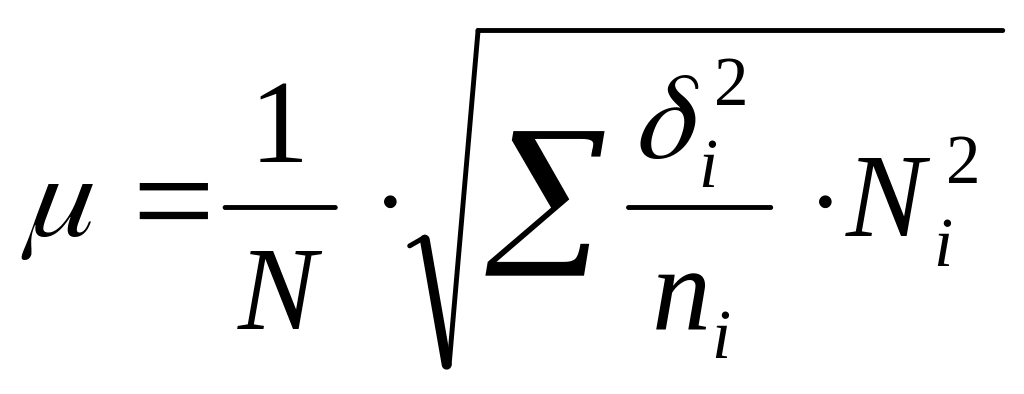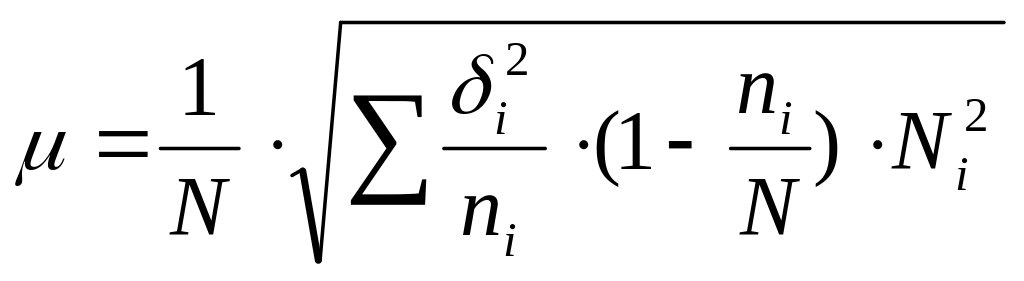7.2. Способы и виды выборки

В статистике применяют различные методы формирования выборочных совокупностей, что обусловлено задачами исследования и спецификой объекта исследования.

Использование научно обоснованных методов формирования выборочной совокупности позволяет избежать систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности.

В зависимости от способа отбора единиц из генеральной совокупности различают повторный и бесповторный отбор. Повторным называют такой отбор, при котором отобранная однажды единица возвращается обратно в генеральную совокупность и снова участвует в выборке. При повторном отборе сохраняется постоянная вероятность попасть в выборку для всех единиц совокупности.

Бесповторным называется такой отбор, при котором отобранная один раз единица обратно в генеральную совокупность не возвращается.

При бесповторном отборе вероятность попадания в выборку у оставшихся единиц увеличивается.

Повторный отбор часто бывает затруднен в организационном плане при проведении экономических исследований, когда генеральная совокупность не существует реально, а мыслится как гипотетически возможная. Именно такая ситуация возникает при обследовании предприятий по их отчетности. Бесповторный отбор дает более точные результаты, чем повторный, т. к. каждая единица совокупности может попасть в выборочную совокупность только один раз, в то время как при повторном отборе одна и та же единица может попасть в выборку несколько раз. В практике статистических исследований используют несколько видов выборки: собственно случайная (простая случайная выборка), механическая, типическая, серийная.

Собственно случайная (просто случайная) выборка состоит в том, что выборочная совокупность образуется в результате случайного (непредвиденного) отбора отдельных единиц из генеральной совокупности. Отбор единиц в выборочную совокупность может быть осуществлен путем жеребьевки или с использованием таблицы случайных чисел (такие таблицы публикуются в приложениях учебников по математической статистике). Для проведения случайной выборки все единицы генеральной совокупности должны быть пронумерованы.

Случайная выборка может быть проведена повторным и бесповторным отбором. Чаще на практике используется бесповторный отбор, что обусловлено требованием повышения степени репрезентативности выборки, особенно при недостаточно больших объемах выборки.

Повторный отбор бывает не всегда целесообразным или просто невозможен. Например, если при контроле качества электроламп они в выборке были подвергнуты проверке на продолжительность горения, то возвращать перегоревшие лампочки в генеральную совокупность не имеет смысла. Но при маркетинговых исследованиях выборочное наблюдение может проводиться по способу повторного отбора. В частности, при изучении мнения населения о качестве организации автобусного движения в городе не исключена возможность повторной регистрации одного и того же респондента.

Для вычисления средней ошибки выборки и необходимой численности случайной выборки используют следующие формулы (табл.7.1):

Таблица 7.1

Расчет выборки численности и средней ошибки выборки

Способы отбора	Показатели
	средняя ошибка выборки	численность выборки
Случайный повторный
Случайный бесповторный

где - дисперсия;

N - численность генеральной совокупности;

- среднее квадратическое отклонение.

Формула для расчета и приведена в главе 4 данного учебного пособия.

Механическая выборка. При такой выборке, по существу, генеральная совокупность разбивается на равные по численности группы и из каждой группы для обследования выбирается одна единица.

Для обеспечения репрезентативности выборки все единицы генеральной совокупности должны быть расположены в определенном порядке по признаку, который определяет поведение изучаемого показателя. В этом случае в выборочную совокупность попадает та единица, которая находится в середине группы.

На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, из списочного состава работников автотранспортного предприятия, представленных в алфавитном порядке, отбирается определенное количество работников.

При проведении механической выборки нужно учитывать точку и шаг отсчета. Точка отсчета - это номер той единицы, которая должна быть обследована первой. Шаг отсчета устанавливают в зависимости от предполагаемого процента отбора. Если из генеральной совокупности объемом 1000 единиц обследованию подлежат 100 единиц, это означает, что из каждых 10 единиц обследованию будет подлежать одна единица, т.е. шаг отсчета равен 10. Механическая выборка по точности результатов близко подходит к собственно случайной выборке. Поэтому расчеты средней ошибки и численности выборки следует производить по формулам случайной бесповторной выборки.

Типическая выборка. При типической выборке генеральная совокупность разбивается на однородные типические группы. Затем из каждой группы механической выборкой, реже собственно случайной, проводится индивидуальный отбор в выборочную совокупность. Типическая выборка обычно используется при изучении сложных статистических совокупностей, например, при выборочном обследовании производительности труда рабочих, состоящих из разных групп по квалификации.

Типические группы, отобранные для исследования, могут быть по объему неравны между собой. В этом случае производится отбор, либо пропорциональный объему групп, либо непропоциональный. В соответствии с этим различают пропорциональную и непропорциональную типическую выборку. Наиболее правильно производить пропорциональный отбор, т.к. он позволяет учесть число единиц, которое имеется в каждой типической группе.

Численность единиц выборки i-ой типической группы (n ) определяется по формуле

. (7.3)

Средние ошибки типической выборки рассчитываются по следующим

формулам (табл.7.2).

Таблица 7.2

Средние ошибки выборки

Способ отбора	Пропорциональная типическая выборка	Непропорциональная типическая выборка
Повторный
Бесповторный

где - средняя из внутригруппировочных дисперсий;

- дисперсия i-той типической группы;

ni - объем выборки i -той типической группы;

n - общий объем выборки;.

Ni - объем i - той типической группы;

N - объем всей генеральной совокупности.

Серийная выборка. При серийной выборке в случайном порядке отбираются группы (серии, гнезда единиц), а не отдельные единицы из генеральной совокупности. Внутри каждой серии, попавшей в выборку, обследуются все без исключения единицы, т. е. применяется сплошное наблюдение.

Группы (серии) отбираются по случайной бесповторной выборке или с помощью механического отбора. В серийной выборке каждая серия играет такую же роль, как отдельная единица при индивидуальном отборе. Серийная выборка используется при контроле качества товара, поступающего в упаковке (пачки, коробки, ящики), где находится не одна единица товара, а какое - то его количество. В этом случае целесообразнее проверить несколько отдельных упаковок (серий), чем из всех упаковок отобрать необходимое количество единиц товара.