5. Ряды динамики и их анализ
5.1. Виды рядов динамики, методы расчета показателей ряда динамики
Процессы, происходящие на транспорте, претерпевают постоянные изменения во времени. Эти изменения можно изучать, если иметь данные по определенному кругу показателей за ряд промежутков времени или на ряд моментов времени, следующих друг за другом. Последовательность значений статистического показателя, расположенных в хронологическом порядке, называется рядом динамики.
Ряды динамики используются для изучения изменений во времени, их анализа, выявления тенденций, установления закономерностей и прогнозирования показателей. Каждый ряд динамики состоит из двух элементов: первый – показатель времени, к которому относятся регистрируемые события, второй представляет числовую характеристику изучаемого явления и называется уровнем ряда динамики.
Уровни ряда могут быть выражены абсолютными, относительными или средними величинами. В рядах динамики выделяют начальный (первый) и конечный (последний) уровень ряда.
В качестве показателей времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяца, сутки).
Ряды динамики, в зависимости от отражаемого в них времени, делятся на интервальные и моментные.
Моментный ряд динамики показывает состояние какого-либо явления на определенные моменты времени. Например, число единиц подвижного состава на начало каждого квартала в течение года.
Интервальный ряд динамики представляет статистические данные, характеризующие размеры явления за определенные промежутки времени. Примером интервального ряда динамики может служить объем перевозок предприятия по месяцам в течение года.
Важным условием правильного формирования рядов динамики является сопоставимость уровней, образующих ряд. Основным требованием сопоставимости уровней является одинаковая методология их исчисления для всех периодов или дат. При этом все уровни должны быть даны не только в одних и тех же, но и равноценных единицах измерения. Условием сопоставимости данных является также одинаковая полнота охвата различных частей явления, представленного рядом динамики и равенством периодов, за которые приводятся данные. Нельзя в один ряд динамики включать данные о работе предприятия за месяц и квартал, т.к. такие данные несопоставимы.
В зависимости от расстояния между уровнями ряды динамики могут быть с равноотстоящими уровнями и неравноотстоящими уровнями во времени. Ряды динамики, состоящие из следующих друг за другом периодов или следующих через определенные промежутки дат, называются равноотстоящими. Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются неравноотстоящими.
Н
аглядное
представление процесса изменения
явления во времени дает графическое
изображение. Наиболее часто для
графической иллюстрации используют
диаграммы и линейные графики.
Для анализа динамики показателей деятельности предприятия используют следующие показатели: абсолютный прирост, темп роста, темпы прироста, абсолютное значение одного процента прироста, темп наращивания.
В основе расчета показателей ряда динамики лежит сравнение его уровней. В зависимости от способа сравнения показатели могут быть цепными (с переменной базой сравнения) и базисными (с постоянной базой сравнения). Схематическое построение цепных и базисных показателей представлено на рис. 5.1.
базисные
показатели
...
...
цепные
показатели
Рис.5.1. Схема построения показателей ряда динамики в зависимости от базы сравнения
где Х1 - начальный уровень ряда;
Хn - конечный уровень ряда;
Xi - уровень ряда.
При расчете цепных показателей каждый последующий уровень ряда сравнивается с предыдущим. Расчет базисных показателей определяется сравнением каждого уровня с одним, как правило, начальным уровнем, принятым за базу сравнения.
Формулы для расчета основных показателей ряда динамики приведены в табл. 5.1
Таблица 5.1
Расчет показателей ряда динамики
Показатель |
Цепной
|
Базисный |
Абсолютный прирост, А |
|
|
Темп роста, Tp |
|
|
Темп прироста, Tпр |
|
|
Абсолютный прирост может быть положительным и отрицательным числом и показывает, на сколько уровень изучаемого периода больше или меньше уровня принятого за базу сравнения. Сумма всех цепных абсолютных приростов равна последнему базисному абсолютному приросту. Эту связь можно выразить формулой
.
(5.1)
Между темпами роста и прироста существует взаимосвязь:
.
(5.2)
Темпы роста и прироста обычно выражаются в процентах или в виде простых отношений. Темпы роста, выраженные простыми отношениями, называют коэффициентами роста.
В статистической
практике часто используют абсолютное
значение одного процента прироста (
).
Экономический смысл имеет только цепной
показатель. Расчет ведется по формуле
.
(5.3)
Преобразуя данную форму, можно получить
.
(5.4)
Абсолютное значение одного процента прироста измеряется в тех же единицах измерения, что и исследуемый показатель. Экономическая интерпретация показателя: на сколько изменится величина показателя при изменении его на один процент. Например, абсолютное значение одного процента прироста заработной платы в мае составляет 50 руб. Это означает, что увеличение заработной платы на один процент в мае по сравнению с апрелем составляет 50 руб.
Кроме указанных
показателей, для характеристики динамики
социально-экономических процессов
можно определить темпы наращивания
(
).
Расчет ведется по формулам:
;
(5.5)
.
(5.6)
Для характеристики интенсивности развития за анализируемый период рассчитываются средние показатели динамики. К их числу относятся: средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста, средняя величина одного процента прироста.
Средний уровень ряда динамики определяется различно в зависимости от вида ряда динамики. Для интервального ряда с равноотстоящими уровнями он рассчитывается по формуле простой средней арифметической
.
(5.7)
Для моментного ряда с неравноотстоящими расчет ведется по формуле средней арифметической взвешенной
,
(5.8)
где - уровень ряда динамики;
- длительность интервала времени между уровнями ряда, в течение которого оставался без изменения.
Если моментный ряд имеет равноотстоящие уровни, то расчет ведется по формуле средней хронологической
.
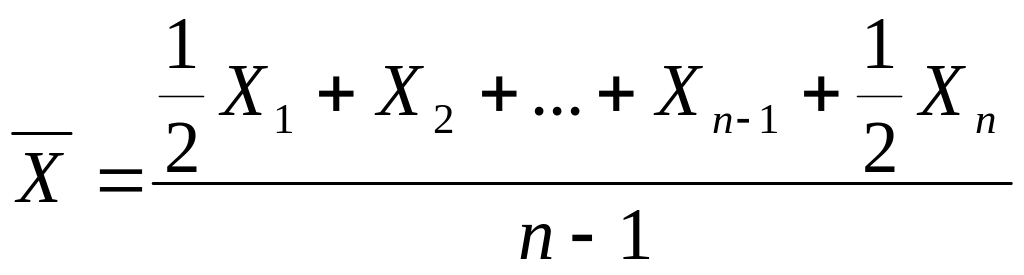(5.9)
Все остальные средние показатели для интервальных и моментных рядов динамики рассчитываются одинаково.
Обобщающим
показателем скорости изменения явления
во времени является средний абсолютный
прирост (
).
Для его определения используется
формула средней арифметической простой
и ее преобразование в ряду динамики
.
(5.10)
Средний темп роста
(
)
определяется по формуле средней
геометрической из темпов роста,
исчисленных с переменной базой сравнения
,
(5.11)
где
.
Средний темп
прироста (
)
вычисляется исходя из среднего темпа
роста:
.
(5.12)
Средняя величина
одного процента прироста (
)
исчисляется делением среднего абсолютного
прироста на средний темп прироста:
. (5.13)