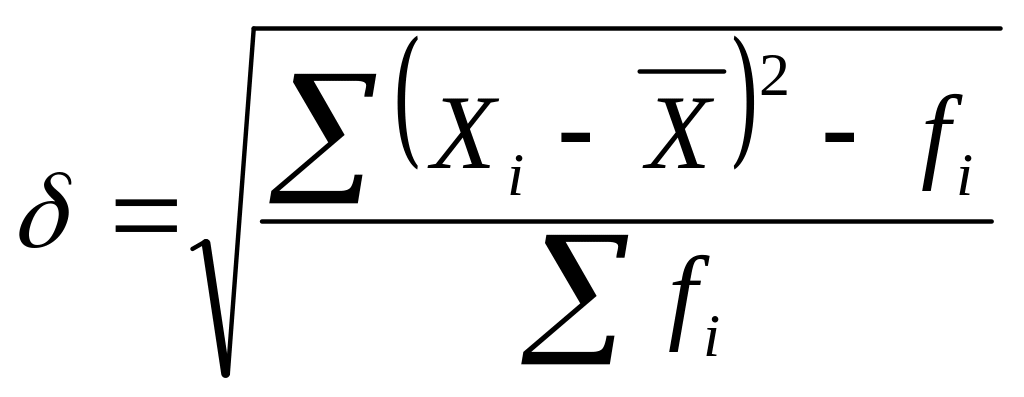- •Оглавление
- •Раздел 1. Описательная и аналитическая статистика на автомобильном транспорте
- •Статистическое наблюдение
- •Сводка и группировка статистических материалов
- •3. Абсолютные и относительные статистические величины
- •4. Средние статистические величины и показатели вариации
- •5. Ряды динамики и их анализ
- •6. Индексы
- •7. Выборочное наблюдение
- •8. Статистическое изучение взаимосвязи социально-экономических явлений
- •Раздел 2. Статистика автомобильного транспорта
- •16. Статистика финансовых результатов деятельности автотранспортного предприятия
- •Введение
- •Раздел 1. Описательная и аналитическая статистика на автомобильном транспорте
- •1. Статистическое наблюдение
- •1.1. Сущность статистического наблюдения, программно-методологические вопросы статистического наблюдения
- •1.2. Основные организационные формы, виды и способы статистического наблюдения
- •Вопросы для самоконтроля
- •Практикум Задачи и упражнения
- •2. Сводка и группировка статистических материалов
- •2.1. Понятие сводки и группировки. Виды группировок
- •Группировочный признак, образование групп и интервалов в группировке
- •Статистические таблицы
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •3. Абсолютные и относительные статистические величины
- •3.1. Абсолютные статистические величины
- •3.2. Относительные статистические величины
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •4. Средние статистические величины и показатели вариации
- •4.1. Средние статистические величины: сущность, значение, виды и способы расчета
- •4.2. Показатели вариации
- •Задания для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельной работы
- •5. Ряды динамики и их анализ
- •5.1. Виды рядов динамики, методы расчета показателей ряда динамики
- •5.2. Выявление основной тенденции развития показателя
- •5.3. Анализ сезонных колебаний
- •5.4. Экстраполяция в рядах динамики и прогнозирование
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •6. Индексы
- •6.1. Понятие и значение индексов, их классификация
- •6.2. Средние индексы
- •6.3. Преобразование агрегатных индексов
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •7. Выборочное наблюдение
- •7.1. Понятие о выборочном наблюдении и его теоретические основы
- •7.2. Способы и виды выборки
- •Вопросы для самоконтроля
- •Практикум Задачи с решением
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •8. Статистическое изучение взаимосвязи социально-экономических явлений
- •8.1. Способы выявления связей между показателями
- •8.2. Парная регрессия
- •8.3. Многофакторная регрессия
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 2. Статистика автомобильного транспорта
- •9. Статистика перевозок грузов и пассажиров
- •9.1. Статистика грузовых перевозок
- •9.2. Статистика пассажирских автобусных перевозок
- •Автобусные перевозки
- •Перевозки маршрутными (сдельными) автобусами
- •Перевозки заказными (повременными) автобусами
- •9.3. Статистический анализ объема перевозок
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •10. Статистика основных фондов (средств) автотранспортного предприятия
- •10.1. Статистика наличия и состава основных фондов
- •10.2. Статистика движения и состояния основных фондов
- •10.3. Статистика транспортных средств
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •11. Статистика оборотных средств автотранспортного предприятия
- •11.1. Статистика наличия, состава и эффективности использования оборотных средств
- •11.2. Статистическое изучение использования материальных ресурсов
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •12. Статистика трудовых ресурсов предприятия автомобильного транспорта
- •12.1. Статистика состава и численности работающих
- •12.2. Статистика движения персонала
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •13. Статистика использования рабочего времени
- •13.1. Рабочее время и задачи его статистического изучения
- •13.2. Статистическое изучение рабочего времени в человеко-днях
- •13.3. Статистика использования рабочего времени в человеко-часах
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •14. Статистика оплаты труда
- •14.1. Статистика фонда заработной платы
- •Статистика уровня и динамики заработной платы
- •. Индексный метод анализа заработной платы
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •15. Статистика себестоимости перевозок грузов и пассажиров
- •15.1. Показатели себестоимости перевозок и задачи ее статистического изучения
- •15.2. Оценка выполнения плана и динамика себестоимости перевозок
- •15.3. Статистические методы выявления резервов снижения себестоимости перевозок
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •16. Статистика финансовых результатов деятельности автотранспортного предприятия
- •16.1. Система показателей финансовых результатов деятельности предприятия и задачи их статистического изучения
- •16.2. Статистическое изучение доходов, прибыли и рентабельности
- •Вопросы для самоконтроля
- •Практикум Задачи с решениями
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тестовые задания для проверки знаний
- •Раздел 1. Описательная и аналитическая статистика на автомобильном транспорте
- •Раздел 2. Статистика автомобильного транспорта
- •Список литературы
- •625000, Тюмень, у. Володарского, 38
- •6 25039, Тюмень, ул. Киевская, 52
4.2. Показатели вариации
Вариация используется для подтверждения надежности средней величины и определения степени риска. Средняя величина, обобщающая результаты статистического наблюдения, не показывает, как колеблются вокруг нее индивидуальные значения признака, поэтому возникает необходимость изучения вариаций.
Вариацией называется различие значений признака у отдельных единиц совокупности. Например, отдельные ремонтные рабочие имеют разную месячную заработную плату, которая отличается от средней заработной платы. Вариация возникает в силу того, что отдельные значения признака формируются под влиянием большого числа взаимосвязанных факторов. Эти факторы часто действуют в противоположных направлениях, и их совместное действие формирует значение признаков у конкретной единицы совокупности.
Для характеристики размера вариации используются специальные показатели вариации:
- размах вариации;
- среднее линейное отклонение;
- среднее квадратическое отклонение;
- дисперсия;
- коэффициент вариации.
Размах вариации является простейшим показателем вариации и рассчитывается по формуле
R=Xmax-Xmin (4.9)
Недостаток этого показателя заключается в том, что он зависит только от двух крайних значений признака (максимального и минимального) и не характеризует колеблемости внутри совокупности.
Более точную характеристику колеблемости дают показатели: среднее линейное отклонение и среднее квадратическое отклонение. Они показывают, насколько в среднем отличаются индивидуальные значения признака от среднего его значения, и являются именованными числами, характеризуя абсолютную меру вариации.
Средние линейные отклонения берутся по абсолютной величине, т.к. в противном случае, из-за математических свойств средней величины, они всегда были бы равны нулю. Расчет показателей среднего линейного отклонения и среднего квадратического отклонения в зависимости от способа представления исходной информации рассчитывают по формулам, представленным в таблице.
Таблица 4.1
Наименование показателя |
Представление информации |
|
несгруппированные данные |
сгруппированные данные |
|
Среднее линейное отклонение, d |
|
|
Среднее квадратическое отклонение,
|
|
|
На практике чаще используется среднее квадратическое отклонение. Среднее линейное отклонение и среднее квадратическое отклонение нельзя непосредственно использовать для сравнения степени вариации по одному и тому же признаку в двух группах с разным уровнем средних, а также для сравнения вариации двух различных признаков в одной группе.
Кроме рассмотренных показателей, для измерения вариации используют дисперсию (σ2). Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
В зависимости от представления исходной информации дисперсия рассчитывается по формулам простой и взвешенной дисперсий:
![]() (простоя дисперсия); (4.10)
(простоя дисперсия); (4.10)
![]() (взвешенная дисперсия). (4.11)
(взвешенная дисперсия). (4.11)
Дисперсия и среднее квадратическое отклонение связаны между собой
![]() .
(4.12)
.
(4.12)
Наиболее часто в практических расчетах применяют относительный показатель вариации – коэффициент вариации.
Коэффициент вариации (V) показывает, на сколько процентов в среднем индивидуальные значения отличаются от средней величины, и определяется как отношение среднего квадратического отклонения к средней величине признака
![]() .
(4.13)
.
(4.13)
Коэффициент вариации характеризует количественную однородность статистической совокупности. Если данный коэффициент < 33%, то это говорит об однородности статистической совокупности и надежности средней величины, которую можно использовать в дальнейших расчетах.