Первое уравнение максвелла и закон полного токa
На оснований уравнений
В =
rot rotA = µ δ
можно записать, что
rotB = µ δ.
Делим обе части равенства на скалярную величину µ - абсолютную магнитную проницаемость среды и вводим обозначение
-
вектор напряжённости магнитного поля.
Тогда
rotH = δ. (61)
Это первое уравнение Максвелла в дифференциальной форме или закон полного тока в дифференциальной форме. Физический cмысл этого уравнения заключается в том, что в любой точке пространства, где существует электрический ток, имеется вихревое магнитное поле.
Проинтегрируем уравнение (61) по поверхности S (рис. 25):
ds
=
ds
=
i
и применим теорему Стокса,
d
=
dl
Рис. 25
Получаем
dl = i……………(62)
закон полного тока в интегральной форме или первое уравнение Максвелла в интегральной форме. Линейный интеграл напряженности магнитного поля по замкнутому контуру равен величине полного тока, проходящего через поверхность, ограниченную данным контуром.
Ротор – это функция, характеризующая поле в рассматриваемой точке пространства в отношении способности к образованию вихрей.
Уравнение (61) записано в общей форме безотносительно к системе координат, и в каждой конкретной системе координат оно раскрывается по своему. Например, в декартовой системе координат
rotH
=
.
Вихревыми
принято называть поля, в которых ротор
векторной величины, описывающей поле,
отличен от нуля. Так как для магнитного
поля постоянного тока rotH
= δ,
то
во всех точках пространства, где δ
0, поле вектора Н
является вихревым.
В областях пространства, где δ = 0, rotH = 0, магнитное поле можно рассматривать как потенциальное и для его характеристики можно ввести скалярный потенциал магнитного поля.
СКАЛЯРНЫЙ ПОТЕНЦИАЛ МАГНИТНОГО ПОЛЯ
В области, где нет токов (rotH = 0, δ = 0) следовательно, магнитное поле имеет смешанный характер и обладает, кроме векторного, также и скалярным потенциалом φm. Можно считать, что
H
=
-
………………………(63)
Т.к.
линии магнитной индукции непрерывны,
div
=0,
то при неизмененной магнитной проницаемости
µ=const,
непрерывны и линии напряженности
магнитного поля
divH = 0........................ (64)
Из (63) и (64) получается уравнение Лапласа
divgrad
=
0,
или
=0.
…(65)
Т.к. H является градиентом , то линии B и H должны быть н о р м а л ь н ы к поверхностям равного скалярного магнитного потенциала. В двухмерном поле линии магнитной индукции совпадают с их линиями равного векторного потенциала. Поэтому в двухмерном поле линии равного векторного и равного скалярного потенциала образуют ортогональную сетку, т.е. пересекаются под прямим углом.
Следует различать понятия падение магнитного напряжения и магнитное напряжение. Первое определяется только линейным интегралом от произведения Н на dl по выбранному пути. Второе – не только эти интегралом, но и магнитодвижущей силой (МДС), имеющейся на пути.
МАГНИТНОЕ ПОЛЕ НА ГРАНИЦЕ ДВУХ СРЕД
Т.к. линии магнитной индукции непрерывны, то нормальные к поверхности раздела сред составляющие вектора магнитной индукции не изменяются при переходе ив одной среды в другую (рис 26):
d
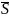=0;
Bсos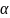
-
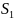сos
=0
Рис. 26
Т.к.
=
;
то
Cos
=
Cos
;…………(66)
=
…………………(67)
Согласно
первому уравнению Максвелла в области,
где
нет токов rot
=
0, следовательно, касательная составляющая
вектора Н
не должна изменяться на границе двух
сред:
d
=0;
sin
dl
-
sin
dl=0
ab = cd = dl; sin = sin …………………(68)
H1t = H2t………………………(69)
Разделив (67) и (69) получаем закон преломления магнитных линий на границе двух сред.
=
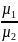………………………(70)
Таким образом, на границе двух сред с различными магнитными проницаемостями выполняются следующие граничные условия:
= , H1t = H2t. (71)
Чем
больше магнитная проницаемость, тем
под большим углом к нормали идут линии
поля. Если
,
то угол преломления
будет очень мал при любом угле падения
.
Если
первая среда сталь с магнитной
проницаемостью
=1000
а
вторая воздух
),
то магнитные линии из стали выходят
нормально к её поверхности:
=89
;
=3
20’.
МАГНИТНОЕ ПОЛЕ В ДИЭЛЕКТРИКЕ НА ГРАНИЦЕ
ИДЕАЛЬНОГО ПРОВОДНИКА С ТОКОМ
Идеальный проводник обладает бесконечно большой удельной проводимостью. Вследствие сил взаимного отталкивания заряды в толще идеального проводника сохраняться не могут, на встречая никакого сопротивления мгновенно всплывают на поверхность. Ток в идеальном проводнике можно представить как движение зарядов в очень тонкой поверхностной пленке. Для количественной оценки вводится понятие поверхностной плотности тока, измеряемой в амперах на погонный метр.
Вычислим циркуляцию вектора Н по малому контуру, одна сторона которого лежит в диэлектрике у поверхности идеального проводника, а другая в толще проводника (рис. 27)
=
ds
Внутри идеального проводника ток не течет и магнитного поля не существует.
Рис. 27
Т. к. линии напряженности магнитного поля непрерывны, то поле войти извне внутрь не может, следовательно, нормальной составляющей напряженности с внешней стороны проводника также не может быть. Получаем
dl = Hdx,
где Н – напряженность магнитного поля в диэлектрике у границы проводника. Вектор Н касателен к поверхности проводника, следовательно
H
=
=
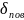. ………(72)
Линии магнитной индукции параллельны поверхности идеального проводника с током и нормальны к векторам поверхностной плотности тока.