Электрическое смещение и постулат максвелла

Поток вектора напряжённости электрического поля Е через любую замкнутую поверхность создается не только суммой свободных зарядов q_св, но и суммой связанных зарядов q_связ, находящихся внутри этой поверхности. Поэтому теорему Гаусса можно записать в следующем виде:

,

где .

Тогда

.

Объединяем интегралы, т.к. они берутся по одной и той же поверхности:

.

Под интегральное выражение представляет собой векторную величину, обозначим её буквой D и назовём вектором электрического смещения или вектором электрической индукции

; (13)

– вектор электрического смещения в пустоте.

Учитывая эти обозначения, запишем

. (14)

Выражение (14) носит название постулата Максвелла. Оно справедливо для любых полей (не только электростатического) и говорит о том, что поток вектора электрического смещения сквозь любую замкнутую поверхность равен свободному электрическому заряду, заключенному в объёме, ограниченном этой поверхностью.

Вектор не зависит от свойств среды и поэтому удобен для расчётов. Связь его с вектором легко получить из равенства

, (15)

откуда

.

ТЕОРЕМА ГАУССА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ

Для того чтобы судить о распределении зарядов внутри некоторой поверхности S нужно применить теорему Гаусса к элементарным зарядам ∆q_св , заключенным в объёме ΔV, ограниченном поверхностью Δ S (рис. 12). Чем меньше будет , тем точнее будет получена картина распределения зарядов:

Рис. 12

Делим обе части равенства на объём ∆V, ограниченный элементарной поверхностью ∆ S и переходим к пределу ∆V→0:

Левая часть равенства представляет собой дивергенцию вектора напряженности электрического поля E:

. (16)

Дивергенцией или расходимостью вектора называется предел отношения или полного потока вектора через замкнутую поверхность к объёму, ограниченному этой поверхностью, при бесконечном уменьшении последнего.

Правая часть равенства

Таким образом, получаем запись теоремы Гаусса в дифференциальной форме.

. (17)

В точках, где сосредоточен положительный заряд ( >0) находится источник поля (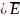 >0), в точках, где <0, находится сток – дивергенция отрицательна. В точках, где заряд отсутствует =0, divE = 0, нет ни источника поля, ни его стока, поле является трубкообразным – соленоидальным ( рис. 13).

Рис. 13

ВЫРАЖЕНИЕ ДИВЕРГЕНЦИИ В ДЕКАРТОВОЙ

СИСТЕМЕ КООРДИНАТ

Вектор Е в декартовой и декартова система координат запишется как , где i, j, k – единичные вектора (орты).

Рассмотрим поток вектора E через параллелепипед со сторонами dx, dy и dz (рис. 14).

Рис. 14

Считаем, что у задней стенки составляющая вектора по оси х равна , а у передней стенки , тогда поток, входящий в заднюю стенку, равен , а поток, выходящий через переднюю стенку, равен .

Разность этих потоков представляет собой поток, возникающий в объёме, ограниченном поверхностью параллелепипеда. Он равен

Аналогично можно получить приращения потока по осям y и z. Полное при приращение потока равно алгебраической сумме приращений потоков по отдельным осям

.

Разделив , получаем выражение дивергенции

. (18)

Для упрощения записи вводится дифференциальный векторный оператор Гамильтона – набла

. (18а)

Сравнивая выражения(18) и (18а) легко увидеть, что дивергенция вектора равна скалярному произведению наблы на сам вектор.

. (18б)

Убедиться в этом представляем самим читателям. При умножении обращайте внимание на то, что скалярное произведение ортов самих на себя равно единице, а друг на друга нулю.

Таким образом, теорему Гаусса в дифференциальной форме можно записать и так

(19)

Если учесть влияние поляризации появлением связанного заряда q_связ на границе диэлектрика, то можно считать, что поле существует в вакууме, но создаётся как свободным q_св, так и связанным зарядом:

.

Следовательно, истоком вектора Е являются как свободные, так и связанные заряды.

Также как и теорему Гаусса, постулат Максвелла можно записать в дифференциальной форме

. (20)

Следовательно, истоком вектора D являются свободные заряды.

ТЕОРЕМА ОСТРОГРАДСКОГО

Теорема Остроградского даёт связь между объёмным и поверхностным интегралами для любых векторов, непрерывных в области V и на ограничивающей её поверхности S. Для любого вектора А справедливо равенство

(21)

Действительно, divAdV представляет собой поток вектора из элемента объема. Сумма потоков через все внутренние элементы равна нулю, т.к. в один элемент поток входит, а из другого выходит. Остается поток через внешние элементы, который и является потоком через внешнюю поверхность S, т.е. равен левому интегралу.

УСЛОВИЕ ПОТЕНЦИАЛЬНОСТИ ПОЛЯ. РОТОР

Понятие потенциала было введено на основании того, что работа сил поля не зависит от пути, т.е. что циркуляция равна нулю . Поле потенциально в любой точке, если циркуляция вдоль любого малого контура равна нулю.

Пусть малый контур охватывает элементарную площадку (рис. 15).

Рис. 15

Введем понятие «ротора» или вихря вектора. Ротор – это функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей. Из курса математики известно, что составляющая ротора по нормали к выбранной площадке равна пределу отношения циркуляции вектора к величине площадки при бесконечном уменьшении последней:

.

При соответствующем выборе вектора ∆s можно записать, что

rotE = 0. (22)

Поле будет потенциальным, если в любой точке его

Уравнение (22) записано в общей форме безотносительно к системе координат, и в каждой конкретной системе координат оно раскрывается по-своему.

В декартовой системе координат составляющие вектора А по координатам х, у, z записываются в следующем виде:

= ;

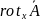= ; = . . . . (23)

Ротор равен геометрической сумме составляющих.

ЭЛЕКТРИЧЕСКАЯ ЁМКОСТЬ

Электрическая ёмкость С уединенного проводника – это скалярная величина, характеризующая способность проводника накапливать электрический заряд. Ёмкость равна отношению заряда к потенциалу проводника, в предположении, что все остальные проводники удалены в бесконечность и их потенциалы равны нулю:

C = . (24)

Ёмкость зависит от работы, которую затратили для того, чтобы зарядить тело, т.е. от размеров и формы тела и от свойств окружающей среды.

Электрическая ёмкость между двумя проводниками, имеющими одинаковые по величине, но противоположные по знаку заряды, или ёмкость конденсатора, равна абсолютному значению отношения заряда на одном из тел к напряжению между телами:

C = . (25)

Ёмкость конденсатора зависит от геометрии, размеров и взаимного расположения тел, а также от абсолютной диэлектрической проницаемости диэлектрика. Если ε = const, то ёмкость не зависит от q и U.

УРАВНЕНИЯ ПУАССОНА И ЛАПЛАСА

Эти уравнения являются основными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме

divE = div (-gradφ) = (26)

или

∇(∇φ) = ∇²φ = Δφ = - , (27)

где Δ – векторный оператор Лапласа или лапласиан.

Уравнение (27) называют уравнением Пуассона. Частный вид уравнения Пуассона, когда ρ_св = 0, называют уравнением Лапласа:

Δφ = 0.

В декартовой системе координат уравнение Пуассона записывают следующим образом:

. (28)

Уравнение Пуассона выражает связь между частными производными второго порядка от φ в любой точке поля и объёмной плотностью свободных зарядов в этой же точке поля. В тоже время потенциал в какой либо точке поля зависит от всех зарядов, создающих поле, а не только от значения свободного заряда, находящегося в данной точке.

ГРАНИЧНЫЕ УСЛОВИЯ

Под граничными условиями понимают условия, которым подчиняется поле на границах раздела сред с разными электрическими свойствами. Электрическое поле описывается уравнениями Пуассона или Лапласа. Это уравнения в частных производных, которые имеют в общем случае множество линейно независимых друг от друга решений. Выбор единственного, удовлетворяющего конкретной задаче, и производят с помощью граничных условий.

Граничные условия на границе проводник-диэлектрик.

В проводнике, находящемся в электростатическом поле, вследствие явления электростатической индукции, происходит разделение зарядов, которые распределяются в тонком приповерхностном слое с поверхностной плотностью заряда σ (рис. 16).

Поверхность тела эквипотенциальна, вектор напряжённости внешнего электрического поля в любой точке поверхности подходит к ней под прямым углом.

Рис. 16

Внутри проводящего тела напряжённость поля равна нулю, так как внешнее поле компенсируется полем зарядов, расположенных на поверхности тела. Поэтому на границе раздела проводник-диэлектрик выполняются два условия:

E_t = 0; D = σ.

Граничные условия на границе диэлектрик-диэлектрик.

На границе раздела двух диэлектриков с различными диэлектрическими свойствами выполняются два следующих условия:

E_1t = E_2t ; D_1n = D_2n.

При наличии на границе раздела двух сред свободных зарядов с плотностью σ выполняется равенство

D_2n – D_1n = σ.

При переходе через границу раздела двух диэлектриков потенциал не претерпевает скачков.

ПОТЕНЦИАЛЬНЫЕ КОЕФФИЦЕНТЫ

Потенциал каждого тела определяется не только его зарядом, но и зарядом остальных тел.

……………………………………… (29)

Коэффициенты с одинаковыми индексами носят название собственных потенциальных коэффициентов, с различными 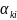- взаимных. Необходимо заметить, что от перестановки индексов величина потенциального коэффициента не изменится ( , т.к. энергия системы заряженных тел не зависит от порядка ее заряда.

РЕШЕНИЕ ЗАДАЧ ЭЛЕКТРОСТАТИКИ

В зависимости от того, что задано и что определяют, задачи электростатики можно подразделить на три вида:

- по заданному закону распределения потенциала в пространстве φ(x, y, z) найти распределение свободных зарядов, вызвавших поле;

- задан закон распределения свободных зарядов в пространстве в функции координат ρ(x, y, z), найти закон изменения в пространстве φ(x, y, z);

- известны потенциалы или полные заряды и геометрия тел, создающих поле; требуется найти закон изменения Е или φ во всех точках поля.

В простых случаях задача расчета поля может быть решена с помощью теоремы Гаусса. Чтобы ею воспользоваться часто бывает удобно заменить эквипотенциальную поверхность бесконечно тонким проводящим листом.

Непосредственное интегрирование уравнений Пуассона и Лапласа может быть произведено элементарными приемами, если имеется лишь одна независимая переменная. При сложной форме поля уравнение Пуассона и Лапласа интегрируется с помощью специальных приемов, например, методом Фурье-Ламе.

Расчет плоскопараллельных полей , независящих от третьей координаты может быть произведен при помощи функций комплексного переменного – методом конформных отображений.

Расчет можно выполнить также методами наложения, в том числе методом участков; зеркальных изображений; средних потенциалов – метод (для упрощения вводится предположение о том, что на проводниках заряд распределен равномерно, а потенциал различных точек проводника неодинаков); потенциальных коэффициентов; графическое построение картины поля; разностных уравнений – метод сеток; интегрирование уравнений Лапласа и Пуассона специальными интеграторами; моделирование поля.

Задача должна быть решена единственным образом с тем, чтобы

удовлетворять следующим условиям:

- уравнениям поля

rotE = 0; D = ε E; divD = ρ;

первое из этих уравнений rot E = 0 эквивалентно равенству

;

уравнения сводятся к уравнениям Пуассона или Лапласа

или ;

- поверхности проводящих тел должны быть эквипотенциальны;

- потенциалы на поверхностях проводящих тел должны быть равны заданным U_k. Если заданы полные заряды тел, то для каждого тела должно быть выполнено условие:

.

ЭНЕРГИЯ СИСТЕМЫ ЗАРЯЖЕННЫХ ТЕЛ

Система заряженных тел является носителем определённого запаса энергии. Эта энергия сообщается системе внешними источниками в процессе образования зарядов и может быть вновь возвращена или преобразована в другие виды при уменьшении зарядов.

Рассмотрим работу, совершаемую внешними источниками при образовании зарядов. Для k-того тела

dA_k=φ_k dq_k ; A_k = .

Для всех n тел

A = .

Считаем, что заряд производится бесконечно долго, тогда можно пренебречь потерями в проводниках и считать накопленную в электростатическом поле энергию равной работе внешних источников.

=А.

Потенциал каждого тела определяется зарядами всех тел

= + +…+ ,

где - потенциальные коэффициенты.

Порядок установления зарядов не влияет на величину накопленной в системе энергии.

Если бы это было не так, то можно было бы заряжать систему в одном порядке, разряжать в другом и в результате получать энергию. Таким образом получился бы вечный двигатель, что противоречит закону сохранения энергии.

Для удобства вывода считаем, что заряды тел устанавливаются пропорционально друг другу, т.е. что = .

Тогда

= + …+ =( …+ ) .

Потенциал тела в этом случае будет пропорционален его заряду:

;

где mk= +…+ .

Энергия

=A= d = d = ;

= ; (30)

Энергия системы заряженных тел равна полусумме произведений потенциалов тел на их заряды.

Для конденсатора, состоящего из двух обкладок, энергия равна

= + ;

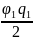т.к. = q, а = - q; то = ( - 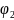); обозначив - =u; имеем = ; учитывая, что q = CU или U=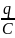 ; получаем энергию конденсатора в виде

= = = . (31)

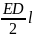Остановимся еще раз на распределении энергии в электрическом поле. Обозначим - объемную плотность энергии - энергию, заключенную в единице объема поля. В однородном поле плоского конденсатора заключено энергия = . Как известно, q = σS = DS, а U = E , т.е. = S; V- объем поля. Тогда = = ; D = εE.

В очень малом объеме любое поле считать однородным и вычислить :

= = = ; (32)

Энергия, заключенная в объеме

= dV. (33)

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАРЯЖЕННЫЕ ТЕЛА.

Силы взаимодействия между заряженными телами, которые нельзя рассматривать как точечные, могут быть вычислены как производные энергии системы по обобщенной координате.

Как известно из механики, наименьшее число обобщенных координат, необходимое для определения положения системы, равно числу степеней свободы системы.

Рассмотрим систему, состоящую из n заряженных тел. Для того, чтобы выяснить, какая сила действует на одно из тел, нужно положить, что все тела жестко закреплены, и рассматриваемое тело может перемещаться только так, что изменяется одна его координата (рис. 17).

Рис. 17

Это изменение координаты совершается под действием силы f, являющейся результатом взаимодействия рассматриваемого тела со всеми другими заряженными телами.

Работа внешних источников идет на приращение энергии системы и на механическую работу (считаем, что потерь нет):

d =d +fdg; (34)

d - приращение энергии системы при изменении координаты g.

Рассмотрим случай, когда заряды всех тел остаются неизменными, =const. Практически это означает, что все тела отключены от источников, d =0 и работа внешних сил равна нулю, т.е. fdg= -d . Знак минус показывает, что если работа производится силами поля, что энергия поля убывает.

Механическая сила

f= - = const (35)

Механическая сила, стремящаяся изменить данную координату, равна убыли энергии электрического поля, отнесенной к единице производимого силой изменения данной координаты, в предположении, что заряды всех тел остаются неизменными.

Рассмотрим другой случай, когда все тела подключены к внешним источникам и потенциалы их неизменны =const.

Как было доказано раньше, энергия системы заряженных тел = . Ёе приращение при =const d = равно половине работы внешних источников.

Таким образом, из (35) следует, что в этом случае fdg=d . При перемещении под действием сил поля энергия увеличивается.

Сила

f = + = const. (36)

Оба выражения для сил торжественно равны друг другу. Покажем это, взяв в качестве примера конденсатор. Положим q=const

= = ;

тогда

f = - = - = ; т.к. = U; то f = .

Положим теперь, что U = const, тогда f = = .

Оба выражения одинаковы, они показывают, что механические силы, действующие на обкладке конденсаторов, стремится их сблизить, т.е. увеличить ёмкость конденсатора.