2.(10) Изображение плоских и пространственных фигур в параллельной проекции.

Паралельное проектирование. Возьмем в евклидовом пространстве Е₃ некоторую плоскость σ и какой-нибудь ненулевой вектор , не параллельный этой плоскости.

Пусть - произвольная точка пространства. Проведем через эту точку прямую, параллельную вектору , и обозначим через А₀ точку, в которой эта прямая пересекает плоскость σ. Точка А₀ называется проекцией точки на плоскость σ при праектировании паралельно вектору . Обычно предполагается, что плоскость σ и вектор заданы, поэтому точку А₀ кратко называют параллельной проекцией точки . Если вектор перпендикулярен к плоскости σ, то точка называется ортогональной проекцией точки . Множество параллельных проекций всех точек фигуры образуют некоторую фигуру F₀, которая называется параллельной проекцией фигуры . Если вектор перпендикулярен к плоскости σ, то F₀ называется ортогональной проекцией фигуры .

Свойства. (Прямые и отрезки не параллельны вектору )

1. Проекция прямой есть прямая.

2. Проекции паралельных прямых параллельны и совпадают.

3. Проекция отрезка 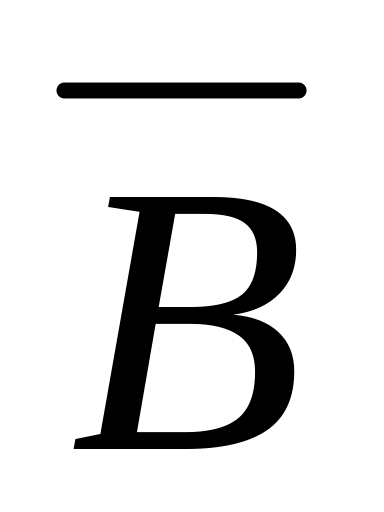есть отрезок А₀ B₀, где А₀ и B₀– проекции точек и .

4. При параллельном проектировании сохраняется простое отношение трех точек; в частоности, проекция середины отрезка есть середина проекции отрезка.

5. Проекции параллельных отрезков параллельны и принадлежат одной прямой.

6. Проекции параллельных отрезков или отрезков, лежащих на одной прямой, пропорциональны самим отрезкам.

Пусть σ’ и σ — различные или совпадающие плоскости пространст­ва Е₃. Взаимно однозначное отображение f:σ’ σ называется аф­финным отображением плоскости σ’ на плоскость σ’, если оно любые три точки М’₁, M’₂, М’₃ плоскости σ’, лежащие на одной прямой, пере­водит в три точки М₁, M₂, М₃ плоскости σ, лежащие на одной прямой, и сохраняет их простое отношение, т. е. (М’₁M’₂, М’₃ ) = (М₁M₂, М₃). Отображение f:σ’ σ называется подобием, если существует такое число k > 0, что для любых двух точек A’ и B’ плоскости σ’ и их обра­зов А и В плоскости σ выполняется равенство АВ = kA’B’. Аффинное отображение f:σ’ σ будет, очевидно, аффинным пре­образованием, если плоскости σ’ и σ совпадают. Таким образом, аффинные преобразования являются частным случаем аффинных отображений.

Теорема 1. Пусть R’ = (А’, В’, С’) и R = (А, В, С) — произволь­ные реперы соответственно плоскостей σ’ и σ. Тогда существует одно и только одно аффинное отображение плоскости σ’ на плоскость σ, ко­торое переводит репер R’ в репер R. При этом любая точка М’ пло­скости σ’ с данными координатами в репере R’ переходит в точку М плоскости σ с теми же координатами в репере R.

Фигуры F’ и F, лежащие соответственно в плоскостях σ’ и σ, назы­ваются аффинно-эквивалентными, если существует аффинное отоб­ражение f:σ’ σ которое фигуру F’ переводит в фигуру F. Если, в частности, существует подобие f, при котором F = f(F’), то фигуры F’ и F называются подобными.

Теорема 2. Два четырехугольника, лежащие соответственно в плоскостях σ’ и σ, аффинно-эквивалентны тогда и только тогда, когда их можно обозначить буквами A’B’C’D’ и ABCD так, чтобы (А’С’, Е’) = (AC, E), (B’D’, E’) = (BD, Е), где E’, Е — точки пересечения прямых A’C’, B’D’ и AC, BD

Выберем некоторую плоскость σ и назовем ее плоскостью изобра­жений. Затем возьмем ненулевой вектор , не параллельный пло­скости σ. Направление этого вектора назовем направлением проек­тирования. Пусть F’ — произвольная фигура, расположенная в пространстве, a F — параллельная проекция этой фигуры на плоскость σ. Фигуру F’ называют оригина­лом, a F — проекцией оригинала. Любую фигуру F₀ на плоскости σ, подобную фигуре F, называют изображением фигуры F’.

Построение изображений фигур с помощью параллельного проектирования основано на свой­ствах параллельного проектиро­вания и аффинных отображений. Будем предполагать, что плоскости оригинала и изображения пересе­каются и что направление проектирования не параллельно ни одной из этих плоскостей.

Теорема 3. Пусть фигуры F’ и F лежат соответственно на пересекаю­щихся плоскостях σ’ и σ. Фигура F может служить изображением фигуры F’ тогда и только тогда, когда фигу­ры F’ и F аффинно-эквиваленты.

а) Треугольник. Нетрудно видеть, что любой треугольник ABC плоскости σ может служить изображением данного треугольника A’B’C’ плоскости σ’, если плоскости σ’ и σ пересекаются. В самом деле, по теореме 1 существует аффинное отображение f:σ’ σ, которое репер (A’,B’,C’) переводит в репер (A,B,C), поэтому треуголь­ники A’B’C’ и ABC аффинно-эквивалентны. По теореме 3 треугольник ABC может служить изображением треугольника A’B’C’.

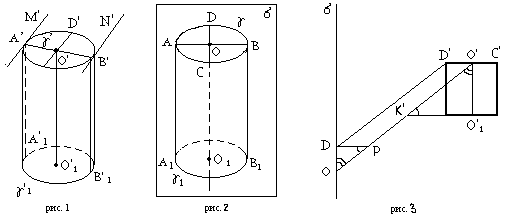
б) Цидиндр. Пусть данный цилиндр-оригинал F’ расположен так, что его ось О’O’₁ параллельна плоскости изображения σ. Направление проектирования выбрано следующим образом; оно не параллельно плоскостям оснований цилиндра, но параллельно плоскости, проходящей через ось цилиндра перпендикулярно к плоскости σ (для наглядности).

Пусть γ’ - окружность верхнего основания цилиндра F’, а A’B’ и C’D’ – взаимно перпендикулярные диаметры этой окружности, причем А’В’║σ . Проведем контурные образующие А’А’₁ и В’В’₁ цилиндра F’ и рассмотрим касательные А’М’ и В’N’ к окружности γ’ в точках А’ и В’. При проектировании цилиндра F’ на плоскость σ окружность γ’ проектируется в эллипс γ с осями АВ и CD, которые являются проекциями диаметров А’В’ и C’D’. Для большей наглядности изображение проектирования выбирается так, чтобы АВ>CD. Для этого достаточно, направление проектирования выбрать таким образом, чтобы прямая, проходящая через точку О’ по этому направлению, пересекала плоскость нижнего основания цилиндра в точке К’, что О’О’₁<О’₁К’ ( рис3., где изображено сечение цилиндра F’ плоскостью, проходящей через ось О’О’₁ перпендикулярно к плоскости σ ). Так как ▲ О’О’₁К’~▲ОDP, то OD<DP или OD<D’O’=OA. Т.о. 2OD<2OA или CD<AB. В этом случае АВ – большая ось эллипса γ, а CD –малая. Отрезок CD принадлежит проекции ОО₁, оси цилиндра. Так как плоскость, определяемая прямыми А’А’₁ и А’М’, перпендикулярна к плоскости σ, то проекции этих прямых совпадают. Но проекция АМ касательной А’М’ является касательной к эллипсу γ. Поэтому проекция АА₁ контурной образующей А’А’₁ является касательной к эллипсу γ. Аналогично проекция ВВ₁. Нижнее основание γ’₁ цилиндра проектируется в эллипс γ₁, равный эллипсу γ и полученный из него параллельным переносом на вектор . Ясно что прямые А₁А и В₁В являются касательными к эллипсу γ₁ в точках А₁ и В₁.