(Показат-ая ф-я рацион-го аргумента)

Пусть а – некот. заданное положит. действит-ое число. Выберем из мн-ва R рац-х чисел произ. число r и, зафиксировав его, рассм. степ. ф-ю y = F(x)=x^r.

Поставим выбранному r в соответ-е знач-е F(a)=a^r этой ф-ии(оно : для х=а>0 ф-я х^r определена при рац-ном r).Такое соответ-е м/о осущ-ть для кажд. r R. Тогда на мн-ве всех рац-х чисел построится некот. ф-я f(r) аргумента r, к-рая наз. показат-ой ф-ей рац-го аргумента и обозн. ч/з а^r: y = f(r)=a^r (a>0).

Рассм. некот. св-ва ф-ии f(r). б. предполагать, что а 1.

1) Ф-я f(r) положит-на при всяком r.

Действит-но, знач-е ф-ии f(r) в кажд. точке r есть знач-е ф-ии F(x)=x^r в точке х=а>0, а степ. ф-я х^r при х>0 принимает т/о положит. знач-я.

2) Для рац-х чисел r₁, r₂: а^r1∙a^r2= a^r1+r2 (1), a^r1:a^r2= a^r1-r2 (2), (a^r1)^r2= a^{r1 r2} (3).

Все 3 рав-ва док-ся аналог-но; докажем рав-во (1). Для целых знач-й r₁,r₂ оно очевидно. Пусть r₁= и r₂= - дробные положит-е числа; тогда а = а =a =

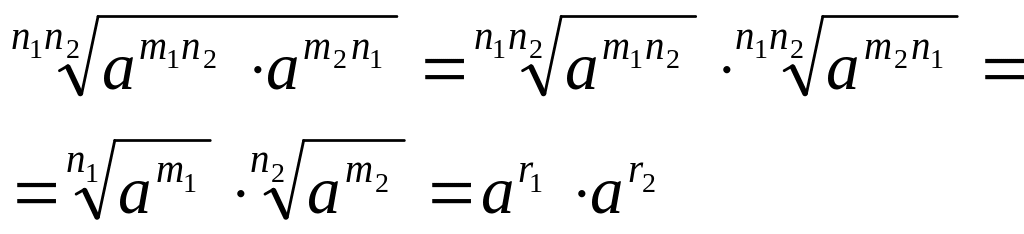
Заметим, что из рав-ва (3) следует (при r₁= -1, r₂=r):

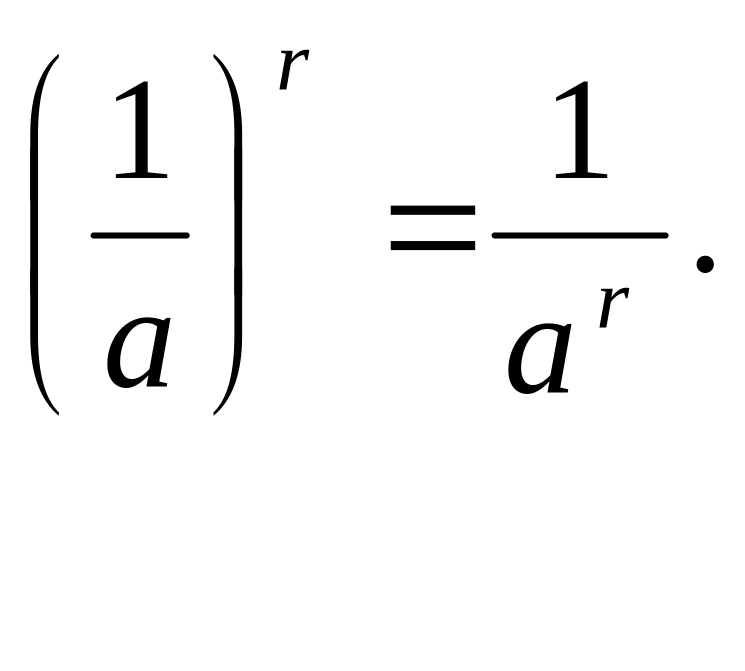
3) При а>1, f(r)>1, е/и r>0, и f(r)<1,е/и r<0.

Это вытекает из св-ва монотонности степ. ф-ии х^r на (0, +∞): е/и а и 1-два знач-я х, причем а>1, то при r>0, a^r>1^r=1,a при r<0, a^r<1^r=1.

Аналог-но док-ся, что при 0<a<1, f(r)<1, е/и r>0,и f(r)>1, е/и r<0.

4) При а>1 ф-я f(r)=a^r монотонно возрастает, а при 0<a<1- монотонно убывает на мн-ве всех рац-х чисел.

В с.д., пусть, напр., а>1и r₂>r_1, т.е. r₂-r₁>0, тогда по пред. св-ву, а^{r2 - r1}>1 или (по 2)) , откуда, умножая обе части этого нер-ва на а^r1, получим (по св-ву 1)): а^r2>a^r1, т.е. f(r₂)>f(r₁).

Аналог-но обнаруж-ся, что f(r)=a^r монотонно убывает при 0<a<1.

5) Пусть сначала а>1. Покажем, что в точке r=0 ф-я а^r имеет правый и левый пределы и что оба они равны 1.

А) Положим r>0. тогда по св-ву 3) а^r>1 и a^r-1>0.

Пусть ε>0 наперед задано. Докажем, что м/о подобрать натур. число n: а -1<ε (4). Обозн. а^1/n-1=y, тогда а=(1+y)ⁿ, причем y>0 (св-во 3)); отсюда согласно нер-ву Бернулли, а≥1+ny; y≤ Выбирая теперь n при условии: n> (5), мы получим: а значит, и y<ε,т.е. при усл-ии (5) вып-ся нер-во (4).

Остановимся на одном к.-л. фиксир. знач-ии n, удовлет-щем (5), напр. n=n₀=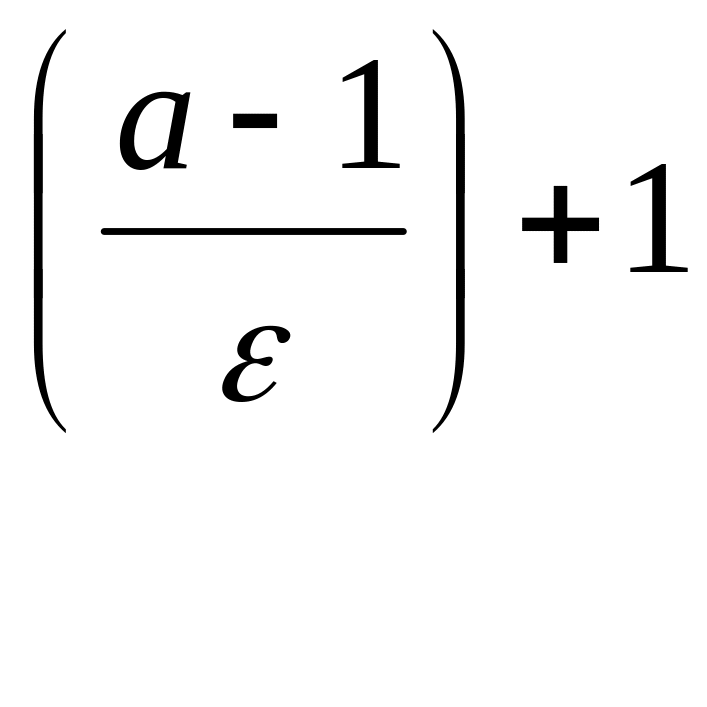 , и сопоставим число δ=1/n₀.Тогда, как т/о б. 0<r-0=r<δ, так тотчас же, в силу св-ва 4), окажется, что | а^r-1|=a^r-1<a^1/n0-1 или по 4) | a^r-1|<ε, а это и озн-т, что 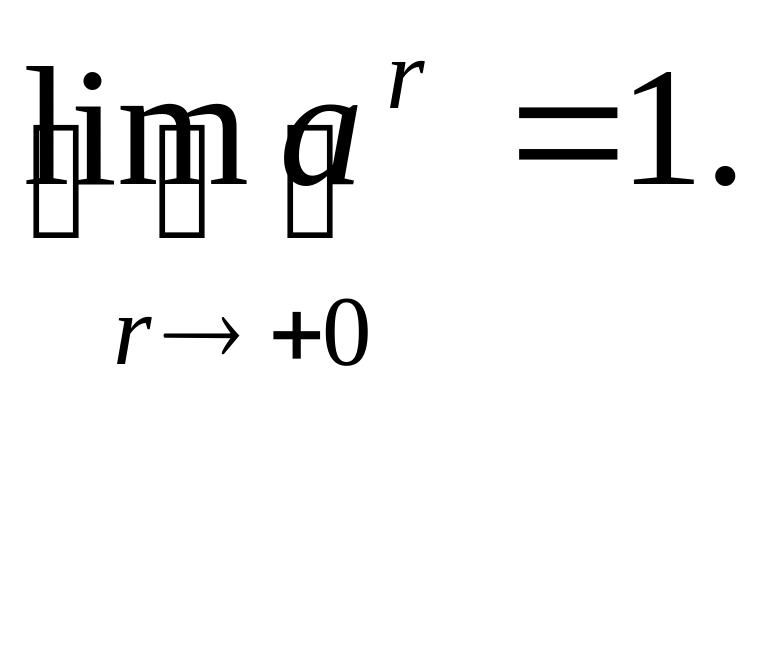Б) пусть теперь r<0. Положим r = -ρ, где ρ>0. Учитывая получим: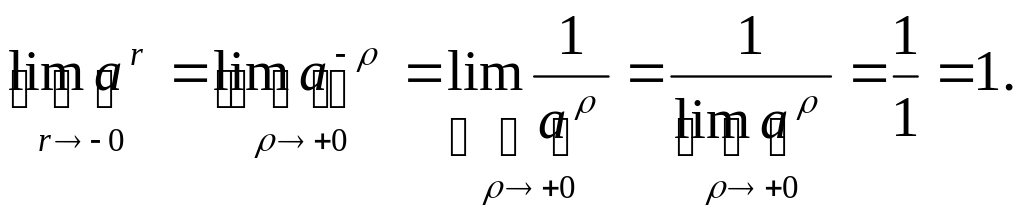

Итак, (а>1). Пусть теперь 0<a<1, тогда обозн. ч/з b дробь 1/а. Очевидно, что b>1. Поэтому снова получаем:

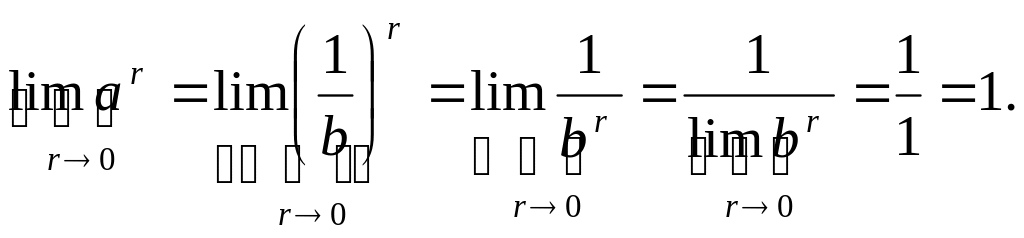
6) Показат. ф-я y = a^rнепр-на в кажд. рац-ной точке ρ.

Действит-но, а^r=a^ρ(a^r-ρ-1)+a^ρ. Но по св-ву 5)

(Показат. Ф-я произвольного действит-го аргумента)

Ч/ы построить эту ф-ю, введем пон-е ст-ни с иррац-ном показ-лем.

Пусть α-некот. иррац. число. Док-м, что (α>0-задано), предполагая сначало а>1. Заметим, что иррац. число α служит двусторонней предельной точкой для мн-ва рац-х чисел, т.е. в -окр-ти (α-δ,α+δ) точки α рац. числа: м/у числами α-δ и α, как и м/у числами α и α+β, всегда м/о найти рац. число. всегда м/о найти послед-ть рац-х чисел {r_n}, сходящуюся к α. При этом такая послед-ть м.б. выбрана как монот-но возр-щей, так и монот-но убыв-щей.

Сопоставляя окр-ти (α-δ_n, α+δ_n) (n=1,2,3,…),где послед-ть { δ_n}сх-ся к 0, мы м. выбирать числа r₁,r₂,…,r_n,… из полуокр-ти (α-δ_n,α) (или (α,α+δ_n)) и заботиться еще о том, ч/ы всякий раз, когда r_n уже выбрано (n=1,2,3…), δ_n+1 бралась еще при дополнит-ном ограничении: δ_n+1< α-r_n (δ_n+1<r_n- α). Тогда r_n+1 из полуокр-ти (α-δ_n+1, α) (или (α, α+δ_n+1)) б. заведомо >(<) r_n (n=1,2,3,…), и послед-ть r_n, сходящаяся к α, окажется монот-но возр-щей (убыв-щей).

Пусть теперь {r_n}-произвольная посл-ть рац-х чисел, сх-ся к α. Составим посл-ть {a^r }и док-м, что она сх-ся.

Т.к. посл-ть {r_n}сх-ся, то такое рац. число К, что r_n<K для -но (а>1), и Далее, (6)

Пусть ε>0 наперед задано. Т.к. то δ>0: при |r|<δ б. вып-ся нер-во (7) Но по критерию Коши м/о указать для нат. число N: m>N,n>N имеет место нер-во: |r_m-r_n|<ε` (8)

Возьмем в (8) ε`=δ, обозн. ч/з r=r_m-r_n. Тогда (8) примет вид: |r|<δ, а из него б. вытекать нер-во (7) с r=r_m-r_n: и получим по (6): (9) Итак нер-во (9) вып-ся, а это озн., что по критерию Коши посл-ть { }сх-ся:

Положим теперь, что {r^`_n}-к.-н. др. посл-ть рац-х чисел, также сх-ся к α. Тогда по доказ-му Докажем, что

Допустим от прот., что Составим посл-ть: r₁,r₁^{`</sup>,r<sub>2</sub>,r<sub>2</sub><sup>`},…,r_n,r_n<sup>`</sup>,…(10) помещая м/у кажд. 2-мя соседними членами r<sub>k</sub> и r<sub>k+1</sub> посл-ти {r<sub>n</sub>}член r<sub>k</sub>` посл-ти {r_n}. Ясно, что посл-ть (10) также сх-ся к α, и тогда соответ-щая посл-ть ст-ней д/а сх-ся. Но это невозм/о, т.к. ее посл-ти {a^r }и { }сх-ся к различ. пределам. Из всего сказ-го, по опр-ю предела ф-ии по Гейне

Е/и терерь 0<a<1, то положив 1/а=b, сведем ? о -нии к пред. сл-ю.

При а=1 : =

Итак, каковы бы ни были иррац. число α и число а>0, .Этот предел и приним-ся, по опр-ю, за ст-нь а^α с иррац. показ-лем α.

Теперь м/о кажд. х из (-∞, +∞) поставить в соответ-е !-ое число а^х. Тем самым на (-∞, +∞) построилась ф-я у=а^х (а>1). Эта ф-я и наз. показат-ой ф-ей действит-го аргум-та(показ-ой ф-ей).

Рассм. св-ва показ-ой ф-ии. Сл-й а=1 исключ-ся, т.к. в силу соотнош-я 1^х= ф-я у=1^х совпад-т с ф-ей у=1, св-ва к-рой тривиальны.

1) Ф-я у=а^х положит-на при

Для рац-х х это уже док-но. Пусть х=α-иррац. число. Сопоставим при а>1 монот-но возр-щую, а при а<1-монот-но убыв-щую посл-ть рац-х чисел {r_n}, сх-ся к α.

При а>1 ф-я а^r возр-т, и из r_n+1>r_n при а<1 ф-я а^r уже убывает, но теперь, по выбору посл-ти{r_n}, r_n+1<r_n, и значит снова так что в обоих сл-ях посл-ть монот-но возр-т. все члены этой посл-ти < ее предела а^α, и п.э. а^α> >0.

2) Для действит-х чисел х₁ и х₂ имеют место соотнош-я: (11) (12)

Док-во:Заметим, что принятое выше для иррац-го х в кач-ве опр-я рав-во: а^х= - остается, в силу непр-ти показ-ой ф-ии а^r рац-го аргум-та, верным и для рац-х х. Исходя из этого, докажем (12).Пусть {r_n}-к.-л. посл-ть рац-х чисел, сх-ся к х₁, а {r^{`</sup><sub>n</sub>}-посл-ть рац-х чисел, сх-ся к х<sub>2</sub>. Тогда и посл-ть {r<sub>n</sub>-r<sub>n</sub><sup>`}}рац-х чисел сх-ся и притом к числу х₁-х₂. В таком сл-е по т/о что сделанному замеч-ю Но из r_n x₁ следует: а из r_n^` x₂ вытекает: и значит, т.к. . Аналог-но док-ся рав-во(11).

Заметим, что из (12)(при х₁=0, х₂=х) рав-во Этим же методом предельного перехода док-ся и рав-во ( )

3) При действит. х: (1/а)^х=1/а^х.

В с.д.,

4) Е/и х>0, то а^х>1 при а>1 и а^х<1 при 0<a<1, е/и же х<0, то а^х<1 при а>1 и а^х>1 при 0<a<1.

Док-во:Пусть сначала х>0. Положим, что {r_n}- монот-но возр=щая посл-ть полож-х рац-х чисел, сх-ся к х. Составим посл-ть { }. Она сх-ся к а^х, причем е/и а>1, то эта посл-ть монот-но возр-т и тогда при n а^х> (13), е/и же 0<a<1, то она монот-но убыв-т, и тогда а^х< (14)

Но r_n>0 -но для а>1 и для а<1. В 1-ом сл-е отсюда следует (по (13)), что и а^х>1, а во 2-ом (по (14)), что а^х<1.

Е/и теперь х<0, то откуда по пред. при а>1(a<1) имеем: a^|x|>1 (a^|x|<1), и значит а^х<1 (a^x>1).

5)При а>1 ф-я а^х монот-но возр-т, а при 0<a<1-монот-но убывает на(-∞, +∞).

6)

7) Показ. ф-я а^х непр-на в кажд. точке.

Св-ва 5)-7) док-ся аналог-но соответ-щим св-вам ф-ии а^r.

8) При а>1, При 0<a<1,

Пусть, напр, а>1 и х Пусть М-наперед заданное число. Выберем натур. число N: Тогда 1+N(a-1)>M, а т.к. из нер-ва Бернулли при h=a-1>0 и n=N, имеем: a^N=[1+(a-1)]^N≥1+N(a-1),то и a^N>M, откуда для x>N б. иметь: a^x>a^N>M, и значит

Пусть a>1, но х→-∞. Тогда полагая x=-z и применяя Thy о пределе сложной ф-ии, найдем: т.к. по док-му выше а^z-∞ большая вел-на.

Сл-й 0<a<1 легко привод-ся к разобранным, е/и положить а=1/b.

9) Мн-во знач-й показат-ой ф-ии есть интервал (0,∞).

В с.д., эта ф-я принимает как угодно большие и малые положит-е знач-я, а т.к., кроме того, показ. ф-я непр-на, то она принимает любые знач-я из (0,∞).

Для постр-я графика показ. ф-ии (с а>1) следует учесть: а) у=а^х>0-соответ-щая кривая расположена вся выше оси (ох); б) ф-я у=а^х монот-но возр-т на (-∞,∞), причем -соответ-щая кривая подним-ся неограниченно вверх с возр-ем абсциссы х; в) при х=0 у=а^х=1, т.е. при a>0 соответ-щая кривая проходит ч/з т.А(0,1); г) , т.е. при х→-∞ кривая неограниченно приближ-ся к направленному налево лучу оси (ох), никогда его не достигая (рис. 1). График ф-ии у=а^х при 0<a<1 изображен на рис.2.