Билет №29

1.(1) Степ-ой ф-ей: у = х^μ, где μ- R.

Св-ва:

1) μ=n-N: у = f(x)=xⁿ (1) Опр-е этой ф-ии: у =х для n=1 и у = х∙х∙…∙х для n>1. D(f(x))=(-∞, +∞).

Из def , N-ом k (xⁿ)^k=(x^k)ⁿ=x^nkи (x₁x₂)^k=x₁^k∙x₂^k. При четн n f(x)-чет. ф-я, а при нечет. n-нечет.; при чет. n f(x)>=0.

Иссл f(x) на монть. на [0,∞).

Пусть х₂>x₁≥0. Имеем: f(x₂)-f(x₁)=x₂ⁿ-x₁ⁿ=(x₂-x₁)(x₂^n-1+x₂^n-2x₁+…+x₁^n-1). Т.к. х₂>х₁, то х₂-х₁>0, а т.к. х₂>0 и х₁≥0, то и x₂^n-1+x₂^n-2x₁+…+x₁^n-1>0, f(x₂)-f(x₁)>0 и f(x₂)>f(x₁), т.е. ф-я (1) монотонно возр-т на [0,∞).

Т.к. при чет. n f(x)-чет. ф-я, а при нечет. n-нечет, то на (-∞,0] f(x) монот-но убыв-т при чет n и монот-но возр-т при нечет. n. при чет. n f(x) немонот на (-∞,+∞), а при нечет. n монотонно возр-т на нем. Ч/ы док-ть послед, н/о обнаруж, что и при х₂>0>x₁ имеем: f(x₂)>f(x₁). Но это очевидно: f(x₂)=x₂ⁿ>0, f(x₁)=x₁ⁿ<0 (n-нечет)

2)μ- Z,<0: μ=-m,где m-N.

По def пусть (для х 0): х^-m=1/х^m.Т.о. у=х^-m=1/х^m (2). Обл-тью опр-я ф-ии (2) явл. совокуп-ть 2-х интервалов (-∞,0) и (0,+∞) .Эта ф-я явл. четной при чет. n и нечетной при нечет. n.При чет. n она неотриц-на для х из обл-ти опр-я. Т.к. при положит-х х₁ и х₂ из нер-ва х₂^m>x₁^m 1/х₂^m<1/x₁^m, то из монотон-го возр-я ф-ии(1) на (0,+∞) , что ф-я (2) монотонно убывает на (0, +∞). в интервале (-∞,0) ф-я (2) монотонно убывает при нечет. m и монотонно возр-т при чет. m. График ф-ии (2) для μ= - 2,μ= - 1 изобр-н на рис. 2.

При четном(нечет) m график ф-ии у = х ^{– m} напоминает график ф-ии у = 1/х²(у = 1/х).

3)μ- дробное рац-ое число. Сначало док-м сущ-ние обрат ф-ии у зад на [0,+∞) степ-ой ф-ии х = уⁿ, где n-натур. число. По доказ-му ф-я х = f(y)=yⁿ (1`) монот-на на [0,+∞) и имеет обратную ф-ю у=φ(х)

Т.к. ф-я х=уⁿна [0,+∞) принимает т/о неотриц-ые знач-я, то , что и ф-ии, обратной к (1`), и обл-ть опр-я, и мн-во знач-й есть [0,+∞).Эту обратную ф-ю обозн-т у = (3) и наз. (арифметич-м) корнем n-й ст-ни из х.

Из опр-я обратной ф-ии , что f[φ(x)]=x, т.е. и значит есть число, n-я ст-нь кот. = подкоренному числу х.

Заметим, что т.к. ф-я f(y) монот-но возр-т на [0,+∞), то и обратная ей ф-я у = φ(х)= монот-но возр-т в своей обл-ти опр-я, т.е. на [0,+∞).

Выясним м/о ли построить ф-ю, обратную ф-ии х=уⁿ и в обл-ти отриц-х знач-й х. Е/и n- чет. число, то ф-я х=уⁿ принимает одни лишь неотриц-е знач-я, и ? о построении такой ф-ии отпадает, так что, при чет. n записью у= представлена ф-я, обратная к (1), то в этой записи х≥0.

При n-нечет. ф-я х=уⁿ, рассм-ая на (-∞,+∞), монот-на уже во всем этом интервале, причем х<0 при у<0, п.э. она имеет обрат. ф-ю с обл. опр-я (-∞, +∞). Эту обрат.ф-ю тоже обоз-т ч/з у = (3`) и наз. корнем n-й(нечет) ст-ни из х.

Мн-во знач-й этой ф-ии есть интервал(-∞,+∞); она б. монот-но возр-щей в (-∞,+∞). При и х₁≥0, х₂≥0:

Определим теперь ф-ю у= х^μ для дробного полож-го рац-го показ-ля μ=r.

рац-ое полож-ое число r м.б. представлено r = . По опр-ю полагают: (4)

При таком опр-ии кажд. х, при кот. , сопоставл-ся !-ое число у, и здесь у есть ф-я от х. Ее и наз. степ-ой ф-ей с положит-м рац-ным показателем.

Установим обл-ть сущ-ния ф-ии(4). При нечет. n ф-я (3`) опред-на на (-∞, +∞), п.э. при нечет. n и ф-я (4) имеет обл. сущ-ния интервал (-∞,+∞). Е/и n-нечет. число, то m-нечетно. Но ф-я (3) при чет. n опр-на т/о при неотриц-х знач-ях подкоренного выр-я. Значит в (4) д.б. x^m≥0 (m-нечетно), х≥0, т.е. при чет. n обл. сущ-ния ф-ии(4) есть [0,+∞).

При чет. m (n нечетно) ф-я (4)явл. четной: а при нечет. m и нечет. n-нечетной:

Исслед. теперь ψ(х) на монот-ть на [0,+∞). Выше б. показано, что ф-я х^m при натур.m монот-но возр-т на [0,+∞), так что е/и z₂=x₂^m, z₁=x₁^m,то при х₂>x₁≥0 и z₂>z₁≥0. Но ф-я у= монот-но возр-т на[0,+∞), п.э. при z₂>z₁≥0 и при х₂>x₁≥0 ψ(х) монот-но возр-т на [0,+∞). Е/и n четно, то ф-я (4)опр-на т/о на этом полусегменте, и п.э. при чет. n дальн-го исслед-я этой ф-ии на монот-ть проводить не надо. Пусть теперь n-нечет. Тогда ф-я (4) опр-на и на (-∞,0] и м/о проводить дальн. ее исслед-е на монот-ть.

Е/и и m –нечет., то ф-я (4) нечетна и значит монот-но возр-т и на (-∞,0]; е/и m-чет., то эта ф-я четна и монот-но убывает на (-∞,0].; при n нечет. и m чет. ф-я (4) не монот-на в (-∞,+∞), тогда как при n нечет.,m-нечет. она монот-но возр-т во всем (-∞,+∞). На рис.3 изображены графики ф-й у=х^r для r=1,1/2,1/3,2/3.

Е/и r- есть отриц-ое рац-ое число, то у = Положим r=m/n,где m,n-взаимно простые натур числа. Ф-я Ψ₁(х) опр-на всюду, где опр-на ф-я х^|r|, кроме х=0, п.э. имеет своей обл. сущ-ния(0,+∞) при чет. n и совокуп-ть 2-х интервалов (-∞0) и (0,+∞) при нечет. n.

При r=0 cтеп. ф-я принимает вид: у = х⁰. При х=0 такая ф-я не опр-на, а для ост-х знач-й аргум-та она ≡ с ф-ей у=1.

Итак, для всех рац-х знач-й r построена и рассм-на степ. ф-я у = х^r. Из сказ-го выше , что эта ф-я при рац-ном r монот-на на (0, +∞): монот-но возр-т при r>0 и монот-но убыв-т при r<0.

Cв-ва ст-ней: е/и а>0,b>0; r Q,s Q, тогда справ-во:

1. (а^r)^s=a^rs ; 2) a^r∙a^s=a^r+s ; 3) a^r∙b^r=(ab)^r.

Док-во 1): Пусть r Q,s=p N тогда обозн. ч/з r=m/n,тогда (a^r)^s=(a^m/n)^p=a^mp/n=a^rs. Рассм. сл-й, когда s=p/q, q N; c₁=(a^m/n)^p/q , c₂=a^mp/nq , методом от прот –го допустим с₁ с₂,c>c₁, c₂<c₁

c₁^q c₂^q a^mp/n a^mp/n это противоречит тому, что s=p N. ч.т.д.

Док-во2):

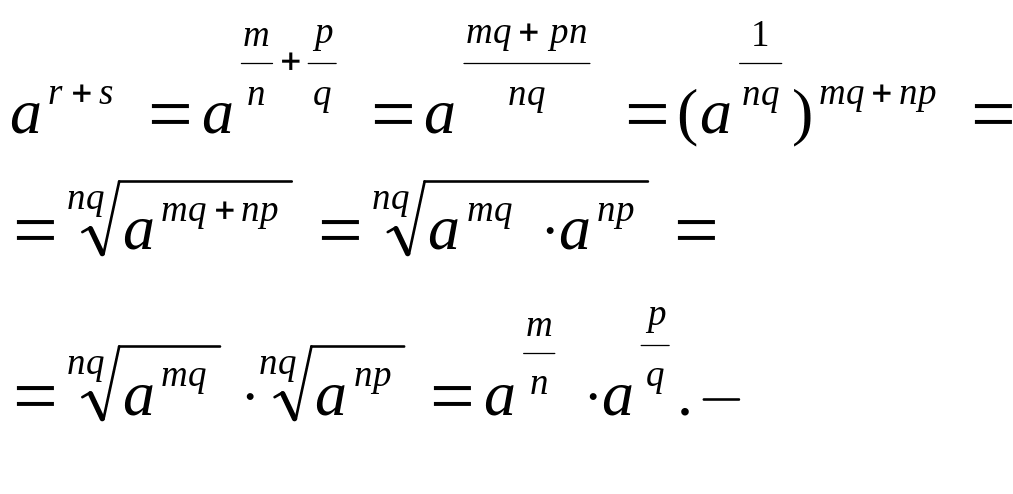
(Степенная функция с произвольным показателем)Введем степенную ф-ию с иррац-ым показателем α: y = f(x)= x^α.

Знач-е этой ф-ии в точке х = а>0 опред-ся как знач-е φ(α) показат. ф-ии φ(х) = а^х в точке х=α. Для х=0 полагаем, по опр-ю, для α >0:f(0)=0^α=0; для отриц-х же знач-й х мы эту ф-ю не определяем. Т.о. обл-ть ее опр-я – полусегмент [0,+∞], е/и α>0 и интервал (0, +∞), е/и α<0.

При х = а>0 f(а)=φ(α)=а^α>0, т.е. на интервале (0,+∞) f(х) принимает т/о положит. знач-я.

Ч/ы подвергнуть степ. ф-ю дальн. исслед-ю (на монотонность и непр-ть), удобно восп-ся приемом представл-я ф-ии в виде показат. ф-ии.

Исходя из тожд-ва а^{loga x}= x(х>0), м/о записать в силу нер-ва х^α>0(для х 0): х^α = е^{ln x} ,т. е. y = f(x)=x^α=e^{ln x} (0<x<∞)(1) или y = e^u, где u= αln x (2).

Пусть теперь х₂>x₁>0, тогда в силу монотонного возрастания ф-ии ln x (e>1) и ln x₂> ln x₁. Отсюда при α>0 (α<0) имеем: α ln x₂> α ln x₁ (α ln x₂<α ln x₁), а т.к. показат. ф-я е^u также монотонно возрастает, то и e^{α ln x} > e^{α ln x} (e^{α ln x} < e^{α ln x} ), или по (1): х^α₂>х^α₁ (х^α₂< х^α₁), т.е.f(x₂)>f(x₁) [f(x₂)<f(x₁)].

Т.о. степ. ф-я y = f(x)=x^α на интервале (0, ∞) монотонно возрастает при α>0 и монотонно убывает при α<0.

Исследуем f(x)на непр-ть. Будем исходить из (2).

Ф-я u = α ln x непр-на на (0, +∞); непр-ой в кажд. точке u явл. и ф-я е^u. отсюда по теореме о непр-ти сложной ф-ии ф-я y = e^{α ln x} , т.е. ф-я y = f(x)=x^α непр-на на интервале (0, +∞).

2.Показательная функция. Её основные свойства.

Показат. ф-я имеет вид: у=а^х,(*) где постоянная а полож-на (а 1).

Отметим ее осн. св-ва:

1. Ф-я (*) полож-на для х; ее обл-ть знач-й – интервал (0,+∞).

2. При а (a>0,a 1) у_х=0=1.

3. При х>0 y>1 для a>1 и y<1 для a<1; при х<0 рез-ты обращ-ся.

4. При a>1 ф-я монот-но возр-ет, а при a<1-монот-но убыв-т вовсей своей обл-ти опр-я.

График ф-ии (*) представлен на рис. 1. для а>1, и на рис. 2. для a<1.