Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a = b = c .

sinA sinB sinC

Теорема косинусов.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. a²=b² + c² – 2bc cosA.

Теорема: В любой треугольник можно вписать окружность, причём единственным образом; центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника. (центр вписанной в треугольник окружности всегда лежит внутри треугольника).

Теорема: около любого треугольника можно описать окружность, причём единственным образом; центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника. (Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника; центр окружности, описанной около тупоугольного треугольника лежит вне треугольника; центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы треугольника).

Площадь треугольника.

1)S=1/2 ah_a – площадь треугольника равна половине произведения его основания на высоту.

2)S=1/2 ab sinC – площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

3) – формула Герона.

4)S= r p

5)

a, b, c – длины сторон треугольника.

p=a + b + c

2

r – радиус вписанной окружности.

R – радиус описанной окружности.

Свойства равнобедренного треугольника.

Теорема: В равнобедренном треугольнике углы при основании равны; биссектриса, проведённая к основанию является медианой и высотой.

Свойства прямоугольного треугольника.

1)Сумма 2 острых углов прямоугольного треугольника равна 90.

2)Катет прямоугольного треугольника, лежащий против угла в 30 равен половине гипотенузы.

Признаки равенства прямоугольных треугольников.

1)Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

2)Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

3)Если катеты одного прямоугольного треугольника соответственно равны катетам другого, такие треугольники равны.

4) Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

Соотношения между сторонами и углами прямоугольного треугольника.

Т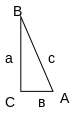 еорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. c²=a² + b² . Если взять равнобедренный прямоугольный треугольник с катетом a, то

по теореме Пифагора получим c² = a² + a² => c² = 2a² => c = => c = a , т.е.

гипотенуза прямоугольного равнобедренного треугольника в раз больше катета.

Площадь прямоугольного треугольника равна половине произведения его катетов.

Определение: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе sinA = a/c => a = c sinA – катет прямоугольного треугольника равен гипотенузе, умноженной на синус противолежащего катету угла.

Определение: Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе cosA = b/c => b = c cosA - катет прямоугольного треугольника равен гипотенузе, умноженной на косинус прилежащего катету угла.

Определение: Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему tgA = a/b => a = b tgA - катет прямоугольного треугольника равен другому катету, умноженному на тангенс угла, противолежащего искомому катету.

Определение: Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему ctgA = b/a => b = a ctgA - катет прямоугольного треугольника равен другому катету, умноженному на котангенс угла, прилежащего искомому катету.

	30	45	60
sin
cos
tg		1
ctg		1