Методы последовательного приближения

Существуют различные методы последовательных приближений при отыскании действительных корней уравнений на промежутке, на котором выполнены условия отделимости корней.

Метод половинного деления

Метод половинного деления называют еще методом деления отрезка пополам или методом дихотомии. По своей идее метод прост, так как не требует выполнения ограничивающих условий для первой и второй производных, но его реализация связана с длительными вычислениями (большим числом итераций).

Пусть известно, что на отрезке находится один действительный корень уравнения , следовательно, . Надо определить этот корень с заданной точностью .

Суть метода состоит в том, что отрезок делим пополам точкой (первое приближение) и рассматриваем тот из отрезков или , который содержит искомый корень. Обозначив этот отрезок через , причем , определяем точку (второе приближение) и рассматриваем отрезок или , содержащий искомый корень, т.е. , где , и т. д. до тех пор, пока не получим отрезок , содержащий искомый корень , для которого

.

Точку принимаем за приближенное значение корня , при этом очевидно, что .

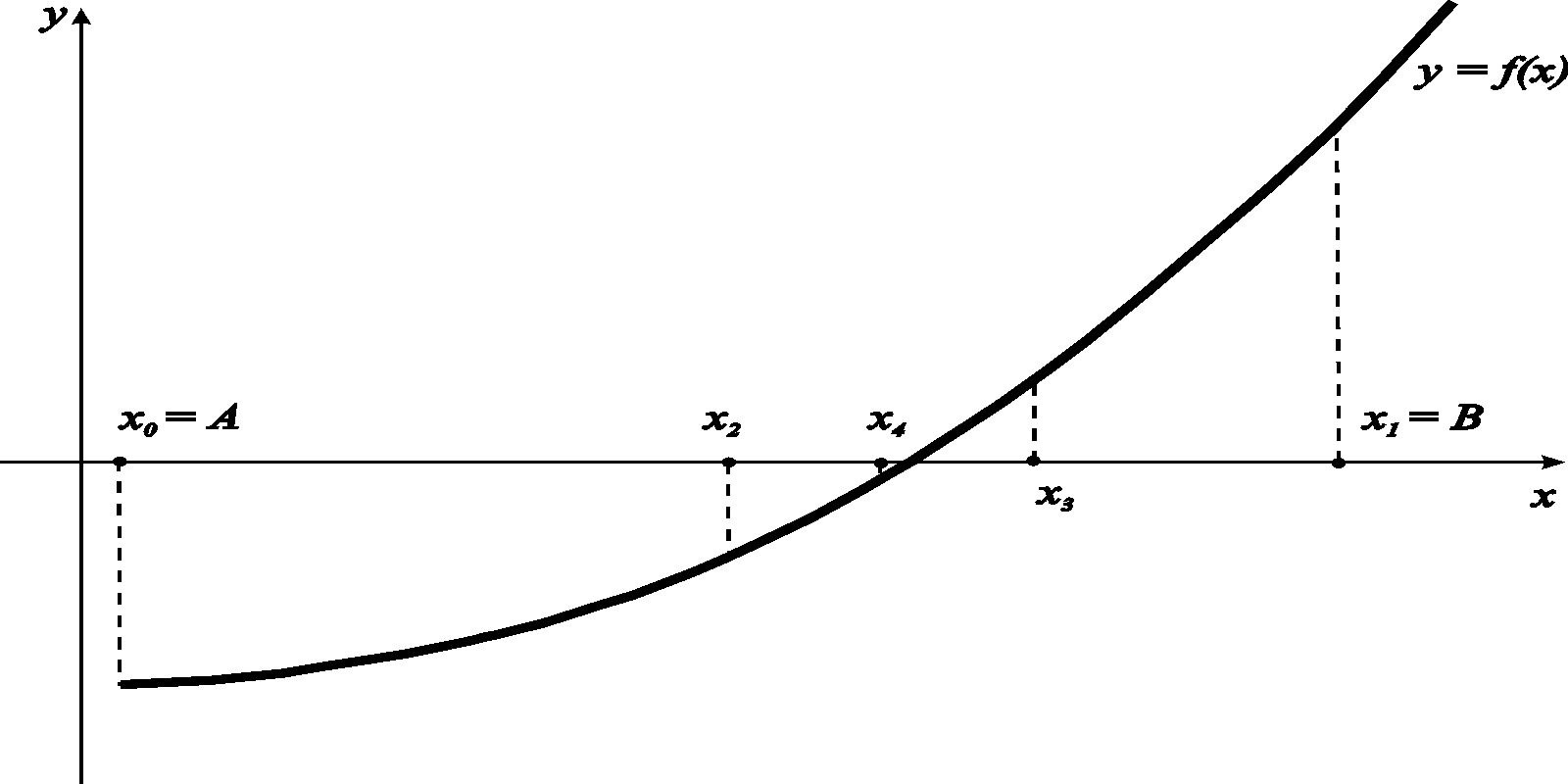
Алгоритм. Пусть известен отрезок , для которого , и уравнение имеет на этом отрезке только один корень (выполнение условий 2), 3) отделения корня для этого метода не обязательно), задана точность приближения к корню .

1. Обозначим , , .

2. Пусть определен отрезок .

Находим . Вычисляем .

3. Если , то – корень заданного уравнения.

В противном случае определяем знак произведения .

4. Если , то обозначаем , и переходим к действию 5.

Если , то обозначаем , и переходим к действию 5.

5. Если , то – корень заданного уравнения, в противном случае полагаем и переходим к действию 2.

Метод простых итераций

Рассмотрим уравнение

.

Пусть известно, что на отрезке находится единственный корень уравнения , то есть , и на этом отрезке выполняются все условия отделимости корня. Требуется определить этот корень с заданной точностью .

Вместо заданного уравнения рассмотрим эквивалентное уравнение

,

которое получается из заданного следующими преобразованиями

, где , ,

,

тогда .

Полученное эквивалентное уравнение имеет этот же корень , то есть выполняется равенство , а – отрезок, отделяющий корень этого уравнения.

Выбираем произвольную точку и первым приближением к решению назовем число , где , по первому приближению строим второе и т.д.

,

Таким образом строится последовательность приближений

Если полученная последовательность сходится, причем

,

то за конечное число итераций будет получено приближение , представляющее приближенное значение корня с заданной точностью

.

Выясним вначале геометрический смысл процесса и его сходимости.

Корень уравнения – это абсцисса точки пересечения прямой и графика функции . Точка – произвольная точка промежутка , – абсцисса точки – точки пересечения прямых и . По определяем – абсциссу точки – точки пересечения прямых и и т. д. На следующих рисунках показана последовательность , которая сходится к корню уравнения.

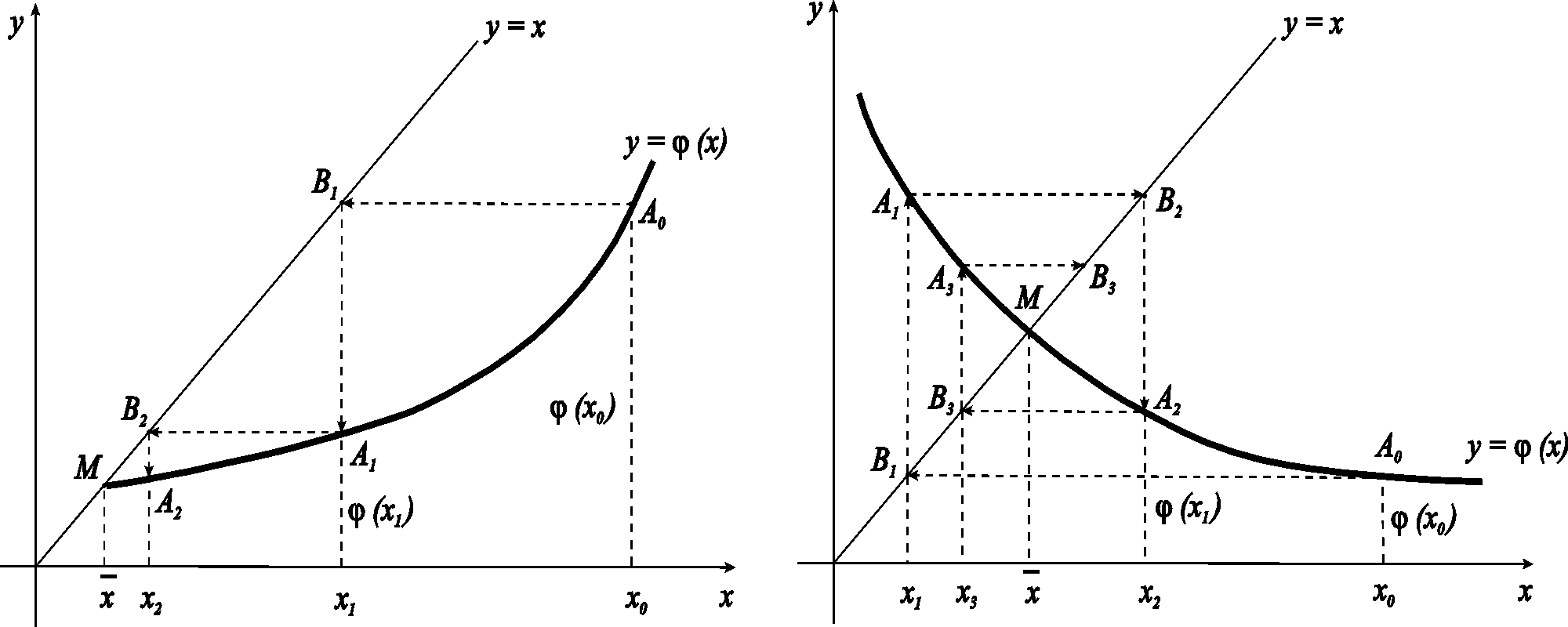
Установим условия сходимости метода. Поскольку – точное значение корня уравнения, то , а построенная последовательность строится по формуле , тогда

,

где , а . Последовательно применяя полученное соотношение, приходим к неравенству

,

которое в пределе принимает значение

при условии, что . В этом случае получаем, что построенная последовательность стремится к решению уравнения .

Условие сходимости метода можно выполнить за счет выбора значения параметра , входящего в выражение для функции . Получаем, что

для всех или

для всех ,

или .

При выбираем из условия .

При выбираем из условия .

Если функция имеет на ограниченную производную , то при выбираем , при выбираем . При этом выполняются условия сходимости метода простой итерации для заданного уравнения .

Алгоритм. Пусть на отрезке отделен корень уравнения и задана точность вычислений .

1. Заменяем уравнение на эквивалентное и выбираем так, чтобы было выполнено условие . Выбираем .

2. Пусть определено -ое приближение . Вычисляем

3. Если , то корень уравнения найден . Если же , то полагаем и переходим к шагу 2.

Пример. Уравнение преобразовать к виду, допускающему применение метода итераций. Известно, что корень отделен на отрезке [1; 2].

Решение. Преобразуем уравнение к виду .

Тогда . Выберем так, чтобы для всех . Имеем . Отсюда . Решая это неравенство, получаем

, .

Так как при функция ограничена, то , . Пусть , тогда строим сходящуюся к решению последовательность .