6.Численное решение краевых задач для уравнений математической физики

6.1.Характеристика метода конечных разностей для решения уравнений математической физики

Метод конечных разностей, или метод сеток, является одним из самых распространенных методов численного решения краевых задач для уравнений математической физики, которые описываются дифференциальными уравнениями второго порядка в частных производных. В основе метода лежит идея замены частных производных соответствующими конечно-разностными отношениями.

Мы ограничимся рассмотрением неизвестных функций, зависящих от двух независимых переменных. Пусть в плоскости имеется некоторая область с границей . Построим на плоскости два семейства параллельных прямых:

,

.

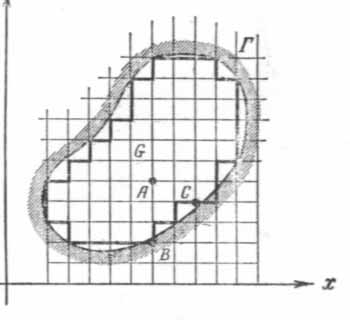
Точки пересечения этих прямых назовем узлами сетки.

Два узла называются соседними, если они удалены друг от друга в направлении оси или на расстояние, равное шагу сетки или соответственно.

Выделим узлы, принадлежащие области , а также некоторые узлы, не принадлежащие этой области, но расположенные на расстоянии, меньшем, чем шаг, от границы .

Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними (узел А). Оставшиеся из выделенных узлов называются граничными (узлы В, С).

Значения искомой функции в узлах сетки будем обозначать через . В каждом внутреннем узле , где , заменим частные производные первого порядка центральными конечно-разностными отношениями:

, ,

в граничных точках мы вынуждены пользоваться менее точными формулами

, ,

Аналогично заменяются частные производные второго порядка

, .

Указанные замены производных в каждом узле сетки позволяют свести решение уравнений в частных производных к решению системы разностных уравнений.

6.2.Метод конечных разностей решения задачи дирихле в прямоугольной области

Рассмотрим краевую задачу для дифференциального уравнения в частных производных второго порядка, относящегося к эллиптическому типу.

Задача Дирихле заключается в нахождении функции , удовлетворяющей внутри некоторой заданной области уравнению Пуассона

или уравнению Лапласса

а на границе области граничным условиям

,

где – заданная непрерывная функция.

Рассмотрим сначала прямоугольную область изменения переменных , а граничные условия зададим на каждой стороне прямоугольной области:

, , ,

, , .

Для решения краевой задачи применим метод конечных разностей. Для этого в области построим два семейства параллельных прямых, проходящих через точки , на осях координат, где , .

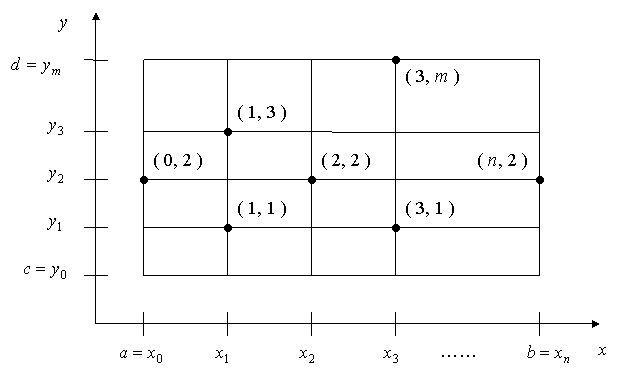
Значения неизвестной функции в узлах сетки обозначим через , , .

Значения искомой функции в граничных точках определим из заданных граничных условий.

Граничное условие

,

выполняется для и всех , где : ,

или

, .

Граничное условие

,

выполняется для и всех , где : ,

или

, .

Граничное условие

,

выполняется для и всех , где : ,

или

, .

Граничное условие

,

выполняется для и всех , где : ,

или

, .

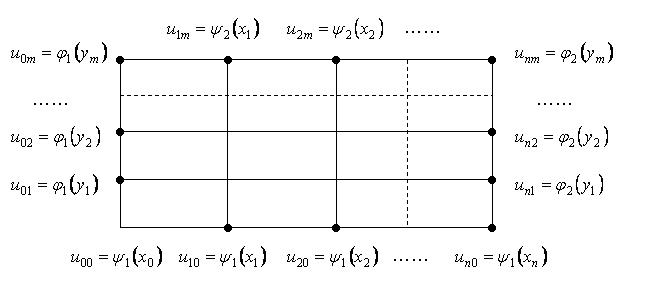
Значения искомой функции во внутренних точках области определим из заданного уравнения, заменив производные их выражениями через конечные разности

, .

При этом вместо дифференциального уравнения в частных производных получим соответствующее конечно-разностное уравнение

для уравнения Пуассона и

для уравнения Лапласса.

Полученные уравнения справедливы для всех , и вместе с граничными условиями образуют систему линейных алгебраических уравнений относительно значений функции во внутренних узлах сетки, а значения в граничных узлах в точности равны значениям заданных граничных функций.

В каждом таком уравнении задействованы значения искомой функции в узлах, определяемых следующей схемой.

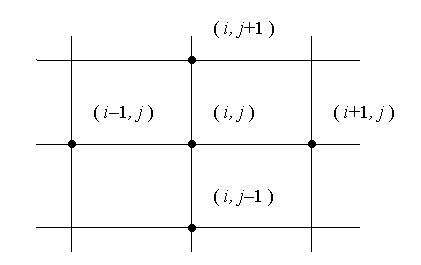
Наиболее простой вид эта система получает, если шаг разбиения области вдоль оси ОХ будет равен шагу разбиения области вдоль оси ОУ

.

В этом случае конечно-разностные уравнения примут вид:

для уравнения Пуассона и

для уравнения Лапласа, если , .

Погрешность замены дифференциального уравнения конечно-разностным оценивается величиной

, где .

Однако погрешность приближенного решения, полученного конечно-разностным методом, складывается на трех видов погрешностей:

1. погрешности замены дифференциального уравнения конечно-разностным;

2. погрешности аппроксимации краевых условий;

3. погрешности, получаемой в результате того, что система конечно-разностных уравнений решается приближенным методом.

Пример. Рассмотрим задачу о стационарном распределении тепла в плоской квадратной изолированной пластине со стороной, равной 1, если на границе пластинки поддерживается постоянная температура.

Известно, что функция , задающая распределение температуры в пластине, является решением уравнения Лапласса

.

Значения функции в граничных точках области показаны на рисунке.

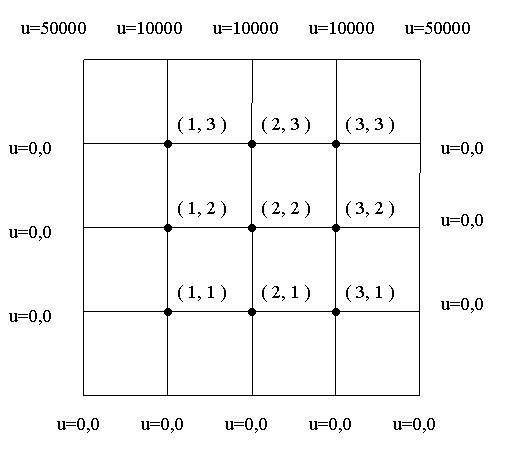
Решение. Построим сетку с шагом . Получим девять внутренних узлов, в которых необходимо определить значение функции. Для этих узлов запишем конечно-разностные уравнения.

В силу симметрии граничных условий имеем

,

что сокращает число неизвестных значений функции и во внутренних узлах до шести. Таким образом, в узлах (3, 1), (3,2), (3, 3) конечно-разностиые уравнения писать не нужно. А для остальных шести внутренних узлов (1, 1), (2, 1), (1,2), (2,2), (1,3), (2, 3) получаем соответственно шесть уравнений:

Кроме неизвестных значений во внутренних узлах в эти уравнения входят еще 12 значений функции в граничных точках. Эти значения следует взять из краевых условий

Заметим, что в остальных узлах граничные условия не используются. Окончательно, система уравнений примет вид

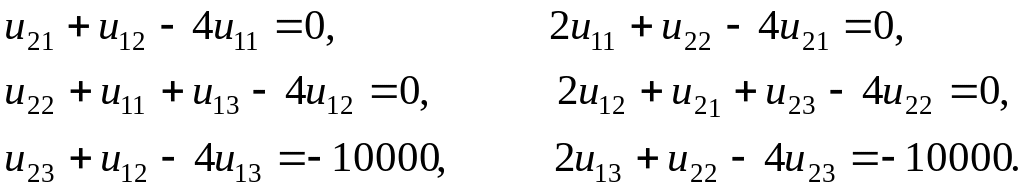
Решив эту систему методом Гауса, получим

.