6.5.Метод конечных разностей для решения уравнений гиперболического типа
Рассмотрим краевую задачу для дифференциального уравнения в частных производных второго порядка гиперболического типа. Задача заключается в нахождении функции , удовлетворяющей уравнению
начальным условиям
и граничным условиям
.
Если , то рассматривается краевая задача для неоднородного уравнения, если – краевая задача для однородного уравнения.
Сформулированная задача, в частности, описывает колебания струны, функция определяет положение каждой точки струны в момент времени . Начальные условия для каждой точки струны описывают начальное положение и начальную скорость. Граничные условия описывают изменение положения граничных точек струны и с течением времени. Функция определяет наличие возбуждающих сил, действующих на струну.
Для решения краевой задачи применим метод конечных разностей. Для этого в области построим два семейства параллельных прямых, проходящих через точки , на осях координат. Значения неизвестной функции в узлах сетки обозначим через , ,
Для нахождения значений искомой функции на границах заданной области воспользуемся заданными краевыми условиями.
Из граничных условий
следует
,
Из первого начального условия
следует
, .
Остановимся подробнее на втором начальном условии
,
которое выполняются для и всех , где :
,
.
Частную производную по времени представим через соответствующую конечную разность
,
,
откуда следует, что
,
.
Полученная формула позволяет вычислить
значения искомой функции при
.
Итак, начальные условия позволяют
вычислить значения функции на первых
двух слоях сетки.
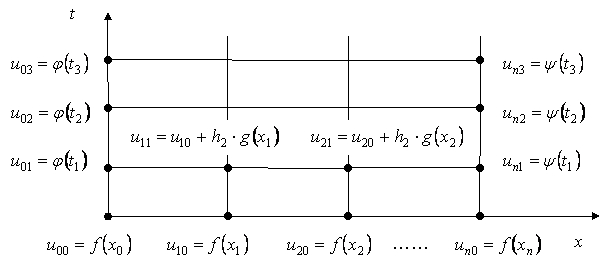
Все остальные значения получаем из уравнения, заменой в нем частных производных соответствующими выржениями через конечные разности при ,
После умножения уравнения на
получим
,
,
Обозначив
,
приводим эти уравнения к виду
,
,
Заметим, что в полученном равенстве
используется явная схема узлов, так как
позволяет найти значения функции
на слое
,
если известны значения на двух предыдущих
слоях.
Два начальных условия дали возможность найти приближенноые значения искомой функции на двух начальных слоях сетки, что позволяет использовать полученное равенство для нахождения значений функции, начиная со второго слоя при .
Доказано, что при
полученное разностное уравнение
устойчиво.
В частности, при
равенство имеет наиболее простой вид:
,
,
Оценка погрешности приближенного решения, полученного из конечно-разностного уравнения в полосе , имеет вид
Пример. Найти приближенное решение уравнения
,
удовлетворяющего условиям
,
,
, 
.
Решение. Будем использовать
конечно-разностное равенство при
.
Выберем по аргументу
шаг
.
Так как
,
получаем по аргументу
шаг
.
Разобъем промежуток
на части точками деления
,
а промежуток
точками
Тогда
; ; ; ; ; .
;
;
;
;
;
.
Воспользуемся первым начальным условием и определим значения функции на нулевом слое по формулам:
; , .
Получим
; ;
; ;
; .
Воспользуемся вторым начальным условием и определим значения функции на первом слое по формулам:
; 
,
.
Получим
; 
; 
;
; 
; 
.
Воспользуемся граничными условиями и определим значения функции на левой и правой границах области по формулам:
;
; 
;
; ; .
Вычисляем значения
на последующих слоях
по формуле
, 
.
При
для
последовательно получаем
;
;
;
;
и т.д.
В результате получим следующие значения:
10 |
2 |
|
0 |
0,5878 |
0,9511 |
0,9511 |
0,5878 |
0 |
9 |
1,8 |
|
0 |
0,3633 |
0,5878 |
0,5878 |
0,3633 |
0 |
8 |
1,6 |
|
0 |
0 |
0 |
0 |
0 |
0 |
7 |
1,4 |
|
0 |
-0,363 |
-0,588 |
-0,588 |
-0,363 |
0 |
6 |
1,2 |
|
0 |
-0,588 |
-0,951 |
-0,951 |
-0,588 |
0 |
5 |
1 |
|
0 |
-0,588 |
-0,951 |
-0,951 |
-0,588 |
0 |
4 |
0,8 |
|
0 |
-0,363 |
-0,588 |
-0,588 |
-0,363 |
0 |
3 |
0,6 |
|
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0,4 |
|
0 |
0,3633 |
0,5878 |
0,5878 |
0,3633 |
0 |
1 |
0,2 |
|
0 |
0,5878 |
0,9511 |
0,9511 |
0,5878 |
0 |
0 |
0 |
|
0 |
0,5878 |
0,9511 |
0,9511 |
0,5878 |
0 |
j |
t |
|
|
|
|
|
|
|
|
|
x |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
i |
0 |
1 |
2 |
3 |
4 |
5 |