Графический метод отделения корня

Графически корни уравнения можно отделить, построив график функции и приблизительно определив точки его пересечения с осью . Однако задача построения графика не всегда простая. Обычно уравнение

заменяют эквивалентным уравнением

, где , или

,

подбирая функции и так, чтобы строить их графики было проще, чем график функции . Абсциссы точек пересечения графиков и будут искомыми корнями заданного уравнения.

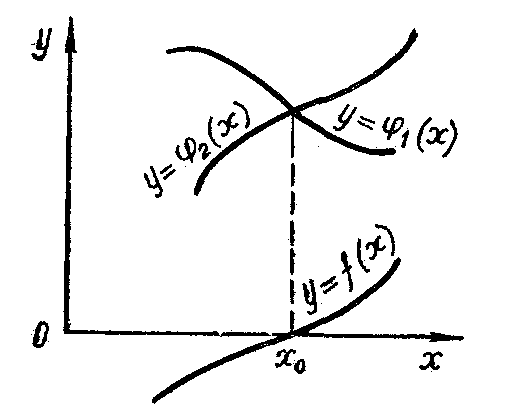
Пример 1. Отделить графическим методом корни уравнения

.

Решение. Перепишем данное уравнение в виде

и рассмотрим две функции и . Построим графики этих функций и определим абсциссы точек их пересечения.

Как видно из рисунка, заданное уравнение имеет два действительных корня (графики пересекаются в двух точках), причем один из корней отрицательный, а второй — положительный. Оба корня по абсолютной величине не превосходят , а именно и .

Отделение корней методом проб

Этот метод состоит в том, что наугад выбирают точку из области определения функции (либо из более узкой области), находят знак , а затем подбирают точку так, чтобы значение функции имело знак, противоположный знаку . Далее определяют знак внутри отрезка . Если не меняет знака на , то корень отделен, в противном случае отрезок сужают, взяв точку , лежащую посредине отрезка . Определяют знак и в качестве нового отрезка рассматривают либо (если ), либо (если ). Обозначив новый отрезок через , повторяют те же действия, что и на отрезке , до тех пор, пока не будет найден отрезок , отделяющий корень.

Пример 2. Методом проб отделить положительный корень уравнения

.

Решение. Функция определена на всей числовой прямой. Поскольку требуется отделить положительный корень уравнения, рассмотрим полуинтервал .

1. Находим . Затем выбираем любую точку, например , и вычисляем . Так как , то ничего определенного об отрезке сказать нельзя. Надо подобрать так точку , чтобы было , а для этого должно быть больше, чем . Возьмем, например, , тогда , а следовательно, па отрезке есть корень, .

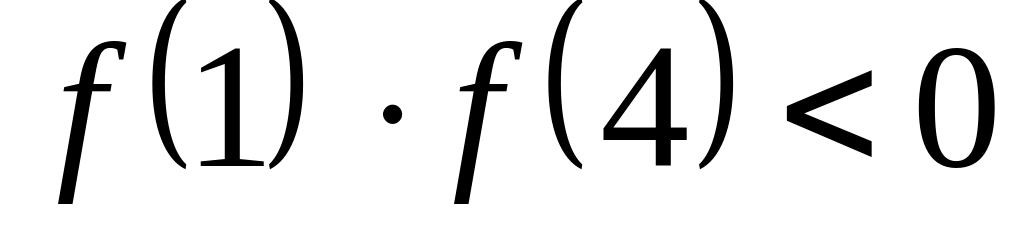2. Поскольку , то непосредственной проверкой убеждаемся, что на отрезке производная меняет знак, так как и .

Сужаем отрезок . Возьмем, например, точку . Тогда и . Следовательно, на отрезке есть корень. Проверяем знак . Имеем , а для , очевидно, производная возрастает, поэтому остается положительной. Таким образом, корень отделен. На отрезке находится положительный действительный корень заданного уравнения.

3. Заметим, что для всех .

Функция на промежутке удовлетворяет всем условиям отделимости корней.

Метод выделения интервалов монотонности

Этот метод состоит в том, что вначале определяем интервалы монотонности функции (если это не сложно), т. е. интервалы области определения функции, в которых сохраняет знак. Затем вычисляем знаки на концах этих интервалов и определяем интервал , на котором сохраняет знак и . Задача отделения корня выполнена. Таким способом можно отделить все действительные корни уравнения .

Если же среди интервалов монотонности функции не существует интервала, на концах которого функция имеет разные знаки, то это означает, что либо уравнение не имеет действительных корней, либо таковыми являются границы интервалов монотонности, т. е. для этих точек и . Это уже так называемые кратные корни.

Пример 3. Отделить действительные корни уравнения

.

Решение. Рассматриваем функцию , которая определена на всей числовой прямой.

1. Находим первую производную и интервалы монотонности функции. Получаем

,

откуда

, ,

так что интервалами монотонности функции являются все интервалы вида

.

2. Определяем знаки функции в граничных точках интервалов монотонности. Взяв отрезок , находим

, .

и убеждаемся, что на этом отрезке есть один корень уравнения. По виду функции заключаем, что для будет (так как и ), а для будет (так как и ). Следовательно, в остальных интервалах монотонности функция знака не меняет. Уравнение имеет единственный корень, который находится на отрезке .

3. Учитывая третье условие, находим вторую производную , которая на отрезке меняет знак. Поэтому отрезком, отделяющим корень, будет , поскольку

1. , , ;

2. не меняет знака на ;

3. не меняет знака на .

Функция на промежутке удовлетворяет всем условиям отделимости корней.